群体智能算法-黏菌寻找食物最优路线行为模拟 2
经过查找一些资料,发现目前比较好的理论支撑有元胞自动机,其中的分形理论中的扩散限制凝聚模型与黏菌的网络比较贴切。
经过反复的调整。现在购机了一个黏菌的网络。如图:
第一个图为模拟的过程
第二图为最终图的放大

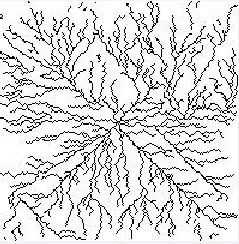
其中依然有有几个假设
1、黏菌的生命力,随着扩展,生命力降低
2、随着扩展完之后,黏菌在整个扩展范围内,随机生成一些感触点,然后感触点生成网络
感触点的生长原则,则是最大可能从生命力低的地方向生命力高的地方生长,直至生长到了有网络的地方,或者是黏菌的核心。
不足的地方:
在模拟行为中采用的是元胞为小方块,所以会出现图中的一些对角线的直线。
备注:
其中图片采用的是jpg,为200*200像素。加载的是一个全白的图片,后面的黑点为程序模拟出来的
源码如下
龚浩华
qq 29185807 月牙寂
2015年4月1日
经过反复的调整。现在购机了一个黏菌的网络。如图:
第一个图为模拟的过程
第二图为最终图的放大


其中依然有有几个假设
1、黏菌的生命力,随着扩展,生命力降低
2、随着扩展完之后,黏菌在整个扩展范围内,随机生成一些感触点,然后感触点生成网络
感触点的生长原则,则是最大可能从生命力低的地方向生命力高的地方生长,直至生长到了有网络的地方,或者是黏菌的核心。
不足的地方:
在模拟行为中采用的是元胞为小方块,所以会出现图中的一些对角线的直线。
备注:
其中图片采用的是jpg,为200*200像素。加载的是一个全白的图片,后面的黑点为程序模拟出来的
源码如下
package main
import (
"fmt"
"image"
"image/jpeg"
//
"io"
"image/color"
"math/rand"
"os"
"path"
"runtime"
"sync"
"time"
)
func main() {
runtime.GOMAXPROCS(1)
for {
select {}
}
}
var max_x int = 200
var max_y int = 200
var lock *sync.RWMutex
var im image.Image
var AllPart []Parts
var wg *sync.WaitGroup
type Parts []*Part
type Part struct {
x int
y int
en int
black bool
walked bool
}
func NewPart(x, y int) *Part {
p := Part{x, y, 0, false, false}
return &p
}
func initImage() error {
f, err := os.Open("200.jpg")
if err != nil {
fmt.Println(err)
return err
}
defer f.Close()
im, err = jpeg.Decode(f)
if err != nil {
fmt.Println(err)
return err
}
return nil
}
func Print() {
tick := time.Tick(1 * time.Second)
count := 1
for {
select {
case <-tick:
func() {
p := path.Join("./worm", fmt.Sprintf("%d.jpg", count))
lock.Lock()
f, _ := os.OpenFile(p, os.O_RDWR|os.O_CREATE, 0x666)
jpeg.Encode(f, im, nil)
f.Close()
lock.Unlock()
count++
}()
}
}
}
func init() {
initImage()
wg = &sync.WaitGroup{}
lock = &sync.RWMutex{}
AllPart = make([]Parts, max_y, max_y)
for y := 0; y < max_y; y++ {
AllPart[y] = Parts(make([]*Part, max_x, max_x))
}
for y := 0; y < max_y; y++ {
for x := 0; x < max_x; x++ {
AllPart[y][x] = NewPart(x, y)
}
}
AllPart[max_y/2][max_x/2].en = 200
AllPart[max_y/2][max_x/2].black = true
AllPart[max_y/2][max_x/2].walked = true
SetBlack(max_x/2, max_y/2)
for i := 0; i < 500; i++ {
rand.Seed(rand.Int63())
y1 := int(rand.Int31()) % max_y
x1 := int(rand.Int31()) % max_x
if x1 == max_x/2 && y1 == max_y/2 {
continue
}
AllPart[y1][x1].black = true
SetBlack(x1, y1)
}
for y := 0; y < max_y; y++ {
for x := 0; x < max_x; x++ {
wg.Add(1)
}
}
for y := 0; y < max_y; y++ {
for x := 0; x < max_x; x++ {
go AllPart[y][x].run()
}
}
go Print()
}
func getEn(x, y int) int {
if x < 0 || y < 0 {
return -1
}
if x >= max_x || y >= max_y {
return -1
}
return AllPart[y][x].en
}
func SetBlack(x, y int) {
p := im.(*image.YCbCr)
if !(image.Point{x, y}.In(p.Rect)) {
return
}
yi := p.YOffset(x, y)
ci := p.COffset(x, y)
p.Y[yi], p.Cb[ci], p.Cr[ci] = color.RGBToYCbCr(0, 0, 0)
}
func (p *Part) run() {
wg.Done()
wg.Wait()
tick := time.Tick(1 * time.Second)
for {
select {
case <-tick:
if p.walked {
return
}
func() {
other := make(map[*Part]int)
max_node := 0
otherblack := 0
getmax := func(xi, yi int) {
en := getEn(xi, yi)
if en > 0 {
other[AllPart[yi][xi]] = en
if AllPart[yi][xi].black {
otherblack++
}
}
if en > max_node {
max_node = en
}
}
getmax(p.x-1, p.y-1)
getmax(p.x, p.y-1)
getmax(p.x+1, p.y-1)
getmax(p.x-1, p.y)
getmax(p.x+1, p.y)
getmax(p.x-1, p.y+1)
getmax(p.x, p.y+1)
getmax(p.x+1, p.y+1)
if p.en == 0 {
if max_node > 0 {
p.en = max_node - 1
}
return
}
if p.black {
//maxwalk
ensum := 0
havewalked := 0
nextother := make(map[*Part]int)
for np, en := range other {
if en > p.en {
nextother[np] = en
ensum += en
if np.walked {
havewalked++
}
}
}
if len(nextother) <= 1 {
for np, en := range other {
if en == p.en {
nextother[np] = en
ensum += en
if np.walked {
havewalked++
}
}
}
}
if len(nextother) == 0 {
for np, en := range other {
if en < p.en {
nextother[np] = en
ensum += en
if np.walked {
havewalked++
}
}
}
}
if havewalked > 0 {
p.walked = true
return
}
if ensum > 0 {
rand.Seed(rand.Int63())
rn := int(rand.Int31()) % ensum
for np, _ := range nextother {
rn = rn - np.en
if rn <= 0 {
np.black = true
SetBlack(np.x, np.y)
p.walked = true
return
}
}
}
}
}()
}
}
}
qq 29185807 月牙寂
2015年4月1日