求算两个字符串之间的编辑距离
简述:
设A和B是两个字符串,要用最少的字符操作将字符串A转换为字符串B
字符串操作包括,
1)删除一个字符
2)插入一个字符
3)将一个字符改为另一个字符
算法:
模拟构造一个(m + 1)行,(n+1)列的表格
每一次都是在前一次的计算结果下,得到当前的值
首先是三个特殊情况 用srcStr表示源字符串,dstStr 表示目标字符串
1) 两个空字符串的编辑距离D(srcStr, dstStr) = 0
2) 如果srcStr为空,dstStr不为空,则D(srcStr, dstStr) = dstStr.length(), 即在原空字符串上添加字符,形成dstStr
3) 如果dstStr为空,srcStr不为空,则D(srcStr, dstStr) = srcStr.length(), 及在源字符串上删除其所有字符,直至为空
例子:
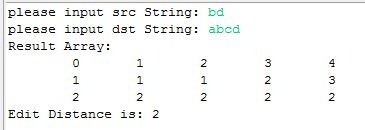
下面实际解决一下从srcStr = "bd" 到 dstStr = "abcd"的过程,
上面这三种情况分别是初始化的时候要做的
首先用一维数组表示两位数组
纵向 i = 0 -> m+1 , d[i * (n + 1)] = i
横向 i = 0 -> n+1, d[i] = i
即:如下图是初始化之后的表格信息,纵向是b,d 横向是a,b,c,d
步骤:
for(i = 1 -> 2) // 2为“bd"的长度
for( j = 1 -> 4 ) // 4 为”abcd"的长度
为了确定d[ i ][ j ]的大小, 需要比较
a) 从d[ i - 1 ][j - 1] 修改字符srcStr[i - 1], 使之变为dstStr[j - 1], 如果srcStr[i - 1] == dstStr[j - 1] 则这一步可以免去
b) 从d[ i - 1 ][ j ] 在srcStr的[ i - 1]处添加一个字符,使字符srcStr[ i - 1 ]变为dstStr[ j - 1 ]
c) 从d[ i ][ j - 1 ] 在dstStr的[ j - 1 ]处删除一个字符, 使字符dstStr[ j - 1 ]变为srcStr[ i - 1]
三者之间的最小值赋给d[ i ][ j ]
代码:
- package dynamic_programming;
- import java.io.BufferedReader;
- import java.io.IOException;
- import java.io.InputStream;
- import java.io.InputStreamReader;
- public class StringToString {
- public static void main(String[] args) {
- System.out.print("please input src String: ");
- InputStream inputStream = System.in;
- InputStreamReader inputStreamReader = new InputStreamReader(inputStream);
- BufferedReader bufferReader = new BufferedReader(inputStreamReader);
- //Get source string
- String srcStr = null;
- try{
- srcStr = bufferReader.readLine();
- }catch(IOException e){
- e.printStackTrace();
- }
- //Get destination string
- String dstStr = null;
- System.out.print("please input dst String: ");
- try{
- dstStr = bufferReader.readLine();
- }catch(IOException e){
- e.printStackTrace();
- }
- //Display the result
- System.out.println("Edit Distance is: "
- + getEditDistance(srcStr, dstStr));
- try{
- bufferReader.close();
- inputStreamReader.close();
- inputStream.close();
- }catch(IOException e){
- e.printStackTrace();
- }
- }
- public static int getEditDistance(String srcStr, String dstStr){
- int m = srcStr.length();
- int n = dstStr.length();
- //use one dimension array to represent two dimension
- //Initializing...
- int d[] = new int[(m + 1) * (n + 1)];
- for(int i = 0;i <= m;i++)
- d[i * (n + 1)] = i;
- for(int i = 0;i <= n;i++)
- d[i] = i;
- //Dynamic Programming...
- for(int i = 1; i <= m;i++){
- for(int j = 1; j <= n;j++){
- int modifyDis = d[(i - 1) * (n + 1) + (j - 1)]
- + (srcStr.charAt(i - 1) == dstStr.charAt(j - 1) ? 0 : 1);
- int addDis = d[(i - 1) * (n + 1) + j] + 1;
- int deleteDis = d[i * (n + 1) + (j - 1)] + 1;
- d[i * (n + 1) + j] = Min(modifyDis, addDis, deleteDis);
- }
- }
- //Display Result
- System.out.println("Result Array: ");
- for(int i = 0; i <= m;i++){
- for(int j = 0; j <= n;j++){
- System.out.print("\t" + d[i * (n + 1) + j]);
- }
- System.out.println();
- }
- return d[m * (n + 1) + n];
- }
- public static int Min(int a, int b, int c){
- int result = a > b ? b : a;
- return result > c ? c : result;
- }
- }
输出测试: