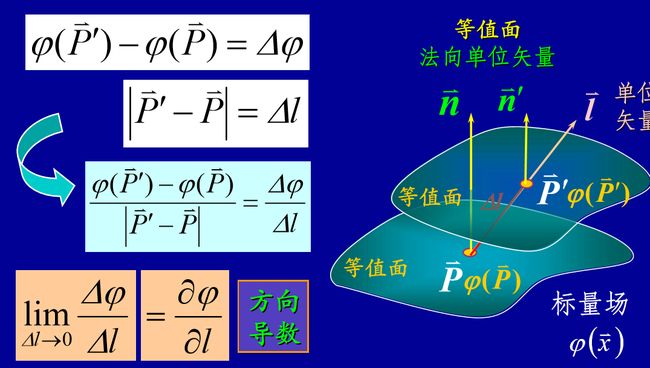
矢量场

立体角

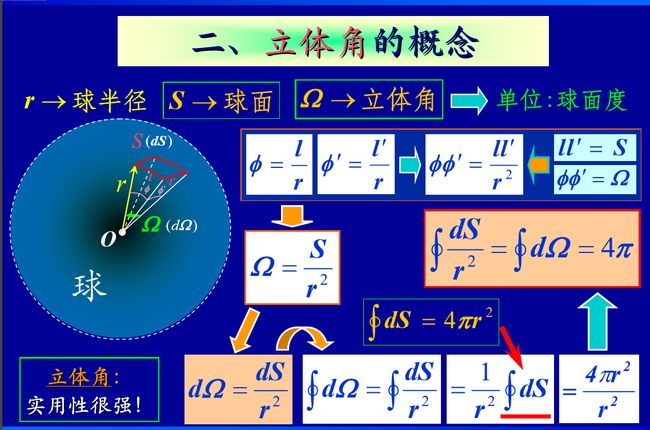
球面度 （steradian，符号∶sr）是 立体角 的 国际单位 。它可算是三维的 弧度 。其英文字是希腊语「立体」（stereos）和弧度（radian）的混合。

例如一个球的球面度是4π，一个椭球的球面度是4π。
其英文表示为 Solid Angle.

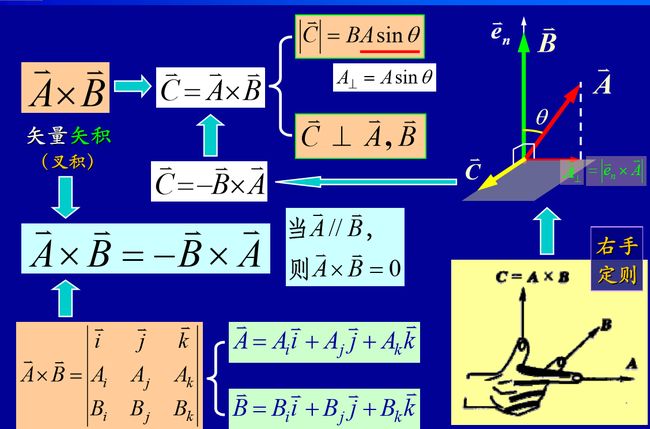
矢量积

A⃗ ×B⃗ =−B⃗ ×A⃗ 

A⃗ ⋅(B⃗ ×C⃗ ) = B⃗ ⋅(C⃗ ×A⃗ ) = C⃗ ⋅(A⃗ ×B⃗ )

=−A⃗ ⋅(C⃗ ×B⃗ ) 等同理——平行六面体体积

A⃗ ×(B⃗ ×C⃗ )=(A⃗ ⋅C⃗ )B⃗ −(A⃗ ⋅B⃗ )C⃗ 

列维-奇维塔符号(Levi-Civita symbol)在张量分析很常用。
它以20世纪初数学家列维-奇维塔命名。
三维
若 (i, j, k) = {1,2,3}, {2,3,1} 或 {3,1,2} （偶置换）
若 (i, j, k) = {3,2,1}, {2,1,3} 或 {1,3,2} （奇置换）
若 i=j, j=k或i=k
例子
3 × 3矩阵的行列式： det(A)=∑3i,j,k=1εijka1ia2ja3k
两支向量的叉积
a×b=c, ci=∑3j,k=1εijkajbk.

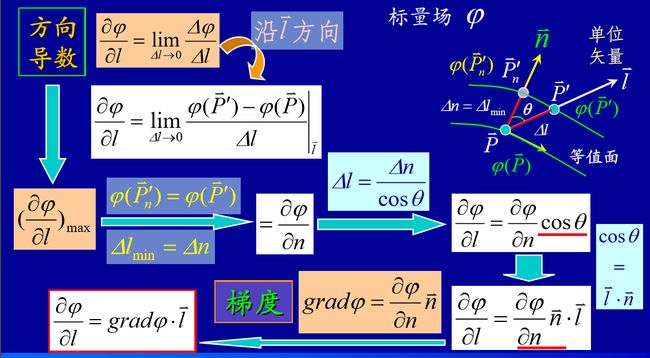
∇u 称为标量场的梯度——微分运算符号，也称矢量微分算子

矢量场的通量和散度

通量
Φ=∮SA⃗ (r)⋅dS⃗ (r)=∮SA(r)cosθdS(r)

散度
limΔτ→0∮SA⃗ (r)⋅dSΔτ 记作 divA

可以证明，在极限存在的情况下，两种定义是等价的。因此也常直接用 ∇F 代表 F 的散度。
由散度的定义可知， divF 表示在某点处的单位体积内散发出来的矢量 F 的通量，所以 divF 描述了通量源的密度。举例来说，假设将太空中各个点的热辐射强度向量看做一个向量场，那么某个热辐射源（比如太阳）周边的热辐射强度向量都指向外，说明太阳是不断产生新的热辐射的源头，其散度大于零。
从定义中还可以看出，散度是向量场的一种强度性质，就如同密度、浓度、温度一样，它对应的广延性质是一个封闭区域表面的通量。

拉普拉斯运算 ∇⋅∇Φ=∇2Φ
拉普拉斯算子 ∇2

环量与旋度

环量
∮CA⃗ ⋅dl⃗ =∮CAcosθdl

旋度
rotA→=n⃗ limΔS→0[∮CA⃗ ⋅dl⃗ ]maxΔS
rotA的大小是矢量场A在给定环量面密度的最大值，rotA的方向就是该点处环量面密度取得最大值的方向。
rotA描述了矢量A在空间某点处漩涡源的强度

斯托克斯定理

∮S∇×A→⋅dS⃗ =∮CA⃗ dl⃗ 

无旋场和无散场
rot(gradu)=∇×∇u=0
div(rotA→)=∇⋅∇×A⃗ =0
无旋场—旋度处处为0
无散场—散度处处为0

亥姆霍兹定理

若矢量场 F(r) 在无限空间处处单值，且其导数连续有界，形成矢量场的源分布在有限空间区域中，则矢量场 F(r) 由其散度和旋度唯一确定，并且可以表示为
F(r)=−∇Φ(r⃗ )+∇×A(r)→