散列

散列（hashing）是一种用于以常数平均时间执行插入、删除和查找的技术，但需要元素间任何排序信息的操作将不会得到有效的支持

理想的散列表数据结构只是一个包含关键字的具有固定大小的数组；每个关键字被映射到从0～TableSize-1这个范围中的某个数，并且被放到适当的单元中。这个映射叫做散列函数（hash function），理想情况下它应该运算简单并且保证任何两个不同的关键字映射到不同的单元。当两个关键字散列到同一个值的情况称为冲突（collision）

解决冲突最简单的两种方法：分离链接法，开放定址法

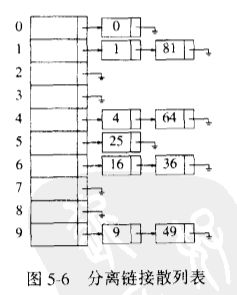
分离链接法（separate chaining）：将散列到同一个值的所有元素保留到一个表中

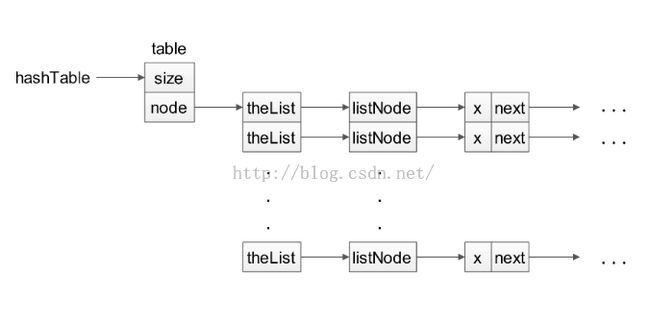
数据结构：

如果散列不包括删除操作，那么最好不要使用表头，因为使用表头不仅不能简化问题，而且还会浪费大量的空间

装填因子（load factor）λ为散列表中的元素个数和散列表大小的比值。执行一次查找所需的工作是计算散列函数值所需要的常数时间加上遍历表所用的时间。表的大小实际上并不重要，装填因子才是重要的。分离散列的一般法则是使表的大小尽量与预料的元素个数差不多（λ≈1）

开放定址法（open addressing hashing）：分离链接散列算法的缺点是需要指针，由于给新单元分配地址需要时间，因此这就导致算法的速度会有减慢。在开放定址散列算法系统中，如果冲突发生，那么就要尝试选择另外的单元，直到找到空的单元为止。一般地，单元h0(X)，h1(X)，h2(X)等相继被试选，其中hi(X) = (Hash(X) + F(i) ) mod TableSize，且F(0) = 0。函数F是冲突解决方法。因为所有的数据都要置入表内，所以开放定址散列法所需要的表比分离散列的大，一般来说对开放定址散列算法来说，装填因子λ应该小于0.5

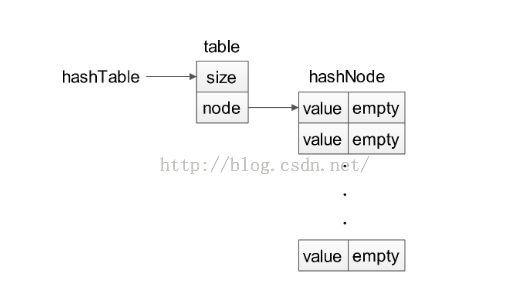
数据结构：

1. 线性探测法：函数F是i的线性函数。这种方法花费的时间相对较多，而且即使表相对较空，占据的单元也会开始形成一些区块，称为一次聚集（primary clustering）

2. 平方探测法：是消除线性探测中一次聚集问题的解决方法，冲突函数为二次函数。对于线性探测，元素几乎填满散列表时表的性能会降低，而对平方探测情况会更糟：一旦表被填充超过一半，当表的大小不是质数时甚至在表被填充一半之前就不能保证一次找到一个空单元了，哪怕表有比一半多一个的位置被填满，那么插入都有可能失败（但概率极低）

【定理】对于平方探测，当表的大小是质数时，如果表至少有一半是空的，则总能插入一个新的元素

虽然平方探测排除了一次聚集，但散列到同一位置上的那些元素将探测相同的备选单元，这叫做二次聚集

3. 双散列（double hashing）：能够排除二次聚集，但要花费额外的乘除计算。对于双散列，一种流行的选择是F(i) = i * hash2(X)：将第二个散列函数应用到X并在距离hash2(X)，2*hash2(X)等处探测，即hi(X) = (hash(X) + i * hash2(X))。若hash2(X)选择的不好结果将是灾难性的。另外，保证所有的单元都能被探测到也很重要。如果表的大小不是质数，那么备选单元可能提前用完，所以使用双散列时应保证表的大小为质数

再散列（rehashing）

对于使用平方探测的开放定址散列法，如果表的元素填的太满，那么操作的运行时间将会变得过长，且insert操作可能失败。解决方法是建立另外一个大约两倍大（后的第一个质数）的表（而且使用一个相关的新散列函数），扫描整个原始散列表，计算每个元素新散列值并将其插入到新表中，这个过程就叫再散列。这是一个十分昂贵的操作，其运行时间为O(N)

再散列可以用平方探测以多种方法实现。一种做法是只要表填满一半就再散列；另一种极端的方法是只有当插入失败时才再散列；第三种方法是途中（middle-of-the-road）策略：当表的装填因子达到一定值时再散列。由于随着装填因子的增加表的性能会下降，因此，以好的截至手段实现的第三种策略可能是最好的选择

二叉树和散列

1. 二叉树也可以用来实现insert和find操作，虽然平均时间界为O(log N)，但二叉树能够支持有序例程。使用散列表不可能找出最小元素，除非准确知道一个字符，否则也不可能有效地查找它。二叉树可以迅速查找到一定范围内的所有项，这是散列表做不到的

2. 散列的最坏情况一半来自实现的缺憾，而有序的输入却可能使二叉树运行得很差，并且平衡查找树实现的代价很高，因此，如果不需要有序的信息，或者输入可能已被排序，那么就应该选择散列