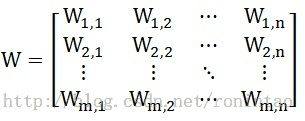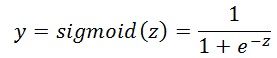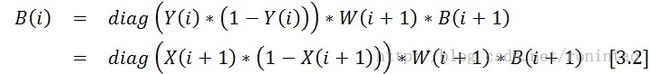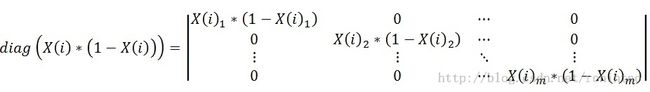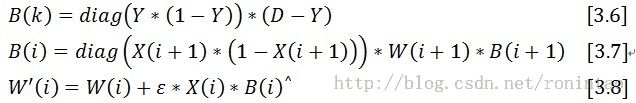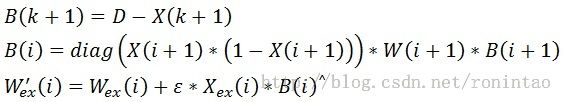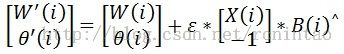【cocos2D-x学习】17.手势识别

【目标】：在cocos2dx中，识别如左滑、上滑之类的简单手势

【参考】：

《动态规划时间规整简介入门》：http://blog.csdn.net/detective_xin/article/details/7986834

《Mouse gestures recognition》：http://www.codeproject.com/Articles/1591/Mouse-gestures-recognition

《现代优化计算方法》：这个是我硕士时期学的一个课本，清华大学出版，才发现还挺有用。。。

一、期望的效果

二、识别的方法

        我现在会的是下面两种：动态时间规整和BP神经网络。另外还有：隐马尔科夫模型HMM，支持向量机SVM。另外，OPENCV中也有手势识别的现成算法，不过我暂时还不会OPENCV。

        就动态时间规整和BP神经网络而言。我个人目前感觉动态时间规整更加适合这个场景（但我参考的Konstantin Boukreev的实现方式用的是BP神经网络），BP神经网络的话对输入维数有严格要求，因此对预处理方法要求更加高。而动态时间规整实现起来也很简单，上面示例的程序就是用DTW来实现的，识别率相当的高。当然神经网络的运用场景更广，掌握了当然没有坏处。

        下面分别介绍两种算法。

三、DTW：动态时间规整

1、Dynamic Time Warping（DTW）要解决的问题

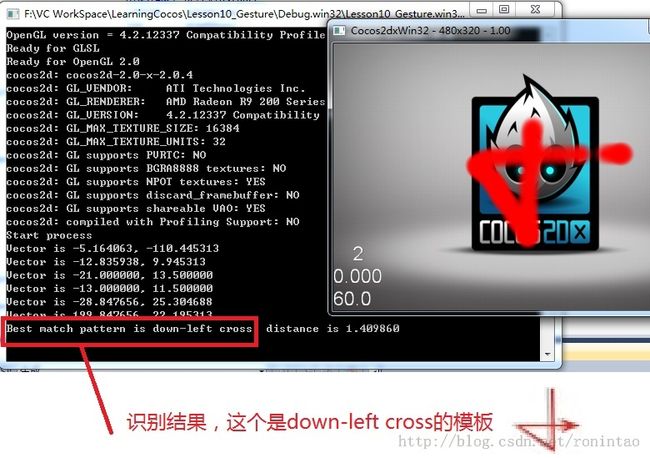
        在识别过程中，最大的麻烦，不是噪声，而是每条边不确定的长度和位置。噪声可以通过平滑的方式，将那些小于一定阈值的边剔除，而轻易排除，但是对于不确定的边长，就很头疼，例如下面的三种图案：

       从肉眼上看，这三个图案是非常相似的。但计算机要看出这一点，则很困难。

       如果仅仅要使得图1和图2相似，还并不复杂，这两者之间实际上只有边长的区别，我们可以使用角度作为值，来进行比较，这样取值后，

       图一：Data_1 = [    0.0f, 90.0f];

       图二：Data_2 = [    0.0f, 90.0f];

       图三：Data_3 = [-10.0f, 10.0f, 90.0f]

       但是这个时候计算欧式距离

       Distance( A, B ) = ( Data_A [0] - Data_B [0] ) ^ 2 + ( Data_A [1] - Data_B [1] ) ^ 2 + ...... +  ( Data_A [n] - Data_B [n] ) ^ 2 

       会发现图3与图1和图2之间差距巨大，这显然与事实并不相符。

       为了解决这个问题，DTW就应运而生了。

2、DTW的基本思路

        欧式距离差距大的原因是因为 10 必须和 90 对应，如果 10 和 0 对应，90和90对应，那么距离不就缩小了吗？引用《动态规划时间规整简介入门》里面的话来说，DTW的基本思路，就是一种时间扭曲，感觉就像是音乐中的多拍音符，使得原来的0占两个身位，对应-10和10，从而缩小了他们之间的距离：

Data_2：  __0__     90

Data_3： -10   10    90

3、DTW的基本方法

         那么，如果找到这样一种对应关系呢？这基于以下的递归：

         对于两个数组 ABCDE 和 UVWX，他们之间的最佳对应关系，应该来源于以下三种方式之一：

         1）E 与 X 对应，D 与 W 对应。这意味着，E 和 X都不需要扭曲，那么 Distance( ABCDE, UVWX ) = Distance( ABCD, UVW ) + Distance( E, X )

         2）E 与 X 对应，D 与 X 对应。那么，E不需要扭曲，X需要扭曲，那么 Distance( ABCED, UVWX ) = Distance(ABCD, UVWX) + Distance( E, X )

         3）E 与 X 对应，E 与 W对应。那么，X不需要扭曲，E需要扭曲，那么 Distance( ABCED, UVWX ) = Distance(ABCDE, UVW) + Distance( E, X )

         其实还有两种情况：E 与 X 不对应，以及 E 与 X 都需要扭曲，不过很容易看出，都是不可能的。

        所以，数组 ABCDE 和 UVWX 之间最佳对应关系的距离，应该是以上三种方式的最小者。

        明眼人很可能会发现，这不明显就是动态规划嘛！没错，不然名字也不会那么接近了。

4、代码

        这里的 mData 是经过平滑等预处理的触屏输入，记录的是鼠标滑动形成的边的角度，是normalized后的方向向量。

float GestureProcessor::getDTWDistance(const VecList & pattern, const int maxStride) {
    //几个辅助宏
#define GET_INDEX(_n, _m)    ( (_m) * MAX_N + (_n) )
#define GET_ELEMENT(_n, _m)  ( output[GET_INDEX(_n, _m)] )
#define GET_DISTANT(_p, _d)  ( ccpDistance(_p, _d) )

    //术语解释：N是data的数据index，M是pattern的数据index
    int MAX_N = mData.size();
    int MAX_M = pattern.size();
    float * output = new float[MAX_N * MAX_M];
    memset(output, 0, sizeof(float) * MAX_M * MAX_N);

    int n = 0;
    int m = 0;
    for ( VecItorC nItor = mData.begin(); nItor != mData.end(); nItor ++, n ++, m = 0 ) {
        for ( VecItorC mItor = pattern.begin(); mItor != pattern.end(); mItor ++, m ++ ) {
            //在 O[n-1][m], O[n][m-1], O[n-1][m-1] 中选最小值
            float minValue;
            if ( n == 0 && m == 0 )
                minValue = 0;
            else if ( n == 0 )
                minValue = GET_ELEMENT(n, m-1);
            else if ( m == 0 )
                minValue = GET_ELEMENT(n-1, m);
            else
                minValue = MIIN( MIIN(GET_ELEMENT(n-1, m), GET_ELEMENT(n, m-1)), GET_ELEMENT(n-1, m-1) );

            GET_ELEMENT(n, m) = GET_DISTANT(*nItor, *mItor) + minValue;
        }
    }

    float ans = GET_ELEMENT( MAX_N - 1, MAX_M - 1 );

    delete [] output;
    return ans;
}

四、BP神经网络

        以下省去了偏微分的推导，主要是因为贴公式太麻烦，本身并不复杂，对证明有兴趣的同学请参阅《现代优化计算方法》，我这里只介绍主体部分，在原书基础上对几个重要公式有部分化简和归并。

1、总体思路

       BP神经网络的总体思路，就是设定一个权值矩阵，给定样本的输入，通过矩阵计算输出，然后将这个输出与期望的输出对比，将误差分解到矩阵各个分量进行调整。

2、如何正向取值

       2.1   先研究单层神经网络：

      （1）记输入为 X，输出为 Y。X 、Y 均为矩阵形式，X 有 n 个分量，是一个 n * 1 的矩阵；Y 有 m 个分量，是一个 m * 1 的矩阵

      （2）将输入 X 输入网络。这个网络上有 m 个神经元，接受来自于 n 条神经的刺激。记总刺激为 Z：

        

         【由于博客里面不好写上标，所以用 W^ 表示 W 的转置矩阵，为统一，后面公式中也这样写。】

          非常需要注意的一点，是这里的公式中用的是转置矩阵，公式来自于《现代优化计算方法》，我也不知道为什么要这样绕。

       （3）式 2-1 中的 W 被称为权矩阵。W 是一个 m * n 的矩阵，W^ 就是一个 n * m 的矩阵：

        

       （4）式 2-1 中的 θ 称为阈值。是一个 m * 1 的矩阵

       （5）得到 Z 之后，根据激活函数，确定 Y 的值

         

       2.2  再研究多层神经网络

       （1）对多层神经网络，包含隐层 Layer(1) 、 Layer(2) 、 …… 、 Layer(k)

                 输入层记为第0层 Layer(0)，这个第0层实际并不存在，也没有任何神经元节点。

                 则 X 是整个网络的输入，我们可以把他当做是第0层的输出。整个网络的输出 Y 是 Layer(k) 的输出。记 L_i 的权矩阵为 W(i)，则 W(i) 的输入 X(i) 是 Layer(i-1) 的输出，由其产生刺激矩阵，进而产生的输出 Y(i) 再作为下一层的输入，继续传递：

            

                【其中，i = 1, 2, 3... k，表示层数】

        （2）将式 2-4 带入 2-3，有

           
               即，第 i 层的输入是 X(i)，输出是 X(i+1)，整个网络的输入是 X(1)，输出是 X(k+1)

        （4）若 X(i) 是 m(i) 维的，则 W(i) 是 m(i) * m(i+1) 维的矩阵。

3、如何反向学习

        3.1  先讨论 θ(i) = 0 的情况，对不为0的情况可以通过后面的讨论归结到本情况

        激活函数设置为

        

       （1）偏差值 B

             上面说到第 i 层的输出是 X(i+1)，这个是根据神经网络的权矩阵算出来的，会与期望值有一定偏差。记其期望值为 D(i+1)，记偏差为

             
             可以看到 B(i) 是一个 m(i+1) * 1 的矩阵。（反复强调行列数的原因，是因为这个在程序里面想起来很麻烦。。。）

       （2）根据 B(i+1) 计算 B(i)

             显然，我们只对最终的输出值 Y，可以获得一个期望值，对于中间隐层的计算中间值，是没有什么期望值的。所以这里的偏差值不能通过式3-1计算，需要通过反向推算，这就是所谓的Back Propagation。

             这里要省略一坨偏微分计算，直接给出最后的计算结果。还是那句话，有兴趣的同学可以参阅《现代优化计算方法》。

            

              其中 diag 是对角矩阵：

              

            【这里和上面的矩阵，都假设数组从 1 开始计数】

       （3）式3-2 有几点需要注意：

              1）B(i) 可以由 i+1 层的数据完全确定

              2）这里有个问题，对于 k 层神经网络，最后一层有：

                B(k) = diag( X(k+1) * (1 - X(k+1)) ) * W(k+1) * B(k+1)

                X(k+1) 和 B(k+1) 都没问题，但是并没有 W(k+1)，所以直接令 W(k+1) 为单位矩阵 I

             3）注意比较 [式 3-2] 和 [式 2-5]，这里的 W 矩阵是没有转置的

       （4）根据 B(i) 调整 W(i)

             1）计算梯度矩阵

                   
                   X(i) 是一个 m(i) * 1 矩阵，B(i) 是一个 m(i+1) * 1 的矩阵，则根据上面的式子（注意转置），可以知道 ▽W(i) 是一个 m(i) * m(i+1) 的矩阵，恰好与 W(i) 相同

             2）学习

                  

                  【其中 ε 是一个新出现的参数，被称为学习效率，设置的越大，收缩的速度越快，但是也可能会导致不收敛】

            3）结合上面两个式子，就可以得到：

                 
            4）最后一个问题：

                注意到 [式 3-2] 需要用到 W 矩阵，那么那里面用的是学习前的 W，还是调整后的 W' 呢？答案是：使用的是学习前的 W

      （5）总结一下：

                

        3.2  如何将 θ 融入 W 矩阵

                总体的思路，类似于OPENGL中的齐次矩阵

       （1）对第 i 层，将输入X(i)增加一维 -1 ，也就是要将 θ 前面的 -1 转换为输入： Xex(i) = (X(i)^, -1)^，即：

                   
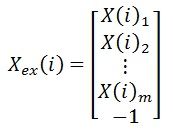
                 权矩阵变形为 Wex(i) = (W(i)^, θ(i))^，即：

               

     （2）对正向计算的影响：

                

                和原来的计算基本没有区别。

    （3）对反向BP的影响：

               

             也就是说，前两个式子不需要变化，只要改变最后的梯度计算和学习即可。

    （4）对上面最后一个式子可以进行分解：

            

            因此，可以得到

           

      3.3  代码

            这里给出了BP神经网络的一个简单实现：http://download.csdn.net/detail/ronintao/6754951