(五)高级数据结构
第十八章 B树
其用于磁盘或其他直接存取辅助存储设备而设计的一种平衡查找树,类似于红黑树,但是降低磁盘I/O操作次数方面要更好一点。
与红黑树不同的是:B树节点可以有许多子女;与红黑树相似之处:每棵含n个节点的B树的高度为O(lgn),但其高度应该会比红黑树小很多
辅存上的数据结构
这次对运行时间的两个主要组成部分分别加以考虑:一,磁盘存取的次数;二,cpu(计算)时间。
B树的定义
假设当关键字从一个节点移动到另外一个节点,无论是与关键字相联系的附属数据,还是指向这样的数据的指针,都随着关键字一起移动。
一棵B树T是具有如下性质的有根数(根为root[T]):
1)每个节点x有以下域:a)n[x],当前存储在节点x中的关键字数
b)n[x]个关键字本身,以非降序存放,因此
c)leaf[x],是一个布尔值,如果x是叶子的话,则他为TRUE,如果x为一个内节点,则为FALSE
2)每个内节点x还包含n[x]+1个指向其子女的指针c1[x],c2[x].....c(n[x]+1)[x].叶节点没有子女
3)各关键字keyi[x]对储存在各子树的关键字范围加以分隔:如果ki为存储在以ci[x]为根的子树中的关键字,则
4)每个叶节点具有相同的深度,即树的高度h
5)每个节点能包含的关键字数有一个上界和下界,这些界可用一个称作B树的最小度数的固定证书t小于等于2来表示
B树的高度
利用不等式:可证
对B树的操作
搜索B树
B-tree-search(x,k)
{
i = 1
while i <= n[x] and k > key(i)[x]
do i = i+1
if i <= n[x] and k = key(i)[x]
then return (x,i)
if leaf[x]
then return NIL
else
Disk-read(c(i)[x])
return B-tree-search(c(i)[x],k)
}
创建一棵空的B树
B-tree-create(T)
{
x = allocate-node()
leaf[x] = TRUE
n[x] = 0
Disk-write(x)
root[T] =x
}
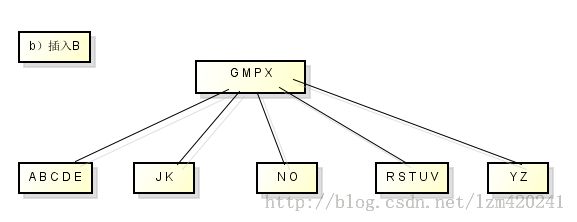
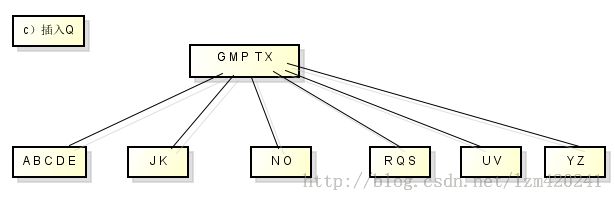
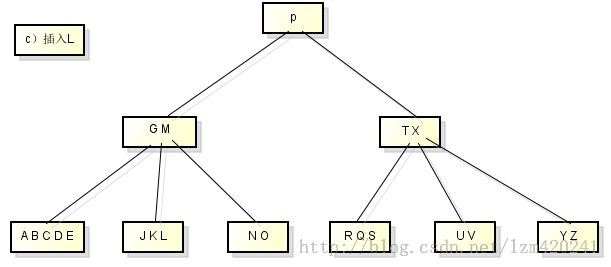
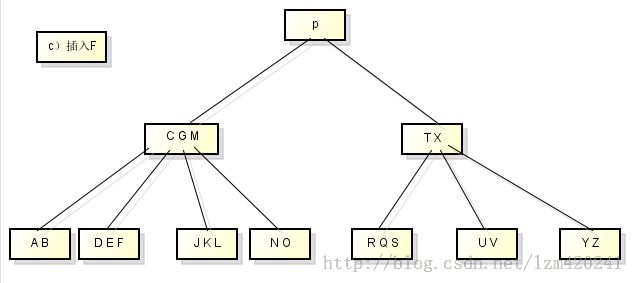
向B树插入关键字
思想:将新关键字插入到一个已存在的叶节点上,因为不能把关键字插入到一个满的叶节点上,故引入一个操作,将一个满的节点y(有2t-1个关键字)按其中间关键字key(t)[y]分裂成两个各含t-1个关键字的节点。中间关键字被提升到y的双 亲节点,以标识两棵新的树的划分点。但是如果y的双亲也是满的,则他必须在新的关键字可以插入前被分裂,满节点分裂动作会沿着树向上传播的。
B树中节点的分裂:
B-tree-split-child(x,i,y)
{
z = allocate-node()
leaf[z] = leaf[y]
n[z] = t-1
for j =1 to t-1
do key(j)[z] = key(y+t)[y]
if not leaf[y]
then for j =1 to t
do c(j)[z] = c(j+t)[y]
n[y] = t-1
for j = n[x]+1 downto i+1
do c(j+1)[x] = c(j)[x]
c(j+1)[x] = z
for j = n[x] downto i
do key(j+1)[x] = key(j)[x]
key(i)[x] = key(t)[y]
n[x] = n[x]+1
disk-write(y)
disk-write(z)
disk-write(x)
}
对B树用单程下行遍历树方式插入关键字
B-tree-insert(T,k)
{
r = root[T]
if n[r] = 2t-1
then s = allocate-node()
root[T] = s
leaf[s] =FALSE
n[s] =0
c(1)[s] = r
B-tree-split-child(s,1,r)
B-tree-insert-nonfull(s,k)
else
B-tree-insert-nonfull(r,k)
}
//把关键字k插入节点x,假定在调用过程时x是非满的。
B-tree-insert-nonfull(x,k)
{
i = n[x]
if leaf[x]
then while i >= 1 and k < key(i)[k]
do key(i+1)[x] = key(i)[x]
i = i-1
key(i+1)[x] =k
n[x] =n[x]+1
disk-write(x)
else while i >=1 and k < key(i)[x]
do i = i-1
i =i+1
disk-read(c(i)[x])
if n[c(i)[x]] = 2t-1
then B-tree-split-child(x,i,c(i)[x])
if k > key(i)[x]
then i = i+1
B-tree-insert-nonfull(c(i)[x],k)
}
从B树中删除关键字
需要保证删除一个节点不能太小
需要分三种情况讨论:
1)如果关键字k在节点x中而且x是个叶节点,则从x中删除k
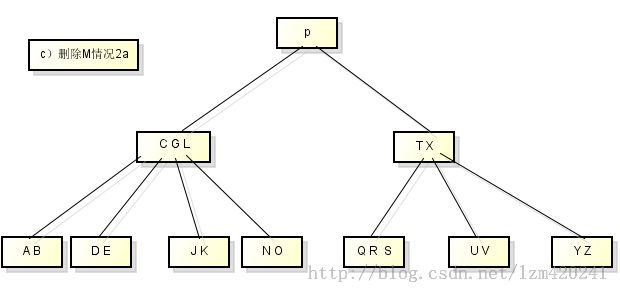
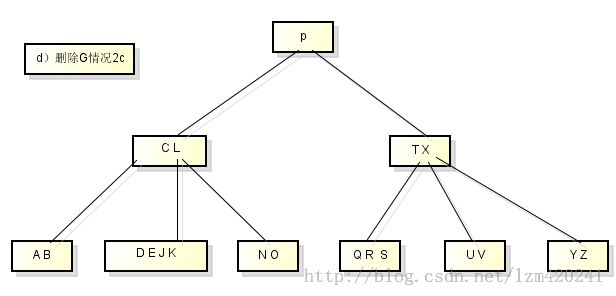
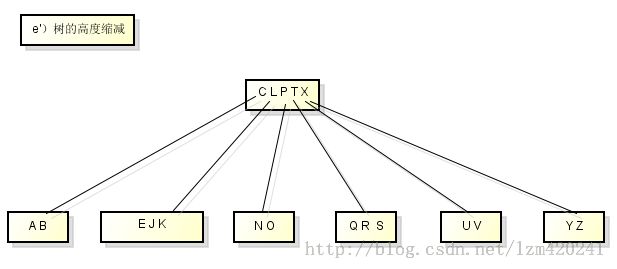
2)如果关键字k在节点x中而且x是个内节点,则需要如下操作:
一棵高为h的B树,他只需O(h)次磁盘存取操作,因为在递归调用该过程之间,仅需O(1)次对disk-read 和disk-write的调用,所需CPU时间为
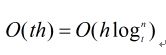 。
。
第十九章 二项堆
可合并堆的数据结构,同时支持一下五中操作:
创建并返回一个不包含任何元素的新堆:Make-heap();
将节点x(其关键字域中已填入了内容)插入堆H中:Insert(H,x)
返回一个指向堆H中包含最小关键字的节点指针:Minmum(H)
将堆H中包含最小关键字的节点删除,并返回一个指向该节点的指针:Extract-min(H)
创建并返回一个包含堆H(1)和H(2)中所有节点的新堆。同时,H(1)和H(2)被这个操作删除Union(H1,H2)
另外还支持以下两种操作:
将新关键字值k(假定它不大于当前的关键字值)赋给堆H中的节点x:Decrease-key(H,x,k)
从堆H中删除节点x:Delete(H,x)
二项树和二项堆
一个二项堆是由一组二项树所构成的。
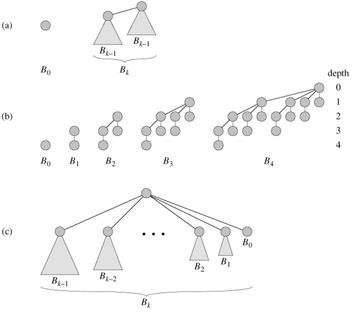
二项树
是一种递归定义的有序树
二项树的性质:
1)共有2^k个节点
2)树的高度为k
3)在深度i处恰有(k,i)个节点,其中i=0,1,2,.....k
4)根的度数为k,它大于任何其他节点的度数,并且,如果根的子女从左到右编号为k-1,k-2,...,0,子女i是子树Bi的根
在一棵包含n个节点的二项树中,任意节点的最大度数为lgn
二项堆
二项堆H满足二项堆性质的二项树组成:
最小堆有序:节点的关键字大于或等于其父节点的关键字
对任意非负数k,在H中至多有一棵二项树的根具有度数k
二项堆的表示
由五个域组成:父节点指针,key,度数,子节点指针,指向x的紧右兄弟的指针sinling[x]
对二项堆的操作
创建一个新的二项堆:Make-binomial-heap()分配并返回一个对象H,且head[H]=NIL
寻找最小关键字
Binomial-heap-minmum(H)
{
y = Nil
x = head[H]
min = ∞
while x != Nil
do if key[x] < min
then min = key[x]
y = x
x = sibling[x]
return y
} 合并两个二项堆
Binomial-link(y,z)//将两个树的根节点连接起来
{
p[y] = x
sibling[y] = child[z]
child[z] = y
degree[z] = degree[z]+1
}
Binomial-heap-union(H1,H2)//反复连接根节点的度数相同的各二项树
{
H = Make-binomial-heap()
head[H] = Binomial-heap-merge(H1,H2)//将H1和H2的根 表合并成一个按度数的单调递增次序排列的链表
free th objects H1 and H2 but not the lists they point to
if head[H] = Nil
then return H
prev[x] = Nil
x = head[H]
next[x] = sibling[x]
while next[x] != Nil
do if (degree[x] != degree[next[x]]) or (sibling[next[x]] != Nil and degree[next[x]]= degree[x])
then prev[x] = x //cases 1 and 2
x = next[x] //cases 1 and 2
else if key[x] <= key[next[x]]
then sibling[x] = sibling[next[x]] //case 3
Binomial-link(next[x],x) //case 3
else if prev[x] = Nil
then head[H] = next[x] //case 4
else
sibling[prev[x]] = next[x] //case 4
Binomial-link(x,next[x]) //case 4
x = next[x] //case 4
next[x] = sibling[x]
return H
} 插入一个节点
Binomial-heap-insert(H,x)
{
H' = Make-binomial-heap()
p[x] = Nil
child[x] = Nil
sibling[x] = Nil
degree[x] = 0
head[H'] = x
H = Binomial-heap-Union(H,H')
}
抽取具有最小关键字的节点
Binomial-heap-extract-min(H)
{
find the root x with the minimum key in the root list of H and remove x from the root list of H
H' = Make-binomial-heap()
reverse the order of the linked list of x's children,setting the p field of each child to Nil,and set head[H']to
point to the the head of resulting list
H = Binomial-heap-union(H,H')
return x
}
减小关键字的值
Binomial-heap-decrease-key(H,x,k)
{
if k > key[x]
then error "new key is geater than current key"
key[x] = k
y = x
z = p[y]
while z != Nil and key[y] < key[z]
do exchange key[y] <-> key[z]
// if y and z hava satellite fields,exchange then too
y = z
z = p[y]
}
删除一个关键字
Binomial-heap-delete(H,x)
{
Binomial-heap-decrease-key(H,x,-∞)
Binomial-heap-extract-min(H)
}
第二十章 斐波那契堆
用于解决诸如最小生成树和寻找单源最短路径等问题
斐波那契堆由一组树构成,相比于二项堆,斐波那契堆更加松散,而以平摊分析为指导思想来斐波那契堆的这种数据结构是很好的例子。
斐波那契堆不能有效的支持search操作。
斐波那契堆的结构
斐波那契堆由一组最小堆有序树构成,但堆中的树不一定是二项树
二项堆中树都是有序的,而斐波那契堆中的树都是有根而无序的
势函数:
(t(H)表示H的根表中树的棵树,m(H)表示H中被标记的节点个数)
最大度数
可合并堆的操作
如果一个有n个节点的斐波那契堆由一组无序二项树构成,则D(n)=O(lgn)
创建一个新的斐波那契堆,过会Make-fib-heap分配并返回一个斐波那契堆对象H,且n[H]=0,min[H]=Nil;此时H中还没有树。故其平摊代价等于O(1)的实际代价
插入一个节点
Fib-heap-insert(H,x)
{
degree[x] = 0
p[x] = Nil
child[x] = Nil
left[x] = x
right[x] = x
mark[x] = FALSE
concatenate the root list containing x with root list H //把 (一系列事件、事情等)联系起来
if min[H] = Nil or key[x] < key[min[H]]
then min[H] = x
n[H] = n[H]+1
}
寻找最小节点
合并两个斐波那契堆
Fib-heap-union(H1,H2)
{
H = Make-fib-heap()
min[H] = min[H1]
concatenate the root list of H2 with the root list of H
if (min[H2] = Nil) or (min[H2]!= Nil and key[min[H2]] < key[min[H1]])
then min[H] = min[H2]
n[H] = n[H1]+n[H2]
free the objects H1 and H2
return H
} 其平摊代价:
抽取最小节点
Fib-heap-extract-min(H)
{
z = min[H]
if z != Nil
then for each child x of z
do add x to the root list of H
p[x] = Nil
remove z from the root list of H
if z = right[z]
then min[H] = Nil
else
min[H] = right[z]
Consolidate(H)
n[H] = n[H]-1
return z
}
/*
Consolidate(H):合并H的根表,即减少斐波那契堆中树的数目
具体:1)在根表中找出两个具有相同的度数的根x和y,且key[x] <= key[y]
2)将y链接到x
*/
Consolidate(H)
{
for i = 0 to D(n[H])
do A[i] = Nil
for each node w in the root list of H
do x = w
d = degree[x]
while A[d]!= Nil
do y = A[d]
if key[x] > key[y]
then exchange x<-> y
Fib-heap-link(H,y,x)
A[d] = Nil
d = d+1
A[d] = x
min[H] = Nil
for i= 0 to D(n[H])
do if A[i] != Nil
then add A[i] to the root list of H
if min[H] = Nil or key[A[i]] < key[min[H]]
then min[H] = A[i]
}
Fib-heap-link(H,y,x)
{
remove y from the root list of H
make y a child of x,incrementing degree[x]
mark[y] = FALSE
}
抽取最小节点的平摊代价:
减少一个关键字与删除一个节点
减少一个关键字:
Fib-heap-decrease-key(H,x,k)
{
if k > key[x]
then error"new key is greater than current key"
key[x] = k
y = p[x]
if y != Nil and key[x] < key[y]
then Cut(H,x,y)
Cascading-cut(H,y)
if key[x] < key[min[H]]
then min[H] = x
}
Cut(H,x,y)
{
remove x from the child of list of y ,decrementing degree[y]
add x to the root list of H
p[x] = Nil
mark[x] = FALSE
}
Cascading-cut(H,y)
{
z = p[y]
if z != Nil
then if mark[y] = FALSE
then mark[y] = TRUE
else
CUT (H,y,z)
cascading-cut(H,z)
}
势的改变至多为:
故其平摊代价为:
Fib-delete(H,x)
{
Fib-heap-decrease-key(H,x,-∞)
Fib-heap-extract-min(H)
} 平摊代价为:
最大度数的界
即证明一个包含n个节点的斐波那契堆中,节点的最大度数D(n)为O(lgn)
第二十一章 用于不相交集合的数据结构
不相交集合有两个重要操作:找出给定的元素所属的集合和合并集合
可通过链表的方式来实现,另外一种更为有效的,采用有根树的表示方法
不相交集合上的操作
不相交集合数据结构保持一组不相交的动态结合S={s1,s2,....,sk},每个集合通过一个代表来识别,代表即集合中某个成员。
设x表示成一个对象,我们希望支持一下操作:
Make-set(x):建立一个新的集合,其唯一成员(因而其代表)就是x。因为各集合是不相交的,故要求x没有在其他集合中出现过
Union(x,y):将包含x和y的动态集合(比如书Sx和Sy)合并为一个新的集合(即这两个集合的并集)。
Find-set(x):返回一个指针,指向包含x的(唯一)集合的代表
不相交集合数据结构的应用
用于确定一个无向图中连通子图的个数
Connected-components(G)
{
for each vertex u ∈ V[G]
do Make-set(u)
for each edge (u,v) ∈ E[G]
do if Find-set(u) != Find-set(v)
then Union(u,v)
}
Same-component(u,v)
{
if Find-set(u) = Find-set(v)
then return TRUE
else
return FALSE
}
不相交集合的链表表示
其平均每个操作需要Θ(n)时间
一种加权合并启发式策略
若我们将一个短的表加入一个长的表上面,那么我们所需时间是O(m+nlgn)
不相交集合森林
改进运行时间的启发式策略
第一种:按秩合并
第二种:路径压缩
按秩合并的伪代码:
Make-set(x)
{
p[x] = x
rank[x] = 0
}
Union(x,y)
{
Link(Find-set(x),Find-set(y))
}
Link(x,y)
{
if rank[x] > rank[y]
then p[y] = x
else
p[x] = y
if rank[x] = rank[y]
then rank[y] = rank[y]+1
} 路径压缩的伪代码:
Find-set(x)
{
if x != p[x]
then p[x] = Find-set(p[x])
return p[x]
}
Find-set有一种两趟方法:一趟沿查找路径上升,直至找到根;第二趟是沿路径下降,以便更新每个节点,使之直接指向根。
* 带路径压缩的按秩合并的分析