【Qtree】Query on a tree系列LCT解法
Qtree1-7
Qtree1 裸的树链剖分,当然也可以用LCT写,就不说什么了...
Qtree2 倍增lca,当然也可以用LCT写,就不说什么了...
Qtree3 裸的树链剖分,当然也可以用LCT写,就不说什么了...
接下来的Qtree4-7才是重点
推荐顺序(7->6->4->5),因为写了7就可以改一改贴到6,写了4就可以改一改贴到5了,瞬间少写两题
Qtree4 我已经想到了一个很好的LCT写法,只可惜这里空白太小,写不下了
Qtree5更简单一些,推荐先写5,或者写这题的不带边权版bzoj1095
—————————————————————————分割线——————————————————————————————
这题的做法很多,有动态树分治,树分治和其他的算法
我的写法是受到Qtree7的启发,听说Qtree7LCT的做法可以扩展到这题,于是就写了一发
这题用到的是Qtree7的两个思想之一,就是用一个数据结构维护虚边连接的子树的信息。
这题是用set维护。
首先把边权附到儿子结点上,记为len(len会引发很多细节问题,一定要小心)
实边上的信息就维护一个lmax,rmax,maxs,sum,类似线段树维护最长连续0/1串的长度
虚边就类似点分治时的想法,记录只到x点的链,和x子树中已经构成路径的两个白点(只管虚子树)
但是定义有一些区别
lmax这个子splay表示的一段重链最浅的白点出发的最长链长,rmax从该实链最深的白点出发的最长链长,maxs即答案,包括实边虚边的最远两白点距离 ,sum表示该子splay段实链总长
为了叙述方便,其他的一些定义:ls左儿子,rs有儿子
先讨论虚子树对maxs的影响,实边要复杂一些
最长和次长到x的链可以合并成一条路径
子树里已经形成的最大路径也可以更新
如果x是白点,那么最长链就可以更新了
虚子树信息的维护主要是在access中的虚实切换
对于要从实变虚的原右儿子,maxs[rs]扔进路径的set里,lmax[rs]扔进链的set里,因为要到x点,所以是lmax
同样,从虚变实的新右儿子,把maxs[y]从set里删去,把lmax[y]从set里删去
虚部就完成了
对于实链我们可以发现一个性质,LCT中splay的任意一个子树,对应的都是原树中实链连续的一段
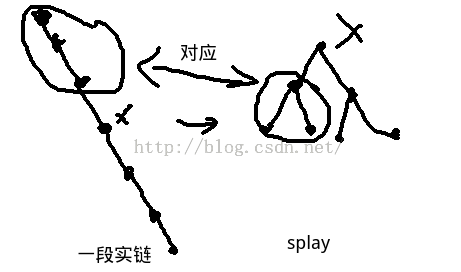
我们在线段树的update合并左右区间时不可能向左向右暴力找到最远的1,更新答案
同样,我们也不能在splay里找到原树中紧邻x上面的点,把它splay上来更新答案
但一个合法的路径要穿过x点,就要过紧邻x上面的点,和紧邻x下面的点
所以我们要记lmax,rmax
然后就是写到吐血激动人心的update了
先更新lmax和rmax
lmax要过整棵子splay的最浅点
那么有lmax[x]=max(lmax[ls]//不过x
,max(虚链中最长+整个左儿子代表的一段,lmax[rs]+整个左儿子代表的一段))
rmax同理,注意x对应的这条边,会有一些细节问题
于是maxs就又有了两种新的更新方式
maxs[x]=max(maxs[x],rmax[rs]+max(虚链,lmax[rs]))
maxs[x]=max(maxs[x],lmax[rs]+max(虚链,rmax[ls]))
然后更新方式就完了
然后就没有然后了
O(nlog^2)卡常警报
不过当set的size比较大时,说明虚边很多,树的深度不深,LCT的操作次数要少一些
如果树的深度深,那么set的size又比较小,所以两个log并不严格
#include<bits/stdc++>
const int maxn=200010,maxm=200010,inf=1e9;
using namespace std;
int n,Q,pre[maxm],now[maxn],son[maxm],val[maxm],tot,ans=-inf,col[maxn];char op[5];//0白1黑
void add(int a,int b,int c){pre[++tot]=now[a],now[a]=tot,son[tot]=b,val[tot]=c;}
inline int fir(multiset<int> &s){return s.size()?*s.rbegin():-inf;}//最大,因为c++是左闭右开,所以s.end()不是最后一个,要--s.end()才是
inline int sec(multiset<int> &s){return s.size()>1?*(++s.rbegin()):-inf;}
struct Tlct{
#define ls ch[x][0]
#define rs ch[x][1]
int ch[maxn][2],fa[maxn],lmax[maxn],rmax[maxn],maxs[maxn],sum[maxn],len[maxn],w[maxn];
//lmax这个子splay表示的一段重链最浅的点出发的最长链长,rmax从该实链最深的点出发的最长链长,maxs即答案,最远两白点距离
//len当前点和父亲之间的边长度,sum该段实链总长 w表示颜色 白色为0表示有一个白点,距离可以是0,黑色为-inf,表示无白点
multiset<int> chain[maxn],path[maxn];//chain 链 path 路径 用来存虚边信息
inline int which(int x){return ch[fa[x]][1]==x;}
inline bool isroot(int x){return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;}
void init(){for (int i=0;i<=n;i++) lmax[i]=rmax[i]=maxs[i]=-inf;}
void update(int x){
assert(x);
sum[x]=sum[ls]+sum[rs]+len[x];
int cha=max(w[x],fir(chain[x]));
int L=max(cha,rmax[ls]+len[x]);//从左子树(实链中更浅的点)或虚边的白点来的最远链长
int R=max(cha,lmax[rs]);//同理
lmax[x]=max(lmax[ls],sum[ls]+len[x]+R);//要想清楚加不加len[x]
rmax[x]=max(rmax[rs],sum[rs]+L);
maxs[x]=max(rmax[ls]+len[x]+R,lmax[rs]+L);
maxs[x]=max(maxs[x],max(maxs[ls],maxs[rs]));
maxs[x]=max(maxs[x],fir(path[x]));
maxs[x]=max(maxs[x],fir(chain[x])+sec(chain[x]));
if (w[x]==0) maxs[x]=max(max(maxs[x],fir(chain[x])),0);//如果这是白点,就可以用子树中的链更新
}
void rotate(int x){
assert(x);
int y=fa[x],z=fa[y],nx=which(x),ny=which(y);
fa[ch[x][!nx]]=y,ch[y][nx]=ch[x][!nx];
fa[x]=z;if (!isroot(y)) ch[z][ny]=x;
fa[y]=x,ch[x][!nx]=y;update(y);
}
void splay(int x){
for (;!isroot(x);){
int y=fa[x];
if (isroot(y)) rotate(x);
else if (which(x)==which(y)) rotate(y),rotate(x);
else rotate(x),rotate(x);
}update(x);
}
void access(int x){
for (int y=0;x;y=x,x=fa[x]){
splay(x);
if (rs) path[x].insert(maxs[rs]),chain[x].insert(lmax[rs]);
if (y) path[x].erase(path[x].find(maxs[y])),chain[x].erase(chain[x].find(lmax[y]));
rs=y,update(x);
}
}
void modify(int x){
access(x),splay(x);
col[x]^=1,w[x]=!col[x]?0:-inf;
update(x),ans=maxs[x];
//for (int i=1;i<=3;i++) print(i);
}
void print(int x){printf("x%d fa%d ls%d rs%d lmax%d rmax%d maxs%d sum%d len%d\n",x,fa[x],ls,rs,lmax[x],rmax[x],maxs[x],sum[x],len[x]);}
}T;
void dfs(int x){
for (int y=now[x];y;y=pre[y]) if (son[y]!=T.fa[x]){
T.fa[son[y]]=x,T.len[son[y]]=val[y],dfs(son[y]);
T.chain[x].insert(T.lmax[son[y]]),T.path[x].insert(T.maxs[son[y]]);
}T.update(x);
}
int main(){
scanf("%d",&n),T.init();
for (int i=1,x,y,z;i<n;i++) scanf("%d%d%d",&x,&y,&z),add(x,y,z),add(y,x,z);
dfs(1),ans=T.maxs[1],scanf("%d",&Q);
for (int i=1,x;i<=Q;i++){
scanf("%s",op+1);
if (op[1]=='A'){
if (ans<0) puts("They have disappeared.");
else printf("%d\n",ans);
}
else scanf("%d",&x),T.modify(x);
}
return 0;
}
/*
6
1 2 1
1 3 1
3 4 2
3 5 2
3 6 2
7
A
C 4
C 5
C 6
A
*/
Qtree5
qtree4的弱化版,注意初始都是是黑点,求的是最近
Qtree6
很显然,树链剖分是可捉此题的
开两棵树,一棵白,一棵黑,记siz[x][0/1]表示子树中还有多少与之连通的同色点
再维护dfs序最小的连通的同色点(线段树里就记最左边的1的位置)
修改颜色时,把x到该点的路径上,重链就区间减,轻链就暴力减
——————————————————————————LCT写法————————————————————————————
也是记两棵树,一棵黑一颗白,对于虚边的siz直接用上面的方法,新开一个siz数组维护一下就好了
但是还有一个问题没有解决,如果改色时暴力link-cut,显然菊花图时修改的边数可以达到O(n)级别
于是就有了一个巧妙的写法,当一个点从白变黑时,只在白树里cut掉它和父亲的边,只在黑树里link上它和父亲的边
也就是保证黑白树中的每条边的儿子一定是黑/白色的,父亲则可能是其他颜色
询问时找到最浅的点,白点就在白树里询问,黑点就在黑树里询问,但要注意根要特判
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
const int maxn=100010,maxm=200010;
using namespace std;
int n,Q,pre[maxm],now[maxn],son[maxm],tot,f[maxn],col[maxn];char ch;
void add(int a,int b){pre[++tot]=now[a],now[a]=tot,son[tot]=b;}
void read(int &x){
for (ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
int t;if (ch=='-') t=-1,ch=getchar();else t=1;
for (x=0;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
x=x*t;
}
struct Tlct{
#define ls ch[x][0]
#define rs ch[x][1]
int fa[maxn],ch[maxn][2],siz[maxn],s[maxn];
inline int which(int x){return ch[fa[x]][1]==x;}
inline bool isroot(int x){return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;}
void update(int x){siz[x]=siz[ls]+siz[rs]+s[x]+1;}
void rotate(int x){
int y=fa[x],z=fa[y],nx=which(x),ny=which(y);
fa[ch[x][!nx]]=y,ch[y][nx]=ch[x][!nx];
fa[x]=z;if (!isroot(y)) ch[z][ny]=x;
fa[y]=x,ch[x][!nx]=y;update(y);
}
void splay(int x){
for (;!isroot(x);){
int y=fa[x];
if (isroot(y)) rotate(x);
else if (which(x)==which(y)) rotate(y),rotate(x);
else rotate(x),rotate(x);
}update(x);
}
void access(int x){
for (int y=0;x;y=x,x=fa[x]){
splay(x);
if (rs) s[x]+=siz[rs];
if (y) s[x]-=siz[y];
rs=y,update(x);
}
}
void link(int x){
access(f[x]),splay(f[x]),splay(x);
ch[f[x]][1]=x,fa[x]=f[x],update(f[x]);
}
void cut(int x){access(x),splay(x),fa[ls]=0,ls=0,update(x);}
int getroot(int x){
access(x),splay(x);
while (ls) x=ls;
return x;
}
int query(int x){
int c=col[x];x=getroot(x),splay(x);
return col[x]==c?siz[x]:siz[rs];
}
}T[2];
void dfs(int x){
for (int y=now[x];y;y=pre[y]) if (son[y]!=f[x]){
f[son[y]]=T[col[son[y]]].fa[son[y]]=x;
dfs(son[y]),T[col[son[y]]].s[x]+=T[col[son[y]]].siz[son[y]];
}
T[0].update(x),T[1].update(x);
}
int main(){
scanf("%d",&n);
for (int i=1,x,y;i<n;i++) read(x),read(y),add(x,y),add(y,x);
dfs(1),read(Q);
for (int i=1,op,x;i<=Q;i++){
read(op),read(x);
if (!op) printf("%d\n",T[col[x]].query(x));
else{
if (f[x]) T[col[x]].cut(x),T[col[x]^1].link(x);
col[x]^=1;
}
}
return 0;
}
Qtree7
和Qtree6类似,维护虚边信息用set,因为维护最大值不能像维护siz一样直接加和减,所以要开一个set,细节稍微多一点
#include<set>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
const int maxn=100010,maxm=200010;
using namespace std;
int n,Q,pre[maxm],now[maxn],son[maxm],tot,col[maxn],f[maxn];char ch;
void add(int a,int b){pre[++tot]=now[a],now[a]=tot,son[tot]=b;}
void read(int &x){
for (ch=getchar();!isdigit(ch)&&ch!='-';ch=getchar());
int t;if (ch=='-') t=-1,ch=getchar();else t=1;
for (x=0;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
x=x*t;
}
struct Tlct{
#define ls ch[x][0]
#define rs ch[x][1]
int ch[maxn][2],fa[maxn],maxs[maxn],val[maxn];multiset<int> s[maxn];
inline bool isroot(int x){return (ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x);}
inline bool which(int x){return ch[fa[x]][1]==x;}
inline void update(int x){
maxs[x]=val[x];
if (s[x].size()) maxs[x]=max(maxs[x],*s[x].rbegin());
if (ls) maxs[x]=max(maxs[x],maxs[ls]);
if (rs) maxs[x]=max(maxs[x],maxs[rs]);
}
void rotate(int x){
int y=fa[x],z=fa[y],nx=which(x),ny=which(y);
fa[ch[x][!nx]]=y,ch[y][nx]=ch[x][!nx];
fa[x]=z;if (!isroot(y)) ch[z][ny]=x;
fa[y]=x,ch[x][!nx]=y;update(y);
}
void splay(int x){
for (;!isroot(x);){
int y=fa[x];
if (isroot(y)) rotate(x);
else if (which(x)==which(y)) rotate(y),rotate(x);
else rotate(x),rotate(x);
}
update(x);
}
void access(int x){
for (int y=0;x;y=x,x=fa[x]){
splay(x);
if (rs) s[x].insert(maxs[rs]);
rs=y;
if (y) s[x].erase(s[x].find(maxs[y]));
update(x);
}
}
int getroot(int x){
access(x),splay(x);
while (ls) x=ls;
return x;
}
void link(int x){
access(f[x]),splay(f[x]),splay(x);
ch[f[x]][1]=x,fa[x]=f[x],update(f[x]);
}
void cut(int x){access(x),splay(x),fa[ls]=0,ls=0,update(x);}
void modify(int x,int v){access(x),splay(x),val[x]=v,update(x);}
int query(int x){
int c=col[x];x=getroot(x),splay(x);
return c==col[x]?maxs[x]:maxs[rs];
}
}T[2];
void dfs(int x){
for (int y=now[x];y;y=pre[y]) if (son[y]!=f[x]){
f[son[y]]=T[col[son[y]]].fa[son[y]]=x;
dfs(son[y]),T[col[son[y]]].s[x].insert(T[col[son[y]]].maxs[son[y]]);
}
T[0].update(x),T[1].update(x);
}
int main(){
scanf("%d",&n);
for (int i=1,x,y;i<n;i++) read(x),read(y),add(x,y),add(y,x);
for (int i=1;i<=n;i++) read(col[i]);
for (int i=1;i<=n;i++) read(T[0].val[i]),T[1].val[i]=T[0].val[i];
dfs(1),read(Q);
for (int i=1,op,x,y;i<=Q;i++){
read(op),read(x);
if (op==0) printf("%d\n",T[col[x]].query(x));
if (op==1){
if (f[x]) T[col[x]].cut(x),T[col[x]^1].link(x);
col[x]^=1;
}
if (op==2) read(y),T[0].modify(x,y),T[1].modify(x,y);
}
return 0;
}