neural network and deep learing(笔记一)

第一章：运用NN识别手写数字

人工智能已经在几乎所有需要思考的领域超过了人类,但是在那些人类和其它动物不需要思考就能完成的事情上,还差得很远

                                        ——Donald Knuth

正如上边这句话所言，我们在识别数字时完全是无意识的情况下完成的，但想要将这一动作抽象成计算机程序却是十分困难的。比如对数字9的解析：其上边是个圈，右下方是条曲线，这很难用程序语言进行精确的描述。

​NN处理这一问题的思想是，运用大量的样本（也称为训练集）并从中自动学习到识别数字的规则。

本章主要介绍神经网络的基本单元，结构，学习算法。需要注意的是，虽然本文关注的是手写数字识别，但其思想完全适用于计算机视觉、语音识别、NLP等其他领域。

一、网络基本单元：感知机和sigmoid神经元

感知机：下图就是perceptrons的结构，它包括多个输入和单个二进制输出，当输入组合超过某一阈值时输出1，低于某一阈值时输出为0。

可以将这一模型理解为通过对证据（输入）的权衡（权值）作出最终的决策（输出）。可以看到，权值和阈值的取值影响着最终的输出，权值的大小对应着相应输入的重要程度，而阈值代表着作出决策的意向程度。 为了进一步简化其数学模型，感知机的学习规则可以表示如下：

这里的b就是阈值的相反数，称为偏置。所以激活函数就可以表示为:

Perceptron的问题在于，当我们对权值和偏置进行微调时，其输出的变化太大，这使得我们无法通过微调参数获得我们想要的结果，即参数的微调使得输出的变化也较小。由此就出现了sigmoid神经单元。Sigmoid神经单元的模型和感知机的类似，但sigmoid的激活函数是：

下图是sigmoid函数和感知机激活函数的曲线，可以看到，sigmoid函数比阶跃函数更加的平滑，这种平滑性也就意味着权值和偏置的微调可以使得输出也产生微小的变化。

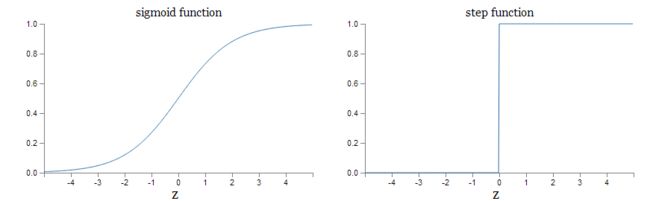
下述公式可以更清楚的看到，输出的变化和参数的变化的成线性关系的，而由于激活函数是指数型，偏微分的计算也更加的简单。

​二、神经网络结构
NN整体包括输入层，隐含层和输出层。输入层由输入数据决定，输出层由类别结果决定，重点是隐含层的设计。同时NN包含两大类别，一是传统的FNN，即前向传播网络，它的特点是上一层的输出作为下一层的输入；一种是RNN，即反馈神经网络，这种网络中存在反馈回路，神经元在激活状态时会持续一段时间，同时它会刺激其他神经元以同样的方式运作。本章则主要讲解FNN。

手写数字识别可以分为两个问题，一个是数字分割，一个是数字识别。分割问题不做赘述。本文用的结构如下：28*28个神经元的输入层，n个神经元的隐含层和10个神经元的输出层。

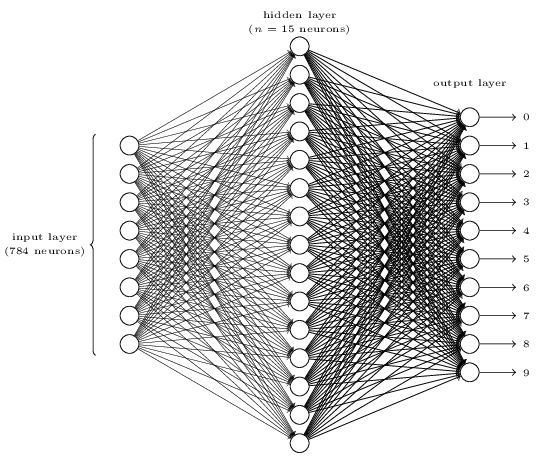
结构确定后，需要确定训练集和学习算法。数字训练集最常用的就是MNIST，它包含70000个数字图像，每个图像大小为28*28，其中训练集60000，测试集10000。同时我们需要选取学习算法来确定网络参数。这里我们选用的是MSE（均方误差函数），即：

有人可能觉得引入一个MSE很是唐突。因为我们的目的是提升数字识别的精确度，那为什么不直接通过调整网络参数来提高精确度呢？原因是数字识别的准确度和网络参数之间并没有很平滑的函数关系，也就没法通过调整参数来较好的实现准确度的提高。反之，利用MSE就可以达到这一效果。当然，目标函数还有很多其他的形式，在后续内容中将做详细介绍。

目标函数最小化的常用算法就是梯度下降算法，下边公式就是GD的数学思想。参数v1和v2的改变促使C发生改变，为了使C减小，对可变参数v就可以使它随着梯度相反的方向改变，这样C就逐渐减小。

将这种思想运用到NN的网络学习中，即：

梯度下降算法也会遇到一些问题，比如之后将要谈到的梯度弥散和膨胀。同时我们有也要注意到目标函数的定义中存在对n个样本求均值误差的计算，这个计算成本是非常高的，所以又提出了SGD。SGD的思想是从训练集中随机抽取一小部分样本来计算梯度，然后再对这个样本求均值梯度，以近似整体梯度。虽然这种近似并非完美，但我们需要的是减小C，这也就意味着对梯度的计算并非一定要精确。其计算公式如下：

相应的参数更新公式：

这里有两个小概念需要注意：一是抽取的样本也被称为小批量（mini-batch），二是对整个训练集穷尽抽样求梯度的过程称为轮（epoch）。

数据集和算法确定后，接下来就是具体实现了。在运用数据集之前，我们一般将前面提到的60000训练集分为50000个训练集合10000的验证集。验证集的提出有助于我们我们对网络超参（诸如隐含层神经元个数，mini-batch大小，学习率，轮数等）的选定。

三、具体代码实现：
首先是整个网络初始化的代码

接下来是sigmoid函数实现代码，并运用了Numpy定义了函数的矢量化形式：

然后是前向传播算法的实现：可以看到，先是z=w*x+b的线性运算，然后是经过非线性激活单元sigmoid输出。

最重要的部分就是梯度计算和参数更新。梯度计算运用的是SGD：

SGD算法先对训练集进行shuffling，接着进行抽样，针对每个mini-batch计算其梯度并更新参数。
由下图可知，超参的选择至关重要。这需要一些trick。在后续章节会就这一问题做详细讲解。

除了NN用作数字识别外，通过对SVM中的参数的优化也可以达到98.5%的准确率。现今在MNIST上的state-of-art是99.79%。

虽然NN的性能很好，但这之中权值和偏置的自动学习对于我们而言仍是一个谜团，我们并不知道这些参数的自动学习意味着什么。拿人脸识别为例，我们会对这一问题进行分解：图像是否在左右上方有眼睛？在中间是否有鼻子？……然后我们对这些问题做进一步分解，一直这样进行下去，直到最终的子问题可以在单个像素的层次上得到答案，这样再通过多层建立抽象更高层次的概念，从而回答原始问题。DNN相对于浅层网络存在优势的原因就在于它的层次表示和抽象，使得其学习能力更加的强大。