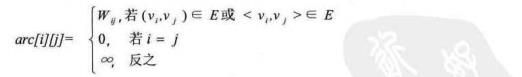图的定义和存储结构
学习目的及应用:导航 、GPS、网络规划、路径规划
交通流可以用一个图来模型化,每一条街道交叉口表示一个顶点,而每一条街道就是一条边。边的值可能是代表限制速度,或者是容量(车道的数目)等等。此时我们可能需要找出一条最短路,或用该信息找出最可能产生交通瓶颈的位置,
图的定义:
是由顶点的
有穷非空集合和顶点之间
边的集合组成一种数据结构
表示方法:
graph = ( V,E )
V = { x | x 属于 某个数据对象} 是顶点的有穷非空集合
E = { (x, y) | (x, y) 属于 V },顶点之间关系的有穷集合,也叫做边集合
顶点:即在图中数据元素
无向图与有向图的定义:
•无向图:任意两个顶点之间的边都是无向边。
无向边:顶点A和B之间的边没有方向,则称该边为无向边(A, B)
•有向图 :图中任意两个顶点之间的边均是有向边,也称为弧
有向边:顶点A和B之间的边有方向,则称该边为有向边< B, A>
度的定义:
顶点v的度是和 v 相关联的边的数目,记为TD(v).
•入度:以 v 为头的边的数目,记为ID(v)
•出度,以 v 为尾的边的数目,记为OD( v )
关于度的一些公式:
TD(v) = ID(v) + OD(v)
E = [ TD( v1) + TD( v2 ) + ... ] / 2
E = ID( v1) + ID( v2 ) + ... //入度之和
E = OD( v1) + OD( v2 ) + ... //出度之和
权的定义:
与图的边相关的数字叫做权。
•权常用来表示图中顶点间的距离或者耗费。
图的一些操作:
/*创建并返回n个顶点的图结构*/ Graph* graph_creat(int n); /*销毁图结构*/ void graph_destroy(Graph* graph); /*清空图结构*/ void graph_clear(Graph* graph); /*在图的顶点v1和v2之间增加权值为w的边*/ int graph_add_edge(Graph* graph, int v1, int v2, int w); /*删除顶点v1和v2的边,返回权值*/ int graph_remove_edge(Graph* graph, int v1, int v2); /*获得顶点v1和v2之间边的权值*/ int graph_get_edge(Graph* graph,int v1, int v2); /*返回顶点v的度*/ int graph_td(Graph* graph, int v); /*返回图的顶点的个数*/ int graph_vertex_count(Graph* graph); /*返回图中顶点的边数*/ int graph_edge_count(Graph* graph);
图的存储结构
一. 邻接矩阵法
基本思想:用两个数组来表示图
一个一维数组存储图中顶点信息
一个二维数组存储图中的边(弧)的信息
设图A = (V, E)是一个有n个顶点的图,图的邻接矩阵为arc[n][n],定义为:
关于邻接矩阵的头结点:
•记录顶点的个数
•记录与顶点相关的数据描述
•记录描述边集的二维数组
typedef struct {
int count;
m_vertex** v;
int** matrix;
}tm_graph;
实现的操作:
#include <stdio.h>
#include <malloc.h>
#include "graph.h"
/*头结点结构体*/
typedef struct {
int count;
m_vertex** v; //指向n个类型为(m_vertex *)的指针区域。该区域的指针指向记录结点信息的内存
int** matrix;
} tm_graph;
MGraph* graph_creat(m_vertex** v, int n)
{
tm_graph* ret = NULL;
if((v != NULL) && (n > 0))
{
ret = (tm_graph*)malloc( sizeof(tm_graph) );
if(ret != NULL)
{
int i = 0;
int *p = NULL;
ret->count = n;
ret->v = (m_vertex**)malloc(sizeof(m_vertex *) *n);
/*申请一维地址空间*/
ret->matrix = (int**)malloc(sizeof(int*) * n);
/*申请一维数据空间,使用calloc可以把邻接矩阵清空,初始化为0*/
//p = (int*)malloc(sizeof(int) * n * n);
p = (int *)calloc(n * n, sizeof(int));
if( (ret->v != NULL) && (ret->matrix != NULL) && (p != NULL))
{
for(i=0; i < n; i++)
{
/*保存指向顶点数据的指针*/
ret->v[i] = v[i];
/*将数据空间与地址空间相连接*/
ret->matrix[i] = (p + i * n);
}
}
else
{
free(ret->v);
free(ret->matrix);
free(p);
}
}
}
return ret;
}
void graph_destroy(MGraph* graph)
{
tm_graph* t_graph = (tm_graph*)graph;
if(t_graph != NULL)
{
free(t_graph->v);
/*注:以下两步释放的顺序不能换*/
free(t_graph->matrix[0]);
free(t_graph->matrix);
free(t_graph);
}
}
/*清空图结构*/
void graph_clear(MGraph* graph)
{
tm_graph* t_graph = (tm_graph*)graph;
if(t_graph != NULL)
{
int i = 0;
int j = 0;
for(i=0; i < t_graph->count; i++)
{
for(j=0; j < t_graph->count; j++)
{
t_graph->matrix[i][j] = 0;
}
}
}
}
/*在图的顶点v1和v2之间增加权值为w的边*/
int graph_add_edge(MGraph* graph, int v1, int v2, int w)
{
tm_graph* t_graph = (tm_graph*)graph;
int ret = 0;
ret = (t_graph != NULL) && (v1 >= 0) && (v1 < t_graph->count);
ret = (ret) && (v1 >= 0) && (v1 < t_graph->count);
ret = (ret) && (w >= 0);
if(ret)
{
t_graph->matrix[v1][v2] = w;
}
return ret;
}
/*删除顶点v1和v2的边,返回权值*/
int graph_remove_edge(MGraph* graph, int v1, int v2)
{
tm_graph* t_graph = (tm_graph*)graph;
int ret = 0;
ret = (t_graph != NULL) && (v1 > 0) && (v1 < t_graph->count);
ret = (ret) && (v1 > 0) && (v1 < t_graph->count);
if(ret)
{
ret = t_graph->matrix[v1][v2];
t_graph->matrix[v1][v2] = 0;
}
}
/*获得顶点v1和v2之间边的权值*/
int graph_get_edge(MGraph* graph,int v1, int v2)
{
tm_graph* t_graph = (tm_graph*)graph;
int ret = 0;
ret = (t_graph != NULL) && (v1 > 0) && (v1 < t_graph->count);
ret = (ret) && (v1 > 0) && (v1 < t_graph->count);
if(ret)
{
ret = t_graph->matrix[v1][v2];
}
return ret;
}
/*返回顶点v的度*/
int graph_td(MGraph* graph, int v)
{
tm_graph* t_graph = (tm_graph*)graph;
int ret = 0;
if(t_graph != NULL)
{
int i = 0;
/*出度*/
for(i=0; i<t_graph->count; i++)
{
if(t_graph->matrix[v][i] != 0)
{
ret++;
}
}
/*入度*/
for(i=0; i<t_graph->count; i++)
{
if(t_graph->matrix[i][v] != 0)
{
ret++;
}
}
}
return ret;
}
/*返回图的顶点的个数*/
int graph_vertex_count(MGraph* graph)
{
tm_graph* t_graph = (tm_graph*)graph;
int ret = 0;
if(t_graph != NULL)
{
ret = t_graph->count;
}
}
/*返回图中顶点的边数*/
int graph_edge_count(MGraph* graph)
{
tm_graph* t_graph = (tm_graph*)graph;
int ret = 0;
if(t_graph != NULL)
{
int i = 0;
int j = 0;
for(i=0; i < t_graph->count; i++)
{
for(j=0; j < t_graph->count; j++)
{
if(t_graph->matrix[i][j] != 0)
{
ret++;
}
}
}
}
return ret;
}
void graph_display(MGraph* graph, graph_printf* p_func)
{
tm_graph* t_graph = (tm_graph*)graph;
int ret = 0;
if((t_graph != NULL) && (p_func != NULL))
{
int i = 0;
int j = 0;
/*打印结点*/
for(i=0; i<t_graph->count; i++)
{
printf("%d", i);
printf(",");
p_func(t_graph->v[i]);
printf(" ");
}
/*打印边*/
for(i=0; i<t_graph->count; i++)
{
for(j=0; j<t_graph->count; j++)
{
if(t_graph->matrix[i][j] != 0)
{
printf("<");
p_func(t_graph->v[i]);
printf(", ");
p_func(t_graph->v[j]);
printf(", ");
printf("%d", t_graph->matrix[i][j]);
printf(">");
printf(" ");
}
}
}
}
}
缺点:对于边数相对于顶点较少的图,对存储空间会造成相当不必要的浪费。
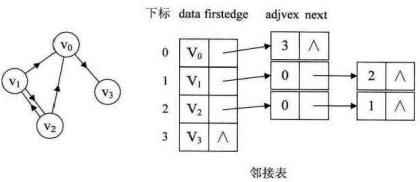
二、邻接链表法
( 避免了空间的浪费 )
基本思想:
•从同一个顶点发出的边 链接 在同一个链表中
•每个链表结点代表一条边,结点中保存边的另一顶点的下标和权值
邻接链表的头结点
•记录顶点个数
•记录与顶点相关的数据描述
•记录描述边集的链表数组
typedef struct {
int count;
l_vertex** v;
LinkList** la;
}
实现的操作:
#include <stdio.h>
#include <malloc.h>
#include "LinkList.h"
#include "l_graph.h"
typedef void LGraph;
typedef void l_vertex;
typedef struct {
int count;
l_vertex** v;
LinkList** la;
}tl_graph;
typedef struct {
LinkListNode header;
int v;
int w;
}t_list_node;
/*创建并返回n个顶点的图结构*/
LGraph* graph_creat(l_vertex** v, int n)//O(n)
{
tl_graph* ret = NULL;
int ok = 1;
if((v != NULL) && (n > 0))
{
ret = (tl_graph*)malloc( sizeof(tl_graph) );
if(ret != NULL)
{
ret->count = n;
ret->v = (l_vertex**)calloc(n, sizeof(l_vertex*));
ret->la = (LinkList**)calloc(n, sizeof(LinkList*));
ok = (ret->v != NULL) && (ret->la != NULL);
if(ok)
{
int i = 0;
for(i=0; i<n; i++)
{
ret->v[i] = v[i];
}
/*注意此处对创建链表返回值的监测*/
for(i=0; (i<n) && ok ; i++)
{
ok = ok && ((ret->la[i] = LinkList_Create()) != NULL);
}
}
/*不成功分别对应两种情况
1、结点数据指针的空间或存储链表指针的指针数组的空间未申请成功
2、创建链表不成功*/
if(!ok)
{
if( ret->la != NULL)
{
int i=0;
for(i=0; i<n; i++)
{
LinkList_Destroy(ret->la[i]);
}
}
free(ret->la);
free(ret->v);
free(ret);
ret = NULL;
}
}
}
return ret;
}
/*销毁图结构*/
void graph_destroy(LGraph* graph)//O(n)
{
tl_graph* t_graph = (tl_graph*)graph;
if(t_graph != NULL)
{
int i = 0;
for(i=0; i<t_graph->count; i++)
{
LinkList_Destroy(t_graph->la[i]);
}
free(t_graph->la);
free(t_graph->v);
free(t_graph);
}
}
/*清空图结构*/
void graph_clear(LGraph* graph)
{
tl_graph* t_graph = (tl_graph*)graph;
if(t_graph != NULL)
{
int i = 0;
int j = 0;
for(i=0; i<t_graph->count; i++)
{
for(j=0; j<LinkList_Length(t_graph->la[i]); j++)
{
free(LinkList_Delete(t_graph->la[i], 0));
}
}
}
}
/*在图的顶点v1和v2之间增加权值为w的边*/
int graph_add_edge(LGraph* graph, int v1, int v2, int w)//O(1)
{
tl_graph* t_graph = (tl_graph*)graph;
t_list_node* node = NULL;
int ret = 0;
ret = (t_graph != NULL);
ret = (ret) && (0 <= v1) && (v1 < t_graph->count);
ret = (ret) && (0 <= v2) && (v2 < t_graph->count);
ret = (ret) && (0 < w);
ret = (ret) && (node = (t_list_node*)malloc(sizeof(t_list_node)));
if(ret)
{
node->v = v2;
node->w = w;
LinkList_Insert(t_graph->la[v1], (LinkListNode*)node, 0);
}
return ret;
}
/*删除顶点v1和v2的边,返回权值*/
int graph_remove_edge(LGraph* graph, int v1, int v2)//O(n*n)
{
tl_graph* t_graph = (tl_graph*)graph;
int ret = 0;
ret = (t_graph != NULL);
ret = (ret) && (0 <= v1) && (v1 < t_graph->count);
ret = (ret) && (0 <= v2) && (v2 < t_graph->count);
if(ret)
{
int i = 0;
t_list_node* node = NULL;
for(i=0; i<LinkList_Length(t_graph->la[v1]); i++)
{
node = (t_list_node*)LinkList_Get(t_graph->la[v1], i);
if(node->v == v2)
{
ret = node->w;
LinkList_Delete(t_graph->la[v1], i);
free(node);
break;
}
}
}
return ret;
}
/*获得顶点v1和v2之间边的权值*/
int graph_get_edge(LGraph* graph,int v1, int v2) //O(n*n)
{
tl_graph* t_graph = (tl_graph*)graph;
int ret = 0;
ret = (t_graph != NULL);
ret = (ret) && (0 <= v1) && (v1 < t_graph->count);
ret = (ret) && (0 <= v2) && (v2 < t_graph->count);
if(ret)
{
int i = 0;
t_list_node* node = NULL;
for(i=0; i<LinkList_Length(t_graph->la[v1]); i++)
{
node = (t_list_node*)LinkList_Get(t_graph->la[v1], i);
if(node->v == v2)
{
ret = node->w;
break;
}
}
}
}
/*返回顶点v的度*/
int graph_td(LGraph* graph, int v)//O(n*n*n)
{
tl_graph* t_graph = (tl_graph*)graph;
int ret = 0 ;
if((t_graph != NULL) && (0 <= v) && (v < t_graph->count))
{
int i = 0;
int j = 0;
t_list_node* node = NULL;
/*入度*/
for(i=0; i < t_graph->count; i++)
{
for(j=0; j < LinkList_Length(t_graph->la[i]); j++)
{
node = (t_list_node*)LinkList_Get(t_graph->la[i], j);
if(node->v == v)
{
ret++;
}
}
}
/*出度*/
for(i=0; i < LinkList_Length(t_graph->la[v]); i++)
{
ret++;
}
}
return ret;
}
/*返回图的顶点的个数*/
int graph_vertex_count(LGraph* graph)//O(1)
{
tl_graph* t_graph = (tl_graph*)graph;
int ret = 0 ;
if(t_graph != NULL)
{
ret = t_graph->count;
}
return ret;
}
/*返回图的边数*/
int graph_edge_count(LGraph* graph)//O(n)
{
tl_graph* t_graph = (tl_graph*) graph;
int ret = 0;
if(t_graph != NULL)
{
int i = 0;
int j = 0;
for(i=0; i < t_graph->count; i++)
{
ret += LinkList_Length(t_graph->la[i]);
}
}
return ret;
}
void graph_display(LGraph* graph, graph_printf* p_func)//O(n*n*n)
{
tl_graph* t_graph = (tl_graph*)graph;
int ret = 0;
if((t_graph != NULL) && (p_func != NULL))
{
int i = 0;
int j = 0;
t_list_node* node = NULL;
/*打印结点*/
for(i=0; i<t_graph->count; i++)
{
printf("%d", i);
printf(",");
p_func(t_graph->v[i]);
printf(" ");
}
printf("\n");
/*打印边*/
for(i=0; i<t_graph->count; i++)
{
for(j=0; j<LinkList_Length(t_graph->la[i]); j++)
{
node = (t_list_node*)LinkList_Get(t_graph->la[i], j);
printf("<");
p_func(t_graph->v[i]);
printf(", ");
p_func(t_graph->v[node->v]);
printf(", ");
printf("%d", node->w);
printf(">");
printf(" ");
}
}
printf("\n");
}
}
虽然邻接表的方法解决了空间浪费的问题,但是有些函数的时间复杂度却增加了。相当于利用时间换算了空间。
可根据项目的特性对以上两种图的存储结构进行选择。
注:
在为顶点的链表申请空间时,注意检查申请的空间是否成功。若有一个顶点的边链表没申请成功,则图的创建就没有成功,需要将申请好的链表释放掉
时间复杂度的分析
图的存储结构还有其他的方式:
譬如说:
十字链表(实际上十字链表就是把邻接链表(易于统计出度)和逆邻接链表(易于统计入度)相结合)
: 邻接多重表:
边集数组
( 两个一维数组,一个存储顶点的信息,一个存储边的信息)
C语言知识补充:
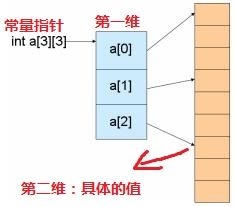
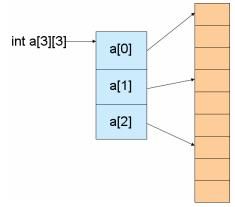
1、二维数组的实现原理
二维数组在内存中以一维的方式排布
二维数组中的第一维是一维数组
二维数组中的第二维才是具体的值
二维数组的数组名可看做常量指针
对于一维数组int a[5]来说,数组名a代表数组的首元素的地址, 注意此处强调a为地址,即指针
所以
a的类型为int *;
同样二维数组名同样代表数组首元素的地址,
则对于 int m[2][5]来讲,
数组名m的类型为 int( *)[5]
2、以指针方式遍历二维数组 a[i][j]
分析 将a[i]看做数组名,以指针下标的方式访问,则可表示为
*(a[i] + j);然后将其中的a[i]展开,即
*(*(a + i) + j);
实现代码:
#include <stdio.h>
int main(int argc, char* argv[], char* env[])
{
int a[3][3] = {{0, 1, 2}, {3, 4, 5}, {6, 7, 8}};
int i = 0;
int j = 0;
for(i=0; i<3; i++)
{
for(j=0; j<3; j++)
{
printf("%d\n", *(*(a+i) + j));
}
}
}
3、动态申请二维数组
可知二维数组在内存中也是线性方式存储的,
思考:
关于多维数组与多维指针的总结:
C中
只有一维数组,而且数组的大小必须在编译期即作为常数确定
C中的
数组元素可以是任何类型的数据,即数组的元素可以是另一个数组
C中
只有数组的大小和数组首元素的地址是编译器直接确定的。
4、使用calloc申请动态空间
calloc原型:
void *calloc(size_t num_elements, size_t element_size);
参数说明:
num_elements : 所需元素的数量
element_size : 每个元素的字节数
与malloc的区别:
calloc在返回指向内存的指针之前把它初始化为0,还有就是请求内存数量的方式不同。