第0周周赛——极限手速赛(题解)之下篇
J题:
J题题目链接
题目描述:
给定一个数n,问你在[1,n]之间有多少个数能够整除[2,10]中所有的数(对,你没看错,是所有哦)
输入只有一行,包含一个整数n (1 ≤ n ≤ 1018)
输出一个整数,表示在[1,n]之间有多少个数能够整除[2,10]中所有的数
3000
1
首先,要整除[2,10]中所有的数,那么我们必然想到,最小的能够整除[2,10]中所有的数是多大?
要整除[2,10]中所有的数,那么[2,10]中所有的数必然是该数的因子,而2是4的因子,4又是8的因子,3是9的因子,那么能够整除8也必然能够整除2和4,9也亦然,所以呢,要整除[2,10]中所有的数,那么该数必然含有因子5,7,8,9.则最小的能够整除[2,10]中所有的数是2520.
因此呢,要问在[1,n]中有多少个数能够整除[2,10]中所有的数,由于最小的能够整除[2,10]中所有的数是2520.那么要整除[2,10]中所有的数,必然是2520的整数倍的数。所以我们可以将问题转化为数字n"含有“多少个2520求解。
完整代码实现:
#include<cstdio>
#include<algorithm>
typedef unsigned long long ull;
int main()
{
ull n;
while(scanf("%I64u",&n)==1&&n)
{
printf("%I64u\n",n/2520);
}
return 0;
}
K题:
K题题目链接
给定一个数n,问你在[1,n]之间有多少个数对区间[2,10]中所有的数取余均不为0(对,你没看错,又是所有哦)
输入只有一行,包含一个整数n (1 ≤ n ≤ 1018)
输出一个整数,表示在[1,n]之间有多少个数对区间[2,10]中所有的数取余均不为0
12
2
解析:
要求在区间[1,n]之间有多少个数对区间[2,10]中所有的数取余均不为0,首先我们要知道的是,什么样的数对区间[2,10]中所有的数取余均不为0?首先,我们分析一下[2,10]中这些数。(前面是数本身,而后面是数的因子(1除外))
2:2;
3:3;
4:2,4;
5:5;
6:2,3,6;
7:7;
8:2,4,8;
9:3,9;
10:2,5,10;
那么如果一个数对区间[2,10]中所有的数取余均不为0,那么这个数的因子只要不含有[2,10]能够涵盖所有数中的公共因子即可,即这个数必须要对2,3,5,7取余均不为0即可。所以你可能想到答案不就出来了吗?直接用n-n/2-n/3-n/5-n/7不就好了?
但是这样得出来的是正确答案吗?显而易见是错误的。
原因是:举个例子吧,比如说数字6 (既能够整除2,又能够整除3,如果按照上述计算方式,数字6的话不就被计算两次了,也就是被多减了一次),所以呢,其实我们很快就发现其实这是一道容斥原理的题目
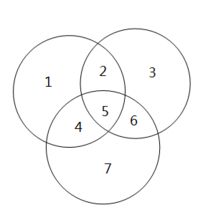
容斥原理的Venn图表示为:
![]()
证明过程详见百度百科:
容斥原理
因此最后结果即为:
ans=n-[n/2]-[n/3]-[n/5]-[n/7]+[n/6]+[n/10]+[n/14]+[n/15]+[n/21]+[n/35]-[n/30]-[n/42]–[n/70]-[n/105]+[n/210]
有两篇讲容斥原理比较好的文章:
【组合数学_容斥原理专辑】
容斥原理(翻译)
完整代码实现:
#include<cstdio>
using namespace std;
typedef long long ll;
int main()
{
ll n;
while(scanf("%I64d",&n)==1&&n)
{
ll ans=n-n/2-n/3-n/5-n/7+n/6+n/10+n/14+n/15+n/21+n/35-n/30-n/42-n/70-n/105+n/210;
printf("%I64d\n",ans);
}
return 0;
}
L题:
L题题目链接
给你一个五位数,然后将这个五位数按照<第一位> <第三位> <第五位> <第四位> <第二位>的顺序排列。再然后呢,将这个新得到的数字作x^5的幂运算,得到的数字取最后五位则是我们需要的答案,巴啦啦数学不好,你能帮她解决这个问题吗?(解决了上面的妹子就是你的了)
举例说明:
给定数字12345,先转换为13542,然后计算13542^5得到455 422 043 125 550 171 232,取最后五位71232输出
输入只有一行,包含一个五位数
输出一行,输出一个五位数
注意:00000不得输出0
12345
71232
这道题其实是一道基础数论的试题,我们需要知道一个结论:
(a*b) % m = ((a%m) * (b%m)) % m
所以呢,由此结论引申出另外一个结论:
(a1a2a3⋯an)%m=((a1%m)(a2%m)(a3%m)⋯(an%m))%m
那么这道题就迎刃而解了,这道题其实就是求(n^5)%100000,根据以上公式可直接求得,注意当后五位数均为0的时候应该输出0,所以输出格式为%05I64d
下面是解释这个问题的比较好的两篇文章,以及一篇将输出格式的文章
a的n次方对m取余
求 a的b次方对c求余 的结果
C语言printf()函数:格式化输出函数
完整代码实现:
#include<cstdio>
#include<algorithm>
typedef long long ll;
int main()
{
ll n;
while(scanf("%I64d",&n)==1)
{
ll change_n = n/10000*10000+n/100%10*1000+n%10*100+n/10%10*10+n/1000%10;
//printf("%I64d\n",change_n);
printf("%05I64d\n",(change_n%100000*change_n%100000*change_n%100000*change_n%100000*change_n%100000)%100000);
}
return 0;
}
M题:
M题题目链接
题目描述:
输入只有一行包含三个整数a, b, c ( - 1000 ≤ a, b, c ≤ 1000) — 表示方程ax2 + bx + c = 0的系数.
方程保证有两个不相等的实根
输出有两行,第一行是大根,第二行是小根.与答案相对误差不超过10 - 6视为正确.
1 30 200
-10.000000000000000
-20.000000000000000
这道题也属于签到题系列,直接调用一元二次方程求根公式即可
注意一下a,b,c的取值范围即可。
完整代码实现:
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
int main()
{
int a,b,c;
while(scanf("%d %d %d",&a,&b,&c)==3)
{
double x1 = (-b + sqrt(b*b-4*a*c)) / (2*a);
double x2 = (-b - sqrt(b*b-4*a*c)) / (2*a);
printf("%.20f\n%.20f\n",max(x1,x2),min(x1,x2));
}
return 0;
}
N题:
N题题目链接
题目描述:
输入只有一行,包含三个整数l3, l4, l5 (1 ≤ l3, l4, l5 ≤ 1000) — 分别对应三角形,正方形和正五边形的边长
输出一个数 - 金字塔的总体积。绝对或相对误差不应大于10 - 9.
2 5 3
38.546168065709
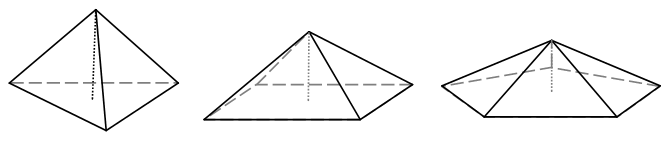
这道题本意则是求正n棱锥的体积。(特殊的正n棱锥,所有棱长都相等的)所以我们可以试着分析一下这道题。首先从棱锥的体积公式入手,无论什么样的棱锥,体积公式均为V = 1/3*S*h
首先我们要了解一下正n棱锥的一些性质:(摘自百度百科)
1.正n棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形;
2.正n棱锥顶点在底部的射影为底部的中心。
所以我们求得底面积和高即可求出正n棱锥的体积。
首先是正n棱锥的底面积,由于是正n棱锥,那么底面积均为正多边形,而为了总结出正n棱锥的底面积的一般规律,我们可以以其底面中心为顶点,外接圆的半径为腰长,将其底面切割成若干个全等的等腰三角形。
正三角形可以分解成三个顶角为120°的等腰三角形,而这等腰三角形的面积可用正弦定理求得1/2*r*r*sin120°,因此底面积为3*1/2*r*r*sin120°
正方形可以分解成四个顶角为90°的等腰直角三角形,而这等腰三角形的面积可用正弦定理求得1/2*r*r*sin90°,因此底面积为4*1/2*r*r*sin90°
正五边形可以分解成五个顶角为72°的等腰三角形,而这等腰三角形的面积可用正弦定理求得1/2*r*r*sin72°,因此底面积为5*1/2*r*r*sin72°
因此我们通过这里可以总结出一般规律
正n边形可以分解成n个顶角为360°/n的等腰三角形,面积为n*1/2*r*r*sin(360°/n);
那么外接圆的半径要怎么求解呢?
只要通过三角关系即可,因为已知棱长为l,所以可通过任意一个切割成的等腰三角形,可求得r = l/2/sin(180°/n);
所以呢,到这里,底面积就已经求好了,那么高呢?根据性质1,只需要通过勾股定理求解就好了
因此有h = sqrt(l^2-r^2)
程序中注意sin,cos函数的形参都是弧度制的
完整代码实现:
#include<cstdio>
#include<algorithm>
#include<cmath>
const double PI = acos(-1.0);
double volume(double l,int n);
int main()
{
double l1,l2,l3;
while(scanf("%lf%lf%lf",&l1,&l2,&l3)==3)
{
printf("%.12f\n",volume(l1,3)+volume(l2,4)+volume(l3,5));
}
return 0;
}
double volume(double l,int n) //l表示边长,n表示几边形
{
double r = l / 2 / sin(PI/n);
double h = sqrt(l*l-r*r);
return n*r*r/2*sin(2*PI/n)*h/3;
}
O题:
O题题目链接
题目描述:
给定一个整数n, 找到最小的正整数x使得2^x mod n = 1.
输入只有一行,包含一个整数n(n的值不超过int的最大值)
如果x存在,则输出一行2^x mod n = 1.
否则的话则输出2^? mod n = 1.
你应该将x 和 n替换成实际的数字
2 5
2^? mod 2 = 1 2^4 mod 5 = 1
找到最小的正整数x,使得2^xmodn=1,首先我们从数字n的角度考虑,由于除数2^x恒为偶数(2,4,8,...),那么很明显当n小于等于1和当n为偶数时,是不可能得到为1的余数的,所以我们可以先用一个if条件判断语句,如果n满足上述条件的话,则直接输出2^? mod n = 1
然后由欧拉定理可知:(摘自百度百科)
欧拉定理
若n,a为正整数,且n,a互质,那么必然存在数x,使得a^x%n=1,由于剩下的只有n为奇数的情况,而且幂运算的底数2与n互质,所以我们只需要暴力枚举就好了。
在暴力枚举的时候要注意对2^x取余,防止数据过大
即(a*b)% c = ((a%c)* (b%c))% c;
由于是这道题数据量可能比较弱,所以这样做就过了,然后我在网上也搜到了一遍比较好的详细分析这道题的文章
HDU 1395 2^x mod n = 1-[解题报告]
完整代码实现:
#include<cstdio>
int main()
{
int n;
while(scanf("%d",&n)==1){
if(n%2==0||n<=1)
printf("2^? mod %d = 1\n",n);
else{
int s = 1;
for(int i = 1;;i++){
s*=2;
if(s%n==1){
printf("2^%d mod %d = 1\n",i,n);
break;
}
s = s % n;
}
}
}
return 0;
}
P题:
P题题目链接
题目描述:
There is a legend in the IT City college. A student that failed to answer all questions on the game theory exam is given one more chance by his professor. The student has to play a game with the professor.
The game is played on a square field consisting of n × n cells. Initially all cells are empty. On each turn a player chooses and paint an empty cell that has no common sides with previously painted cells. Adjacent corner of painted cells is allowed. On the next turn another player does the same, then the first one and so on. The player with no cells to paint on his turn loses.
The professor have chosen the field size n and allowed the student to choose to be the first or the second player in the game. What should the student choose to win the game? Both players play optimally.
The only line of the input contains one integer n (1 ≤ n ≤ 1018) — the size of the field.
Output number 1, if the player making the first turn wins when both players play optimally, otherwise print number 2.
1
1
2
2
题目大意:
在一个n*n的棋盘上轮流下棋,初始时棋盘全空,每次只能在空格上下棋,而且此空格上下左右不能有棋子,但是对角可以有棋子,最后谁无棋可下谁输。假设下棋的两者都足够机智(意思就是说都能下在此时对自己最有利的位置),现给出棋盘大小,如果先手赢则输出1,否则输出2
解析:
个人觉得这是一道简单博弈论的题目,首先我们从简单的开始分析,然后总结出一般规律。
1.首先如果棋盘大小为1*1的时候,由于只有一个空位,那么先手是必赢的,输出1
2. 如果棋盘大小为2*2的时候,共有四个空位,无论先手是下在什么位置,后手能下在其对角的位置,然后再轮到先手时,先手无位置可下棋,所以此时为后手赢,输出2
3.如果棋盘大小为3*3的时候,共有九个空位,由于题设给出下棋的两者都足够机智,那么这时候先手最有利的位置便是棋盘中央,然后后手只能下在先手下的位置所在的对角线上,而再次轮到先手,先手便可以下在后手所下位置关于棋盘中心对称对称的位置,而后依旧这样,最后一定是后手无棋可下(可枚举情况)
所以呢:
如果n为奇数,那么先手第一步将棋子下在正中,那么之后无论后手下哪儿,先手都可以将棋下在与后手上一步棋关于棋盘中心对称对称的位置,最后一定是后手无棋可下,此时输出1(直到各个对角线上无位置可下棋);如果n为偶数,那么无论先手下哪儿,后手都可以将棋下在与先手上一步棋关于棋盘中心对称的位置,最后一定是先手无棋可下,此时输出2
有一篇讲acm常用的博弈论比较好的文章:
博弈论——acm
完整代码实现:
#include<cstdio>
#include<algorithm>
typedef unsigned long long ull;
int main()
{
ull n;
while(scanf("%I64u",&n)==1&&n)
{
if(n%2==0)
printf("2\n");
else
printf("1\n");
}
return 0;
}
总结下:要善于对数学问题进行建模,并且记住而且要会推导常用的数学结论,如欧拉定理,容斥原理等一些常用的数学知识。