hdu1452 Happy 2004(规律+因子和+积性函数)
Happy 2004
题意:s为2004^x的因子和,求s%29. (题于文末)
知识点:
素因子分解:n = p1 ^ e1 * p2 ^ e2 *..........*pn ^ en
因子和: Sum=(p1^0+p1^1….p1^e1)*(p2^0+p2^1…p2^e2)……(pn^0+…pn^en)
=;
积性函数:s(xy)=s(x)*s(y) (比如:幂函数,因子和,欧拉函数,莫比乌斯函数)
对于正整数n的一个算术函数 f(n),若f(1)=1,且当a,b互质时f(ab)=f(a)f(b),在数论上就称它为积性函数。
若对于某积性函数 f(n),就算a, b不互质,也有f(ab)=f(a)f(b),则称它为完全积性的。
题解:
一般模值(mod)较小时会有规律,可以找下循环节。
发现答案的循环结为28.
#include<iostream>
using namespace std;
int a[]={6,16,8,10,25,7,14,3,23,17,13,17,0,27,7,14,15,17,26,26,20,17,9,22,22,23,0,1};
int main()
{
int x;
while(cin>>x&&x)
{
cout<<a[(x-1)%28]<<endl;
}
/*找规律过程
for(x=1;x<=100;x++)
{
int a2=1,a3=1,a167=1,ans2=0,ans3=0,ans167=0;
for(int i=0;i<=x*2;i++)
{
ans2+=a2;
a2*=2;
ans2%=29;
a2%=29;
}
for(int i=0;i<=x;i++)
{
ans3+=a3;
a3*=3;
ans3%=29;
a3%=29;
}
for(int i=0;i<=x;i++)
{
ans167+=a167;
a167*=167;
ans167%=29;
a167%=29;
}
cout<<ans2*ans3*ans167%29<<endl;
}*/
return 0;
}
再给出一般解:
因子和为积性函数,so sum(2004^X)= sum(2^2X) * sum(3^X)* sum(167^X)
sum(2004^X)%29=sum(2^2X) %29 * sum(3^X)%29 * sum(167^X)%29
=sum((2%29)^2X) %29 * sum((3%29)^X)%29 * sum((167%29)^X)%29
=sum(2^2X) * sum(3^X) * sum(22^X)%29
2的逆元是15 ,21的逆元是18
=((2^(2X+1)-1)* (3^(X+1)-1)*15 *(22^(X+1)-1)*18)%29
快速幂取模,实现2^2x,3^x,22^x O(logn)的运算
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
int quick_mod(int a,int n )
{
int b = 1;
while( n > 1 )
if( n % 2 == 0 )
{
a = ( a * a ) % 29;
n /= 2;
}
else
{
b = b * a % 29;
n--;
}
return a * b % 29;
}
int main()
{
int X;
int a, b, c;
while(scanf("%d",&X), X )
{
a = quick_mod( 2, 2 * X + 1 );
b = quick_mod( 3, ( X + 1 ) );
c = quick_mod( 22, ( X + 1 ) );
printf("%d\n",( a - 1 ) * (( b - 1 ) * 15) * ( c - 1 ) * 18 % 29) ;
}
return 0;
}
全题:
Happy 2004
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Submit Status
Description
Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your job is to determine S modulo 29 (the rest of the division of S by 29).
Take X = 1 for an example. The positive integer divisors of 2004^1 are 1, 2, 3, 4, 6, 12, 167, 334, 501, 668, 1002 and 2004. Therefore S = 4704 and S modulo 29 is equal to 6.
Input
The input consists of several test cases. Each test case contains a line with the integer X (1 <= X <= 10000000).
A test case of X = 0 indicates the end of input, and should not be processed.
Output
For each test case, in a separate line, please output the result of S modulo 29.
Sample Input
1 10000 0
Sample Output
6 10
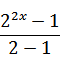
![clip_image002[4] clip_image002[4]](http://img.e-com-net.com/image/info5/49bcf6a82078418a88bfb975ed98c040.png)
![clip_image002[12] clip_image002[12]](http://img.e-com-net.com/image/info5/b20e8ce43e8d494aa7037a862f7405a3.png)