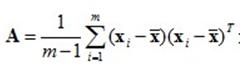机器学习降维算法一：PCA (Principal Component Analysis)

http://www.cnblogs.com/xbinworld/archive/2011/11/24/pca.html

言：

机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。

当然还有一大类方法本质上也是做了降维，叫做feature selection，目的是从原始的数据feature集合中挑选一部分作为数据的表达。

目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据。

之所以使用降维后的数据表示是因为:

(1)在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维,我们希望减少冗余信息所造成的误差,提高识别（或其他应用）的精度。

(2)或者希望通过降维算法来寻找数据内部的本质结构特征。

(3)通过降维来加速后续计算的速度

(4)还有其他很多目的，如解决数据的sparse问题

在很多算法中，降维算法成为了数据预处理的一部分，如PCA。事实上，有一些算法如果没有降维预处理，其实是很难得到很好的效果的。

如果你需要处理数据，但是数据原来的属性又不一定需要全部保留，那么PCA也许是一个选择。

 

主成分分析算法（PCA）

Principal Component Analysis(PCA)是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。

通俗的理解，如果把所有的点都映射到一起，那么几乎所有的信息（如点和点之间的距离关系）都丢失了，而如果映射后方差尽可能的大，那么数据点则会分散开来，以此来保留更多的信息。可以证明，PCA是丢失原始数据信息最少的一种线性降维方式。（实际上就是最接近原始数据，但是PCA并不试图去探索数据内在结构）

设n维向量w为目标子空间的一个坐标轴方向（称为映射向量），最大化数据映射后的方差，有：

其中m是数据实例的个数， xi是数据实例i的向量表达， x拔是所有数据实例的平均向量。定义W为包含所有映射向量为列向量的矩阵，经过线性代数变换，可以得到如下优化目标函数：

   W'W=I是说希望结果的每一个feature都正交，这样每一维度之间不会有冗余信息。

 

 其中tr表示矩阵的迹，A是数据协方差矩阵。

容易得到最优的W是由数据协方差矩阵前k个最大的特征值对应的特征向量作为列向量构成的。这些特征向量形成一组正交基并且最好地保留了数据中的信息。

PCA的输出就是Y = W'X，由X的原始维度降低到了k维。因此不知道推导也无所谓，只要会算就行，注意X需要均值化。

来看个例子：

 

当使用1个特征向量的时候，3的基本轮廓已经保留下来了，特征向量使用的越多就越与原始数据接近

   

PCA追求的是在降维之后能够最大化保持数据的内在信息，并通过衡量在投影方向上的数据方差的大小来衡量该方向的重要性。但是这样投影以后对数据的区分作用并不大，反而可能使得数据点揉杂在一起无法区分。这也是PCA存在的最大一个问题，这导致使用PCA在很多情况下的分类效果并不好。具体可以看下图所示，若使用PCA将数据点投影至一维空间上时，PCA会选择2轴，这使得原本很容易区分的两簇点被揉杂在一起变得无法区分；而这时若选择1轴将会得到很好的区分结果。

   

Discriminant Analysis所追求的目标与PCA不同，不是希望保持数据最多的信息，而是希望数据在降维后能够很容易地被区分开来。后面会介绍LDA的方法，是另一种常见的线性降维方法。另外一些非线性的降维方法利用数据点的局部性质，也可以做到比较好地区分结果，例如LLE，Laplacian Eigenmap等。以后会介绍。