第四周周赛——我查,我查,我查查查题解(来自poj2524,1664,1182,HDU1021,5524,5645)
A题:
A题题目链接
题目描述:
Ubiquitous Religions
You know that there are n students in your university (0 < n <= 50000). It is infeasible for you to ask every student their religious beliefs. Furthermore, many students are not comfortable expressing their beliefs. One way to avoid these problems is to ask m (0 <= m <= n(n-1)/2) pairs of students and ask them whether they believe in the same religion (e.g. they may know if they both attend the same church). From this data, you may not know what each person believes in, but you can get an idea of the upper bound of how many different religions can be possibly represented on campus. You may assume that each student subscribes to at most one religion.
10 9 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 10 4 2 3 4 5 4 8 5 8 0 0
Case 1: 1 Case 2: 7
给定n,m,分别表示学生总人数和宗教关系总数,然后接下来m行,给出m行数据,每行两个整数,表示这两个学生的宗教信仰是相同的,最后要求输
出在这n个学生中,最多有多少种宗教信仰?
解析:
这是一道典型的基础并查集的题目,首先我们看第二组测试数据:
10 4
2 3
4 5
4 8
5 8
一开始的时候这10个同学各自是一个集合,即10个同学各自无关系:
{1},{2},{3} ,{4} ,{5} ,{6} ,{7} ,{8} ,{9} ,{10}
第一组是2 3,表示学生2和学生3的宗教信仰相同,由于2,3不属于同一个集合,则将这两个元素归入同一个集合{2,3}
然后是第二组数据 4 5,同样的由于4,5不属于同一个集合,那么将这两个元素归入同一个集合{4,5}
接下来是4 8,4,8不属于同一个集合,那么将4,8归入同一个集合,而原来元素4在集合{4,5}中,所以这时候集合变为{4,5,8}
按照同样的方式处理后续数据,那么最终剩下的几个集合(每个集合可以看成一棵单独的有根树)为:
{1},{2,3},{4,5,8},{6},{7},{9},{10}
因此最后的宗教信仰总数为7种。
完整代码实现:
#include<stdio.h>
#define size 50010
int father[size],rank[size];
//并查集初始化操作
void Init(int N){
int i;
for(i = 1;i < N;++i){
father[i] = i;
rank[i] = 1; //father[i]用于记录节点i的父亲节点,而rank[i]则用于记录
//节点i作为根节点时整棵树的大小(也称权重,用于记录树的节点个数)
}
}
//寻找根节点并且压缩路径
int find_set(int node) {
if (father[node] != node) {
father[node] = find_set(father[node]);
}
return father[node];
}
//合并
int _union(int p,int q){
int root1 = find_set(p);
int root2 = find_set(q);
if(root1==root2){
return 0; //如果当前操作到的两个节点同属于一个连通分量(即是同一棵树中的节点)
//则不执行合并操作直接返回0,表示合并失败
}
if(rank[root1] > rank[root2]){
father[root2] = root1; //小树连接到大树上,并且权值加至合并后
//整棵完整的树的树根上
rank[root1] += rank[root2];
}
else{
father[root1] = root2;
rank[root2] += rank[root1];
}
return 1;
}
int main(){
int n, m, x, y,flag = 1;
while(scanf("%d %d",&n,&m)==2&&(n+m!=0)){
Init(size); //初始化操作
int count = n;
for(int i = 0;i < m;++i){
scanf("%d %d",&x,&y);
if(_union(x,y)){
--count;
}
}
printf("Case %d: %d\n",flag++,count);
}
return 0;
}
B题:
B题题目链接
题目描述:
斐波那契数列再现
定义: F(0) = 7, F(1) = 11, F(n) = F(n-1) + F(n-2) (n>=2).
输入一行,包含一个整数n (n < 1,000,000).
输出"yes" 如果 3 能够整除F(n).
否则的话输出"no".
0 1 2 3 4 5
no no yes no no no
刚开始拿到这道题的时候,由于题目的给的信息不是很丰富,所以一开始的时候可能会摸不着头脑,而且n的值却又很大,那么我们
可以先枚举去前30项(由于这道题数据比较大,所以枚举前30项防止数据溢出),看看是否能够找出什么规律,所以呢,这时候就是打表发挥作用
的时候了。我们可以先把前30项打表打出来:
通过打表,我们很快发现,从第三项开始,no和yes是四个一循环的。
因此得出以下完整代码:
#include<cstdio>
int main(){
int n;
while(scanf("%d",&n)!=EOF){
if((n-2)%4==0){
printf("yes\n");
}
else{
printf("no\n");
}
}
return 0;
}
其实这道题不找规律也是可以做的,因为10^6的数量级,在1s之内一般是不会超时的,但是到了50项之后,数据过大则会导致溢出,那么我们要怎么
办呢?还记得上次周赛的数据离散化的知识点吗?这道题我们关心的只是这个数是否是3的倍数,那么每一项保留3的余数部分不就可以了?如果这
一项3的余数部分是0的话,那么说明能够整除3,反之则不能。所以我们可以先预处理一下然后得出以下完整代码:
#include<cstdio>
const int maxn = int(1e6) + 10;
int a[maxn];
int main(){
int ans,n;
a[0] = 1,a[1] = 2;
for(int i = 2;i < maxn;++i){
ans = (a[i-2] + a[i-1]) % 3;
a[i] = ans;
}
while(scanf("%d",&n)!=EOF){
printf("%s\n",!a[n] ? "yes":"no");
}
return 0;
}
C题:
C题题目链接
题目描述:
T^T的苹果
有一天,T^T得到了一些苹果,他想把这些苹果都放到盘子里去。把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?(用K表示)5,1,1和1,5,1 是同一种分法。
1 7 3
8
解析:
C题数据量比较小..枚举的话小心一点很快就能出答案了,我就不把我的枚举代码拿出来了,这里有一份吴荣钦学长写的题解:
F - 小晴天老师系列——苹果大丰收
D题:
D题题目链接
题目描述:
T^T的概率论
T^T喜欢玩球(其实更喜欢ACM)。
他有n个球,装进一个大盒子里。每个球上面都写着一个整数。
有一天他打算从盒子中挑两个球出来。他先均匀随机地从盒子中挑出一个球,记为A。他不把A放回盒子,然后再从盒子中均匀随机地挑出一个球,记为B。
如果A上的数字严格大于B上的数字,那么他就会感到非常的happy。
现在告诉你每个球上的数字,请你求出他感到happy的概率是多少(让T^T开心真不容易(~ o ~)~zZ)。
第一行t,表示有t组数据。
接下来t组数据。每组数据中,第一行包含一个整数n,第二行包含n个用空格隔开的正整数ai,表示球上的数字。
(1≤t≤300,2≤n≤300,1≤ai≤300)
对于每个数据,输出一个实数答案,保留6位小数。
2 3 1 2 3 3 100 100 100
0.500000 0.000000
这题就是简单的求概率,由于n的数据范围很小,因此直接枚举出有多少对"A">"B",然后再除以总的情况即可,总的情况是n*(n-1)种
完整代码实现:
#include<cstdio>
const int maxn = 310;
int num[maxn];
int main(){
int t,n;
scanf("%d",&t);
while(t--){
scanf("%d",&n);
for(int i = 0;i < n;++i){
scanf("%d",&num[i]);
}
int ans = 0;
for(int i = 0;i < n;++i)
for(int j = 0;j < n;++j){
if(i == j){
continue;
}
else{
if(num[i] > num[j]){
++ans;
}
}
}
printf("%.6f\n",(double)ans/n/(n-1));
}
return 0;
}
E题:
E题题目链接
题目描述:
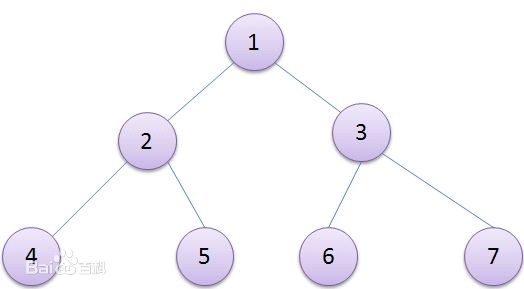
完全二叉树
一棵有N个节点的完全二叉树,问有多少种子树所含的节点数目不同?
输入有多组数据,不超过1000组.
每组数据输入一行包含一个整数N(1<=N<=10^18)
对于每组数据输出一行,表示不同节点数的子树有多少种.
5 6 7 8
3 4 3 5
解析:
(解题思路来自CSDN博客)
这道题要是对数据结构中树的考察,需要对树有比较深刻的理解,而且能够熟练的使用其中的概念。
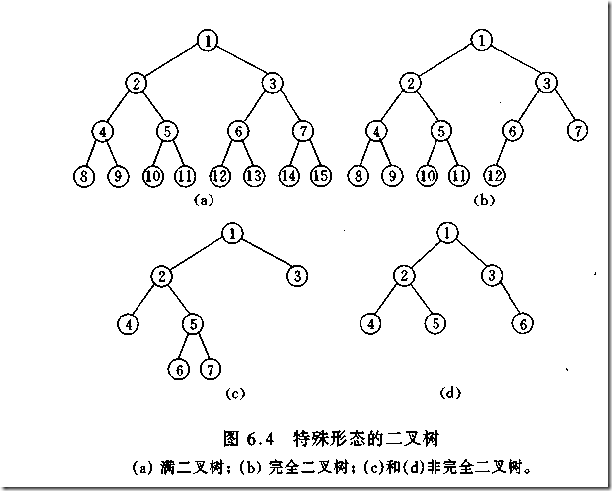
首先我们看给定的是一棵完全二叉树,那么对于一棵完全二叉树,其左右子树必然有一棵是满二叉树。我们可以首先从简单的部分
开始考虑:
1.完全二叉树是满二叉树的情况,在这种情况下,该完全二叉树的层数即是其子树的数量:
2.然后考虑非满二叉树的情况,非满二叉树又可以分成两种情况进行考虑:
(1).左子树是满二叉树的情况:
如下图图(b)
当左子树是满二叉树时,左子树满的层数比右子树多一层,因此左子树计算得子树数目+1,当该完全二叉树最后一层的节点数为奇
数时,那么右子树最后一层的节点数也为奇数,在这样的情况下,左右子树没有重复计算的相同节点的子树(奇偶不相同,可从图上
分析得出),那么将根的左右子树的总子树数目相加即可。而该完全二叉树最后一层的节点数为偶数时,那么从最后一层开始,左右子树存在
相同的子树部分,则要减掉重复的部分,那么我们便要从最后一层开始往上遍历,直到该层与上一层遍历过来的相关节点数目为奇数,记录此时的结
果(就想上图中的(b)图,如果最后一层的节点数为6时(即12旁边还有个编号13的节点),那么向上遍历一层至(4),(5),(6)节点,此时
相关节点数为3,那么停止遍历,其实在这一层的左子树节点数为7,右子树是5)
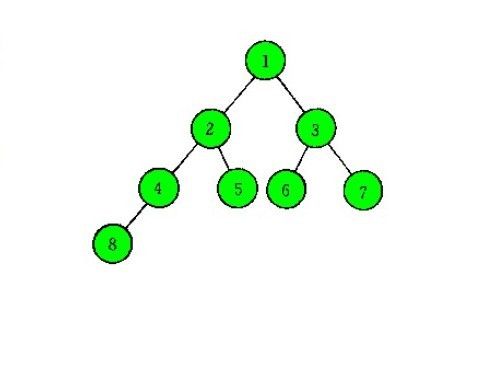
(2).右子树是满二叉树的情况:
同样的,当右子树是满二叉树时,左右子树满的层数相同,而后续处理过程与上述一样。
完整代码实现:
#include<cstdio>
#include<algorithm>
typedef long long LL;
const int maxn = 63;
LL f[maxn];
int main(){
LL i = 1,ans = 2;
f[0] = 0;
while(i < maxn){
f[i] = ans - 1;
++i;
ans <<= 1;
}
LL N;
while(scanf("%I64d",&N)==1&&N){
LL cnt = 0,tmp = N;
while(tmp){
++cnt;
tmp >>= 1;
}
//满二叉树的情况
if(f[cnt]==N){
printf("%I64d\n",cnt);
continue;
}
LL ans = cnt - 2;
LL l = N - f[cnt-1],r = f[cnt] - N;
//左子树为满二叉树的情况
if(l>=r){
++ans;
}
//右子树为满二叉树的情况
while(!(l&1) && --cnt){
l >>= 1;
}
//左子树+右子树+整棵树本身
printf("%I64d\n",ans + (cnt-2) + 1);
}
return 0;
}
F题:
F题题目链接
题目描述:
食物链
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。
100 7 1 101 1 2 1 2 2 2 3 2 3 3 1 1 3 2 3 1 1 5 5
3
解析:
F题这道题是《挑战程序设计竞赛》中并查集的例题,以下解题思路来自《挑战程序设计竞赛》
由于对于给定的动物序号我们无法确定它们属于A,B,C中的哪种动物,所以对于每只动物i创建3个元素i-A,i-B,i-C,并用3×N个元素建立并查集,并且维护如下信息:
1、i-X表示i属于X
2、如果i-A和j-B在同一个组里,那么如果i属于A,j就一定属于B。如果j属于B,i就一定属于A。
然后就是对每条信息的操作,分两种情况:
1.给定的两只动物x和y属于同一种类,如果给定的信息是x,y不在同一类,那么说明这是假话,则结果加1,然后我们将x-A和y-A,x-B和y-B,x-C和y-C合并
2.给定的两只动物x和y被吃关系(即x吃y),同样的,如果给定的信息是x,y在同一类,或者是x-A和y-C形成被吃关系的,都是假话,那么结果都将加1.然后我们将x-A和y-B,x-B和y-C,x-C和y-A合并
当然,在合并的时候再考虑是否在同一组,路径压缩,按秩优化等等问题
另外还有其他的解法:
【POJ1182】食物链,思路+数据+代码
完整代码实现:
#include<cstdio>
#include<algorithm>
const int max_k = int(2e5) + 10;
int father[max_k],rank[max_k],d[max_k],x[max_k],y[max_k];
int N,K;
//初始化
void Init(int n){
for(int i = 0;i < n;++i){
father[i] = i;
rank[i] = 1;
}
}
//寻找根节点并且路径压缩
int find_set(int node){
if(father[node] != node){
father[node] = find_set(father[node]);
}
return father[node];
}
//用来判断x,y是否同属于一棵有根树
bool same(int x,int y) {return find_set(x)==find_set(y);}
//联合两棵有根树
void union_node(int p,int q){
int root1 = find_set(p);
int root2 = find_set(q);
if(root1 == root2){
return; //同属于一棵有根树
}
if(rank[root1]>rank[root2]){ //根1权值更大
father[root2] = root1;
rank[root1] += rank[root2];
}
else{
father[root1] = root2;
rank[root2] += rank[root1];
}
}
void solve(){
int t,m,n,ans = 0;
Init(3*N); //并查集初始化
//m-A 范围为[0,N-1],m-B [N,2*N-1],m-C [2N,3*N-1]
for(int i = 0;i < K;++i){
t = d[i];
m = x[i]-1;
n = y[i]-1; //将编号变成0-N-1,方便程序运算
if(m<0 || m>=N || n<0 || n>=N){
++ans;
continue; //输入不合法的情况
}
//m,n两个是同类的情况下
if(t == 1){
if(same(m,n+N)||same(m,n+2*N)){
++ans;
}
else{
union_node(m,n);
union_node(m+N,n+N);
union_node(m+2*N,n+2*N);
}
}
//m吃n的情况
else{
if(same(m,n)||same(m,n+2*N)){
++ans;
}
else{
union_node(m,n+N);
union_node(m+N,n+2*N);
union_node(m+2*N,n);
}
}
}
printf("%d\n",ans);
}
int main(){
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
scanf("%d %d",&N,&K);
for(int i = 0;i < K;++i){
scanf("%d %d %d",&d[i],&x[i],&y[i]);
}
solve();
return 0;
}
总结:基础很重要,基础不牢固,做难题也是磕磕绊绊的,要先打牢基础,多充电,多涨知识。
如有错误和不足之处,还请指正,O(∩_∩)O谢谢