哈夫曼树和哈夫曼编码基本概念及构造

1.哈夫曼编码的起源：

哈夫曼编码是 1952 年由 David A. Huffman 提出的一种无损数据压缩的编码算法。哈夫曼编码先统计出每种字母在字符串里出现的频率，根据频率建立一棵路径带权的二叉树，也就是哈夫曼树，树上每个结点存储字母出现的频率，根结点到结点的路径即是字母的编码，频率高的字母使用较短的编码，频率低的字母使用较长的编码，使得编码后的字符串占用空间最小。

2.哈夫曼树构造的过程：

首先统计每个字母在字符串里出现的频率，我们把每个字母看成一个结点，结点的权值即是字母出现的频率，我们把每个结点看成一棵只有根结点的二叉树，一开始把所有二叉树都放在一个集合里。接下来开始如下编码：

步骤一：从集合里取出两个根结点权值最小的树 a 和 b，构造出一棵新的二叉树 c，二叉树 c 的根结点的权值为 a 和 b 的根结点权值和，二叉树 c 的左右子树分别是 a 和 b。

步骤二：将二叉树 a 和 b 从集合里删除，把二叉树 c 加入集合里。

重复以上两个步骤，直到集合里只剩下一棵二叉树，最后剩下的就是哈夫曼树了。

我们规定每个有孩子结点的结点，到左孩子结点的路径为 0，到右孩子结点的路径为 1。每个字母的编码就是根结点到字母对应结点的路径。

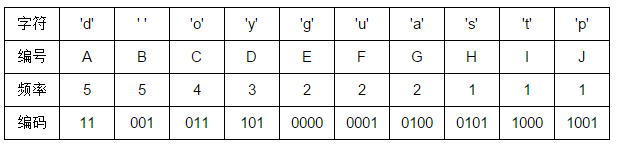
3.实例模拟哈夫曼树的构造：

例如有这一个字符串“good good study day day up”，现在我们要对字符串进行哈夫曼编码，该字符串一共有 26 个字符，10 种字符，我们首先统计出每个字符的频率，然后按从大到小顺序排列如下（第二列的字符是空格）：

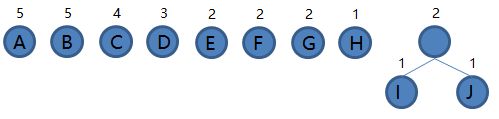
我们把每个字符看成一个结点，权值是字符的频率，每个字符开始都是一棵只有根结点的二叉树，如下图。

1.从集合里取出根结点权值最小的两棵树 I 和 J 组成新的二叉树 IJ，根结点权值为 1 + 1 = 2，将二叉树 IJ 加入集合，把 I 和 J 从集合里删除，如下图。

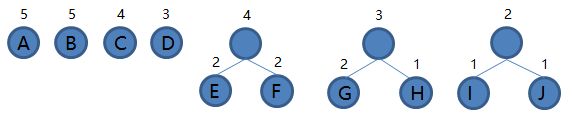
2.从集合里取出根结点权值最小的两棵树 H 和 G 组成新的二叉树 HG，根结点权值为 1 + 2 = 3，将二叉树 HG 加入集合，把 H 和 G 从集合里删除，如下图。

3.从集合里取出根结点权值最小的两棵树 E 和 F 组成新的二叉树 EF，根结点权值为 2 + 2 = 4，将二叉树 EF 加入集合，把 E 和 F 从集合里删除，如下图。

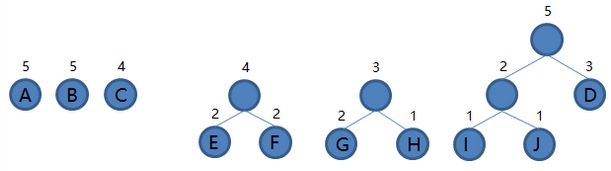
4.从集合里取出根结点权值最小的两棵树 IJ 和 D 组成新的二叉树 IJD，根结点权值为 2 + 3 = 5，将二叉树 IJD 加入集合，把 IJ 和 D 从集合里删除，如下图。

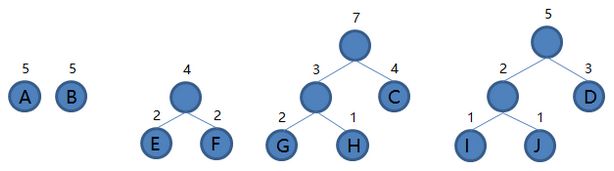
5.从集合里取出根结点权值最小的两棵树 GH 和 C 组成新的二叉树 GHC，根结点权值为 3 + 4 = 7，将二叉树 GHC 加入集合，把 GH 和 C 从集合里删除，如下图。

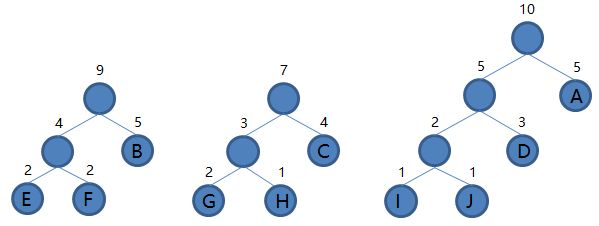
6.从集合里取出根结点权值最小的两棵树 EF 和 B 组成新的二叉树 EFB，根结点权值为 4 + 5 = 9，将二叉树 EFB 加入集合，把 EF 和 B 从集合里删除，如下图。

7.从集合里取出根结点权值最小的两棵树 IJD 和 A 组成新的二叉树 IJDA，根结点权值为 5 + 5 = 10，将二叉树 IJDA 加入集合，把 IJD 和 A 从集合里删除，如下图。

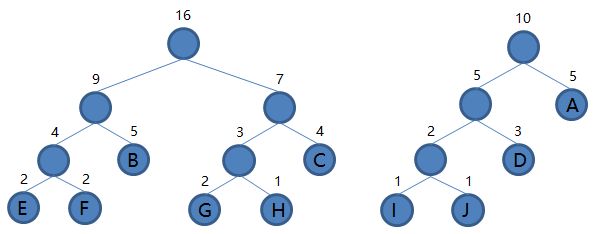
8.从集合里取出根结点权值最小的两棵树 EFB 和 GHC 组成新的二叉树 EFBGHC，根结点权值为 9 + 7 = 16，将二叉树 EFBGHC 加入集合，把 EFB 和 GHC 从集合里删除，如下图。

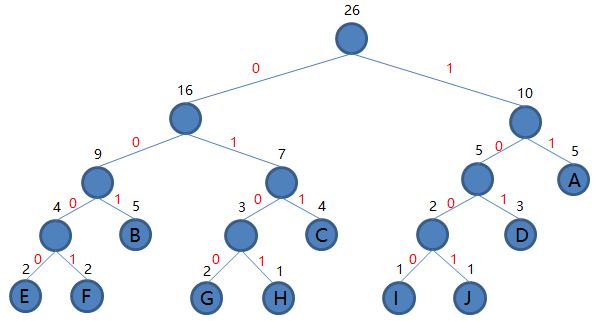
9.从集合里取出根结点权值最小的两棵树 EFBGHC 和 IJDA 组成新的二叉树 EFBGHCIJDA，根结点权值为 16 + 10 = 26，将二叉树 EFBGHCIJDA 加入集合，把 EFBGHC 和 IJDA 从集合里删除，如下图。

到这里我们发现集合里就剩一棵二叉树了，那么编码结束，最后这棵二叉树就是我们要得到的哈夫曼树。接下来我们规定非叶子结点的结点，到左子树的路径记为 0，到右子树的路径记为 1，如下图：

根结点到每个叶子结点的路径便是其对应字母的编码了，于是我们可以得到：

下面我们来算一下哈夫曼树的带权路径长度 WPL，也就是每个叶子到根的距离乘以叶子权值结果之和。

WPL = 5 * 2 + 5 * 3 + 4 * 3 + 3 * 3 + 2 * 4 + 2 * 4 + 2 * 4 + 1 * 4 + 1 * 4 + 1 * 4 = 82。

我们来算下如果直接存储字符串需要多少个比特，我们知道一个字符占一个字节，一个字节占 8 个比特，所以一共需要 8 * 26 = 208 个比特。我们再来看看哈夫曼编码需要多少个比特，我们可以发现 WPL 也就是编码后原来字符串所占的比特总长度 82。显然，哈夫曼编码把原数据压缩了好多，而且没有损失。

根据上面的实例分析，我们得出哈夫曼编码的一些性质：

1.在哈夫曼树上，相对来说，权值大的结点离根结点近，权值小的结点离根结点远

2.哈夫曼编码每次从集合里取出根结点权值最小的两棵二叉数构成新的二叉树

3.哈夫曼树的 WPL（树的带权路径长度），等于编码后字符串所占的比特数

4.哈夫曼树上不会存在只有一个孩子结点的结点

未完待续....