【算法】B+树的研读及实现（1）

【前言】

为什么要明白b+树？假如大家有操作数据库及开发有关数据库的经验，那么肯定知道索引这个概念，那么进一步问你什么叫索引？

mysql的索引就是B+树，而其他数据库我不太清楚，但是，b+树是一般的索引算法，当然，oracle、postgres等数据库听说也支持r树的索引方式。

本篇文章先说说b+树及相应实现方式。

有兴趣的话请参阅一下系列文章：

MySQL索引背后的数据结构及算法原理

假如大家对b+树的操作还不是很清楚的话，那么可以查看下面这一步操作，不过，假如您已经实现了b树，那么b+树肯定不会难倒您了。

图解B+树的插入和删除(一看就懂）点击打开

备注：

请注意两件事，第一：b+树的非叶子节点不包含任何数据，只包含数据关键字的边界，所以，叶子节点里面的关键字包含非叶子节点的关键字，假如碰到非叶子节点拥有叶子节点没有的关键字，请看看这棵树是不是b+树；

第二：非叶子节点的第一个关键字可以是上边界，也可以是下边界，关键看你如何处理这个算法。

现在补充一些b+树的定义及规则：

(1) 每个节点最多可以有m个元素；

(2) 除了根节点外，每个节点最少有 (m/2) 个元素；

(3) 如果根节点不是叶节点，那么它最少有2个孩子节点；

(4) 所有的叶子节点都在同一层；

(5) 一个有k个孩子节点的非叶子节点有 (k-1) 个元素，按升序排列；

(6) 某个元素的左子树中的元素都比它小，右子树的元素都大于或等于它；

(7) 非叶子节点只存放关键字和指向下一个孩子节点的索引，记录只存放在叶子节点中；

(8) 相邻的叶子节点之间用指针相连。

请注意，根节点可以是叶子节点，这种情况出现在什么地方呢？通常是你刚刚插入关键字的时候，只有1到两个关键字，没有满足分裂条件，所以刚开始插入数据要考虑这种情况了。

【经过刻苦的程序编写及调试，演示程序又完成了，其中最麻烦的部分是拓扑图的定位及b+树的插入删除操作-----bug的程序员的命运，这个程序虽然不大，但是各种状况各种测试也让人无奈，ok，下面演示一颗b+树如何插入，如何删除】

说明：这棵b+树的阶为3，则最多三个关键字，最多三个子树，最少2个关键字，最少两个子树。

【插入操作演示】

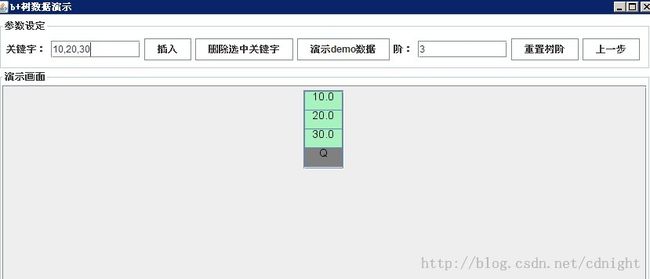
【分别插入关键字 10、20、30，此时根节点为叶节点，同时没有满足分裂条件，故放到同一个叶节点里面】

【插入关键字7，这时候根节点的关键字数量大于m（m=3），所以需要分裂成为两个子节点（叶节点）】

【分别插入关键字8、25，叶子节点被填满，没有符合分裂条件，不需要分裂。】

【插入关键字6，注意，6是少于所有关键字的，根据我的算法，6将放到最左边的叶子节点里面，并且递归设置每一个父亲的第一位数目（则该路径上第一个关键字都改6），同时，叶子节点关键字大于m（m=3），需要分裂，具体算法可以查看我的下一篇博文的具体代码，里面已经包含解释】

【分别插入关键字 7.5、12】

【插入关键字13，叶子节点满足分裂条件，分裂以后递归调整b+树的形状】

【插入关键字6.5，满足分裂条件，分裂之。】

【下面进行删除操作演示】

【删除关键字12.0，删除后叶子节点关键字数量少于min（min=2），通过检查可知，右侧兄弟有多余的关键字，从右侧兄弟那里借一个关键字，具体算法可以参看我下一篇博文的代码，里面有注释。】

【删除关键字13.0，删除后关键字数量少于min，并且左右兄弟都没有多余的关键字，所以只能够合并叶子节点，合并后需要递归进行树形结构调整，具体算法参看下一篇博文。】

【删除关键字7.5，删除后满足合并条件，进行合并并递归调整树形。】

【删除关键字6.0，删除关键字6.0后，关键字数量==min，符合树形结构，但是父节点的关键字代表的是界限，就本算法而言，父亲节点的关键字要大于或等于它对应子节点或叶子节点的所有关键字，所以，这里必须进行父亲节点下界关键字的调整，必要时（当最左边叶子节点的第一个关键字改变了的情况下）甚至需要将同一路径的所有第一个关键字都改变，具体算法参看下一篇博文。】

【删除关键字8.0，删除后需要向右边兄弟借一个关键字。】

【删除关键字10.0，需要合并。】

好了，想必大家对b+树的添加及删除操作有所认识了，下面我将演示用程序放出来，

b+树演示工具