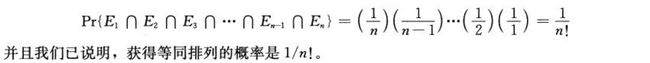第五章 概率分析和随机算法
5.1 雇佣问题
雇佣问题类似于在一组随机排序的数组中查询最大值的问题,对于这类问题无法确切的得出其运行效率。但可以根据输入的概率分布得到平均情况运行时间。对于一个算法行为不仅由输入决定,而且由随机数生成器产生的数值决定,则称算法是随机的,其运行时间称为期望运行时间。
5.2指示器随机变量
由指示器随机变量计算雇佣问题的期望
5.3 随机算法
对于一个输入为随机的问题只可以讨论平均情况运行时间,若欲讨论其期望运行时间,则可以使用随机算法将输入进行随机排列。
将一个输入转化为一个随机排列数组,使得产生的排列个数是N!个,且每种排列的概率相同,即都为1/N!,采用两种方法:
import random
def MERGE(A, B, p, q, r):
L = A[p:q]
LB = B[p:q]
L.append(float("inf"))
R = A[q:r]
RB = B[q:r]
R.append(float("inf"))
i = 0
j = 0
for k in range(p, r):
if L[i] <= R[j]:
B[k] = LB[i]
A[k] = L[i]
i = i + 1
else:
B[k] = RB[j]
A[k] = R[j]
j = j + 1
def MERGE_SORT(A, B, p, r):
if p < r-1:
q = (p + r) // 2
MERGE_SORT(A, B, p, q)
MERGE_SORT(A, B, q, r)
MERGE(A, B, p, q, r)
def PERMUTE_BY_SORTING(A):
n = len(A)
P = []
for i in range(0, n):
p = random.randint(0, n ** 3)
P.append(p)
MERGE_SORT(P, A, 0, n)
def RANDOMIZE_IN_PLACE(A):
n = len(A)
for i in range(0, n):
randIndex = random.randint(i, n-1)
temp = A[i]
A[i] = A[randIndex]
A[randIndex] = temp

5.4 概率分析和指示器随机变量的进一步使用
生日悖论:n个人中,两个人生日落在第i天的概率为1/(n^2),则两人同一天生日的概率为其期望,值从第一天到第n天有n*(1/(n^2)) = 1/n。至少有两个人在同一天生日的概率大于1/2,即为不存在同一天生日的排列的补集(1 - p)大于1/2, 则p小于1/2,若采用随机变量指示器计算其期望C(k, 2)*(1/n)
球与箱子:投球符合几何分布,第i-1次命中到第i次命中之间的投球次数的期望为1/((b-i+1)/b) = b/(b-i+1),则每个箱子中至少有一个球的期望为1到b的和为b(ln(b) + O(1))。
特征序列:共n次实验,连续出现k次正面向上的期望值为X(k),每种可能的概率为从i到i+k < n出现正面向上的概率,i的值从1到n-k+1,连续出现k次的概率为1/(2^k),则期望x为这些概率的和 = (n - k + 1)/(2^k),特征序列即:使得期望达到最大时k的值,转化为求最大值问题,当k = lg(n) 时最大。
在线雇佣问题:面试n个人,抛弃前k个人,雇佣k+1到n中第一个比之前都优秀的人其位置为i。在位置i雇佣到最佳人选的期望值X(k),每一个可能的i为k+1到n,最佳人选在位置i被雇佣的概率由最佳人选排在位置i概率为1/n,且k+1到i-1之间不会有人被聘用即其中的最大值只在1到k之间概率为k/(i-1)。两个概率之积,并由k+1到n的和的期望达到最大值时k的值即为问题的解。
习题解答