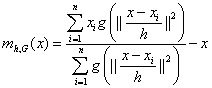MeanShift算法(一)
参考论文:D. Comaniciu and P. Meer, “Mean shift: A robust approach toward feature space analysis,” IEEE T. PAMI, vol. 24, no. 5, pp. 603-619, May 2002
MeanShift 可以翻译为“均值漂移”,它在聚类、图像平滑、图像分割和跟踪方面得到了比较广泛的应用。MeanShift 这个概念最早是由Fukunaga等人于1975年在一篇关于概率密度梯度函数的估计(The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition)中提出来的。其最初含义正如其名:就是偏移的均值向量。在这里MeanShift是一个名词,它指代的是一个向量。但随着Mean Shift理论的发展,MeanShift的含义也发生了变化。如果我们说MeanShift算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点到其偏移均值,然后以此为新的起始点继续移动,直到满足一定的条件结束。
在很长一段时间内,MeanShift算法都没有得到足够的重视,直到1995年另一篇重要论文的发表。该论文的作者Yizong Cheng定义了一族核函数,使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。其次,他还设定了一个权重系数,使得不同样本点的重要性不一样,这大大扩展了MeanShift的应用范围。此外,还有研究人员将非刚体的跟踪问题近似为一个MeanShift的最优化问题,使得跟踪可以实时进行。目前,利用MeanShift进行跟踪已经相当成熟。MeanShift算法其实是一种核密度估计算法,它将每个点移动到密度函数的局部极大值点处。
下面介绍MeanShift算法的理论:
在给定d维空间Rd的n个样本点![]() ,i=1,…,n.则核密度估计函数可以表示为:
,i=1,…,n.则核密度估计函数可以表示为:
核函数K(x)满足如下关系:
归一化:
对称性:
权重的指数衰减:
?????条件:
其中上式c为常数。对于有限数量的data,实际应用中K(x)有两种获取的形式:
![]()
第一种形式,在各个维度上都使用相同的函数k(x),第二种形式表示只使用了向量的长度。因为||*||表示欧式距离。在Rd表示的d维空间中,参数h是样本数量n的函数,应当满足![]() ,从而保证估计的渐进无偏性。为了确保估计的均方一致性,h需要满足条件:。为了确保全局一致性,h需要满足条件
,从而保证估计的渐进无偏性。为了确保估计的均方一致性,h需要满足条件:。为了确保全局一致性,h需要满足条件![]() .
.
其中,当核函数采用Epanechnikov核时,均方误差最小。Epanechnikov核表示为:
其中![]() 为d维单位球体体积。另外一个也被用到的核函数为高斯核:
为d维单位球体体积。另外一个也被用到的核函数为高斯核:
定义核函数的轮廓(profile,也可翻译为剖面函数)函数k(x)满足k:[0,![]() )->R,即
)->R,即
![]()
其中为归一化常数,保证K(x)积分为1,且严格为正。由此带入最初的核密度估计函数,可将核密度估计函数重写为:
下面介绍Kernel DensityGradient Estimation:
定义一个轮廓函数(profile)![]() ,并且构造出g(x)的核函数:
,并且构造出g(x)的核函数:
![]()
参考文献中说K(x)was called the shadow of G(x),这里不太理解这个shadow的意思?同样也说Epanechnikov kernel is the shadow of the uniform kernel??
根据核函数的可微性,密度梯度估计恒等于核密度估计的梯度,可以得到:
将g(x)带入上式得到:
假设大于0。可以得到关于核函数G在点x的表达式如下,可理解为以G为核函数对概率密度函数f(x)的估计:
则mean shift向量可表示为:
以核函数作为权重,x作为窗口的中心。
上面的式子表明,在点x处,基于核函数G(x)的mean shift向量与基于核函数K(x)的密度梯度估计仅相差一个常数的比例系数。而梯度是指密度变化最大的方向,所以mean shift向量也是指向密度增大最大的方向。
反复进行以下步骤就是MeanShift算法的过程:
1)计算mean shift向量![]() ;
;
2)根据![]() ,移动核(窗口);
,移动核(窗口);
3)若,则结束循环,否则继续迭代。
最终核函数的中心点收敛到数据空间中密度最大的点,它的密度梯度估计为0。mean shift向量也总是指向密度增大最大的方向,这可由上式的分子项来保证。而分母项则表示每次迭代核函数移动的步长。在不包含兴趣特征的区域内,步长较长;在感兴趣的区域内,步长较短。即MeanShift算法是一个变步长的梯度上升算法,或称为自适应梯度上升算法。
小结:
根据mean shift向量,定义半径为h的高维球区域Sh,并满足一下关系的y点的集合:
k表示在这n个点xi中,有k个点落入Sh区域中。
我们可以看到(xi - x)是样本点xi相对于点x的偏移向量。mean shift向量就是对落入区Sh中的k个样本点相对于点x的偏移向量求和然后再平均。从直观上看,如果样本点xi从一个概率密度函数f(x)中采样得到,由于非零的概率密度梯度指向概率密度增加最大的方向。因此从平均上来说,区域内的样本点更多的落在沿着概率密度梯度的方向。因此,对应的mean shift向量应该指向概率密度梯度的方向。如下图所示:
大圆圈所圈定的范围就是Sh,小圆圈代表落入Sh区域内的样本点。黑点就是meanshift的基准点,箭头表示样本点相对于基准点x的偏移向量。很明显的,我们可以看出平均的偏移向量![]() 会指向样本分布最多的区域,也就是概率密度函数的梯度方向。把每个偏移向量相加就可以得到meanshift向量,再以meanshift向量的终点,即质心画球,移动,重复此过程即可收敛到概率密度最大的方向。即最稠密,密集的地方。
会指向样本分布最多的区域,也就是概率密度函数的梯度方向。把每个偏移向量相加就可以得到meanshift向量,再以meanshift向量的终点,即质心画球,移动,重复此过程即可收敛到概率密度最大的方向。即最稠密,密集的地方。