图像处理中两种基本的插值算法(最邻近插值法和双线性内插法)

在图像的基本仿射变换中，经常会碰到经过旋转、缩放后灰度值如何赋值的问题。因为变换之后，图像的坐标位置有可能是小数，所以就需要插值算法来确定到底将该像素赋予哪个位置。

1、最邻近插值法(Nearest Interpolation)

这是最简单的一种插值方法，不需要计算。在待求像素的四邻像素中，将距离待求像素最近的邻接像素灰度值赋予待求像素。设i+u, j+v(i, j为正整数， u, v为大于零小于1的小数，下同)为待求象素坐标，则待求象素灰度的值 f(i+u, j+v) 如下图所示：

如果(i+u, j+v)落在A区，即u<0.5, v<0.5，则将左上角象素的灰度值赋给待求象素，同理，落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。

最邻近元法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。

2、双线性内插法(Bilinear Interpolation)

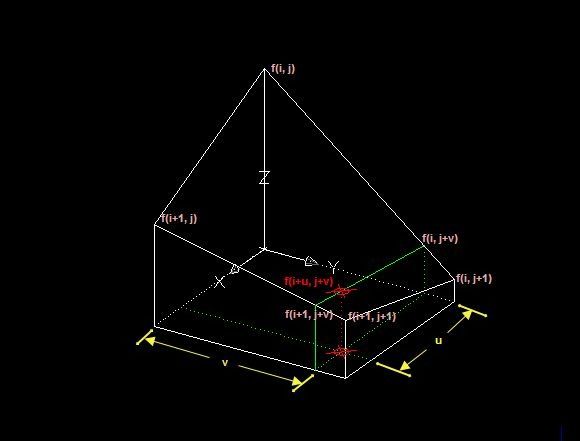
双线性内插法是利用待求象素四个邻象素的灰度在两个方向上作线性内插，如下图所示：

对于 (i, j+v)，f(i, j) 到 f(i, j+1) 的灰度变化为线性关系，则有：

f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)

同理对于 (i+1, j+v) 则有：

f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)

从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系，由此可推导出待求象素灰度的计算式如下：

f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)

双线性内插法的计算比最邻近点法复杂，计算量较大，但没有灰度不连续的缺点。它具有低通滤波性质，使高频分量受损，图像轮廓可能会有一点模糊。图像看起来更光滑。

以上文章转自http://www.cnblogs.com/linzhao/archive/2012/02/16/2354175.html

下面贴上主要实验代码：

//nearest interpolation method for resize(zoom)
void onNearest(CDib &m_Dib, BYTE **srcImg,BYTE **dstImg,int h,int w,double zoomNumber)
{
	int ey,ex;
	int j,i;
	int zoomH = (int)(zoomNumber*h + 0.5);
	int zoomW = (int)(zoomNumber*w + 0.5);
	int originalLineByte = ((w % 4 == 0 ? w : w + (4 - (w % 4)))*m_Dib.GetBitCount())/8; //align the width
	int zoomLineByte = ((zoomW % 4 == 0 ? zoomW : zoomW + (4 - (zoomW % 4)))*m_Dib.GetBitCount())/8;
	BYTE *temp = new BYTE[w * h];
	for(j=0;j<h;j++) //copy original image to the buffer
	{
		for(i=0;i<w;i++)
		{
			temp[j*w+i] = srcImg[j][i];  
		}
	}
	BYTE *newImg = new BYTE [zoomLineByte * zoomH];
	for(ey = 0;ey < zoomH;ey++)
	{
		for(ex = 0; ex < zoomLineByte;ex++)
		{
			j = (int)(ey/zoomNumber + 0.5); //nearest value
			i = (int)(ex/zoomNumber + 0.5);
			if((i >= 0) && (i < w) && (j >= 0)&& (j < h))
			{	
				 //memcpy(&newImg[ey * zoomLineByte] + ex * m_Dib.GetBitCount() / 8,&temp[j * originalLineByte] + i * m_Dib.GetBitCount() <span style="white-space:pre">				</span> //<span style="white-space:pre">			</span>/ 8,m_Dib.GetBitCount() / 8); 			
				newImg[ey*zoomLineByte+ex] = temp[j*originalLineByte+i];
			}
			else
			{
				newImg[ey*zoomLineByte+ex] = 255;
			}
			dstImg[ey][ex]=newImg[ey*zoomLineByte+ex];
		}
	}
}

//bilinear interpolation method for resize(zoom)
void onBilinear(CDib &m_Dib,BYTE **srcImg,BYTE **dstImg,int h, int w,double zoomNumber)
{
	int ey,ex;
	int j,i;
	int zoomH = (int)(zoomNumber*h + 0.5);
	int zoomW = (int)(zoomNumber*w + 0.5);
	int originalLineByte = ((w % 4 == 0 ? w : w + (4 - (w % 4)))*m_Dib.GetBitCount())/8; //align the width
	int zoomLineByte = ((zoomW % 4 == 0 ? zoomW : zoomW + (4 - (zoomW % 4)))*m_Dib.GetBitCount())/8;
	BYTE *temp = new BYTE[w * h];

	for(j=0;j<h;j++) //copy original image to the buffer
	{
		for(i=0;i<w;i++)
		{
			temp[j*w+i] = srcImg[j][i];  
		}
	}

	BYTE *newImg = new BYTE [zoomLineByte * zoomH];

	for(ey = 0;ey < zoomH;ey++)
	{
		for(ex = 0;ex < zoomLineByte;ex++)
		{
			double jz = ((double)ey)/zoomNumber;  //get the original image coordinates
			double iz = ((double)ex)/zoomNumber;
			int j1 = (int)jz;
			int i1 = (int)iz;
			int j2 = j1 + 1;
			int i2 = i1 + 1;
			double u = iz - i1;					//插值点与邻近整数点(j1,i1)的距离 x coordinate
			double v = jz - j1;					// y coordinate

			double s1 = (1.0 - u)*(1.0 - v);		<span style="white-space:pre">	</span>//邻近整数点(j1,i1)函数值的系数（左上角）left-up corner
			double s2 = (1.0-u)*v;				<span style="white-space:pre">	</span>//邻近整数点(j1,i1)函数值的系数（左下角）left-down corner
			double s3 = u*(1.0 - v);				//邻近整数点(j1,i1)函数值的系数（右上角）right-up corner
			double s4 = u*v;					//邻近整数点(j1,i1)函数值的系数（右下角）right-down corner

			if((jz >=0) && (jz < h) && (iz >= 0) && (iz < w))
			{
				*(newImg+ey*zoomLineByte+ex) = *(temp+j1*originalLineByte+i1)*s1
					+*(temp+j1*originalLineByte+i2)*s3
					+*(temp+j2*originalLineByte+i1)*s2
					+*(temp+j2*originalLineByte+i2)*s4;
				}
				else
				{
					*(newImg+ey*zoomLineByte+ex) = 255;
				}
			dstImg[ey][ex]=newImg[ey*zoomLineByte+ex];
		}
	}
}

实验效果如下图所示：分别放大了1.5倍

最邻近插值：

双线性内插：

可以看到最邻近插值图像中有明显的锯齿状，而双线性内插结果图中比较光滑，也带一点模糊的感觉。

其他参考链接：

http://zh.wikipedia.org/wiki/%E5%8F%8C%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC

http://en.wikipedia.org/wiki/Bilinear_interpolation