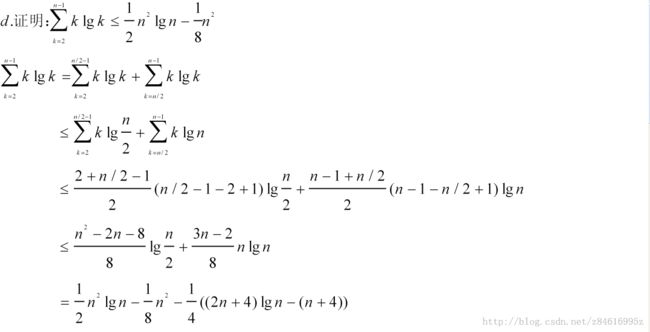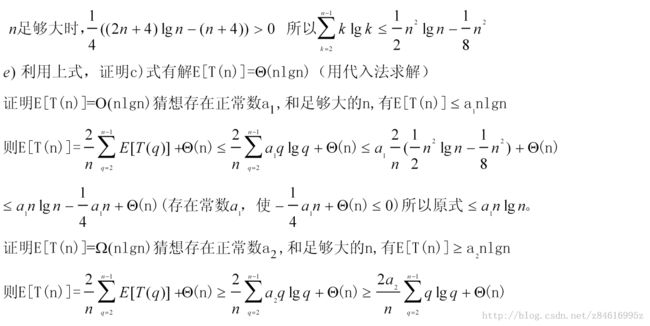算法导论第七章最后思考题

7-1（Hoare划分的正确性） 本章中的PARTITION算法并不是其最初版本。下面给出的是最早由C.R.Hoare所设计的划分算法：

HOARE-PARTITION(A,p,r)

1. x=A[p]

2. i=p-1

3. j=r+1

4. while TRUE

5.         repeat

6.                j=j-1

7.         until A[j]<=x

8.         repeat

9.                i=i+1

10.       until A[j]>=x

11.       if i<j

12.           exchange A[i] with A[j]

13.       else return j

a. 试说明 HOARE-PARTITION 在数组A={13,19,9,5,12,8,7,4,11,2,6,21}上的操作过程，并说明在每一次执行4-13行while循环时数组元素的值和辅助变量的值。后续的三个问题要求

读者仔细论证HOARE-PARTITION 的正确性。在这里假设子数组A[p..r]至少包含来2个元素，试证明下列问题。

a)X=13作为主元。

 A={13,19,9,5,12,8,7,4,11,2,6,21} 第一次大循环后A[i=0]=13与A[j=10]=6交换

 A={6,19,9,5,12,8,7,4,11,2,13,21} 第二次大循环后A[i=1]=19与A[j=9]=2交换

 A={6,2,9,5,12,8,7,4,11,19,13,21} 第三次循环后(i=9)>(j=8) 函数返回j j以前的数[0,8](包括j)比i以后的数[9,11](包括i)小

这样完成了一次以X=13作为主元的划分。

b. 下标i和j可以使我们不会访问在子数组A[p..r]以外的数组A的元素。

i初始=p-1 并且是递增的，所以i>=p-1。而j初始=r+1 并且是递减的,所以j<=r+1。外层循环运行的条件是p-1<=i<j<=r+1.所以i递增不会大于r,而j递减不会小于p,又因为当i>j时，程序终止。i和j比较作为外层循环与否的条件限制了子数组的访问。

c.当HOARE-PARTITION结束时，它返回的值j 满足p<=j<r。

第一个内层循环，j--最多减少到p,因为A[p]=x，所以第一个内层循环不得不终止，所以p<=j.
第一个内层循环，j--如果只循环了一次就终止，那么有A[r]=x,所以A[p]=A[r]=x 所以子数组内只有一个元素，这与题目
假设不符，所以第一个内层循环要循环2次，j=r-1<r 所以p<=j<r

d.当HOARE-PARTITION结束时，A[p..r]中的每一个元素都小于或等于A[j+1..r]中的元素。

第一个内层循环的作用是找到数组右半部分小于主元的位置j.第二个内层循环的作用是找到数组左半部分大于主元的位置i
然后位置j的元素A[j]和位置i的元素A[i]互换，这样循环数次后，左半部分都小于主元，右半部分都大于主元，完成了划分。

      在7.1节的PARTITION过程中，主元(原来存储在A[r]中)是与它划分的两个分区分离的。与之对应，在HOARE-PARTITION中，主元(原来存储在A[p]中)是存在与分区A[p..r]与A[j+1..r]中的。因为有p<=j<r，所以这一划分总是平凡的。

e).利用HOARE-PARTITION，重写QUICKSORT算法。//C++中的do-while循环相当于伪代码的repeat-until循环。于是就有下面的代码。

#include <iostream>
using namespace std;
int PARTITION(int A[],int p,int r)
{
    int x=A[p];
    int i=p-1;
    int j=r+1;
    while (1)
    {
        do 
        {
           j--;
        } while (A[j]>x);
        do 
        {
           i++;
        } while (A[i]<x);
        if (i<j)
        {
            swap(A[i],A[j]);
        }
        else return j;
    }
}
void QUICKSORT(int A[],int p,int r)
{
    if (p<r)
    {
        int q=PARTITION(A,p,r);
        QUICKSORT(A,p,q);
        QUICKSORT(A,q+1,r);
    }
}
void main()
{
    int A[16]={1,5,10,8,9,4,6,2,7,3,20,21,11,15,29,14};
    QUICKSORT(A,0,15);//K=3
    for (int i=0;i<16;i++)
    {
        cout<<A[i]<<" ";
    }
    cout<<endl;
}

7-2（针对相同元素值得快速排序）在7.4.2节对随机化快速排序的分析中，我们假设输入元素的值是互异的，在本题中，我们将看看如果这一假设不成立会出现什么情况？

//本题是替换掉了第二版的7-2，属于第三本的新题。所以网上答案也比较少见。故经过我深思熟虑(通篇全部原创),想出了和第三版《教师手册》不太一样的答案。

a) 如果所有输入元素的值都相同，那么随机化快速排序的运行时间会是多少？

如果所有输入元素的值都相同，那么每次划分都是极不平衡的。每次都是T(n)=T(0)+T(n-1)+Θ(n)   T(n)=Θ(n^2)

b).PARTITION过程返回一个数组下标q,使得A[p..q-1]中的每个元素都小于等于A[q]，而A[q+1..r]中的每个元素都大于A[q]。修改PARTITION代码来构造一个新的PARTITION‘(A,p,r)

，它排列A[p..r]的元素，返回值是两个数组下标q和t,其中p<=q<=t<=r，且有

    A[q..t]中的所有元素都相等。

    A[p..q-1]中的每个元素都小于A[q]。

    A[t+1..r]]中的每个元素都大于A[q]。

与PARTITION类似，新构造的PARTITION’的时间复杂度是Θ(r-p)。

#include <iostream>
#include <time.h>
using namespace std;
int PARTITION(int A[],int p,int r)
{
    int x=A[r];
    int i=p-1,k=0,t=r;
    for (int j=p;j<r-1;j++)//循环了r-1-p+1次=r-p次
    {//此循环的目的是将所有和主元相同的元素都移动到数组最右边
        if(A[j]==x)
        {
             if(A[j]!=A[r-1])
             {
               swap(A[j],A[r-1]);
               r--;
             }
             else 
             {
               j--;r--;
             }
        }       
    }
    for (j=p;j<=r-1;j++)//循环了r-1-p+1次=r-p次
    {//此循环的目的是记录第一个大于主元的元素A[i]
        if (A[j]<=x)
        {
            i++;
            swap(A[i],A[j]);
        }
    }
    for (int h=0;h<t-r+1;h++)//循环了t-r+1-0=t-r+1次,这也正是数组中相同元素个数，相同元素个数<=r-p
    {//此循环的目的是将已经划分好的数组的最右边和主元相同的元素移动到大于主元和小于主元之间。
        swap(A[i+h+1],A[r+h]);
    }
    return i+1;
}
//经过这三个循环 有T(n)=O(r-p)+O(r-p)+O(t-r+1)=O(r-p)
void main()
{
    //int A[16]={1,5,8,2,9,5,5,7,6,16,10,15,12,4,5,5};
    //int A[16]={1,5,10,3,3,4,3,3,7,3,20,21,11,15,3,3};
    //PARTITION(A,0,15);//K=3
    //for (int i=0;i<16;i++)
    //{
       // cout<<A[i]<<" ";
    //}
    //cout<<endl;
    int A[100]={0};
    srand( (unsigned)time( NULL ) );
    for (int i=0;i<100;i++)
    {
        A[i]=rand()%(100-50+1)+50;
    }
    cout<<"快速排序前的随机数组："<<"其中主元:"<<A[99]<<endl;
    for ( i=0;i<100;i++)
    {
        cout<<A[i]<<" ";
    }
    cout<<endl;
    //QUICKSORT(A,0,15);//K=3
    int x=PARTITION(A,0,99);
    cout<<"主元前面的数为:"<<endl;
    for ( i=0;i<x;i++)
    {
        cout<<A[i]<<" ";
    }
    cout<<endl;
    cout<<"主元后面的数为:"<<endl;
    for ( i=x;i<100;i++)
    {
        if (A[x]!=A[i])
        {
            cout<<A[i]<<" ";
        }
    }
    cout<<endl;
}

c.将RANDOMIZED-QUICKSORT过程改为调用PARTITION',并重新命名为RANDOMIZED-QUICKSORT‘。修改QUICKSORT的代码构造一个新的QUICKSORT’(A,p,r),它调用RANDOMIZED-QUICKSORT‘，并且只有分区内的元素互异时候才做递归调用。

#include <iostream>
#include <time.h> 
using namespace std;
int PARTITION(int A[],int p,int r,int &k)
{//这个方法涉及到了三个循环，但是每个循环的时间复杂度都不超过O(n)，所以总的时间复杂度是符合题意的。只不过时间复杂度的常数项稍大一些。
    int x=A[r];
    int i=p-1,t=r;
    for (int j=p;j<r-1;j++)//循环了r-1-p+1次=r-p次
    {//此循环的目的是将所有和主元相同的元素都移动到数组最右边
        if(A[j]==x)
        {
            if(A[j]!=A[r-1])//判断A[j]与挨着主元左边的那个元素是否相等
            {
                swap(A[j],A[r-1]);//不等。就交换，目的是把等于主元的A[j]移动到最右边
                r--;
            }
            else //相等。就减少r的上限值，直到A[r-1]与A[j]不等。
            {
                j--;r--;//j--，只要A[r-1]与A[j]相等，j值经过循环就不变位置，直到两者不等。
            }
        }       
    }//整个循环结束后，所有和当前主元相同的元素都移动到了数组右边
    for (j=p;j<=r-1;j++)//循环了r-1-p+1次=r-p次
    {//此循环的目的是记录第一个大于主元的元素A[i]
        if (A[j]<x)
        {
            i++;
            swap(A[i],A[j]);
        }
    }
    for (int h=0;h<t-r+1;h++)//循环了t-r+1-0=t-r+1次,这也正是数组中相同元素个数，相同元素个数<=r-p
    {//此循环的目的是将已经划分好的数组的最右边和主元相同的元素移动到大于主元和小于主元之间。
        swap(A[i+h+1],A[r+h]);
    }
    k=t-r+1;//计算和主元相同的元素个数
    return i+1;
}
int RANDOMIZED_PARTITION(int A[],int p,int r)
{
    srand( (unsigned)time( NULL ) );
    int i=rand()%(r-p+1)+p,k=0;
    swap(A[r],A[i]);
    return PARTITION(A,p,r,k);
}
void QUICKSORT(int A[],int p,int r)
{
    int k=0;
    if (p<r)//T(n)=2
    {
        int q=PARTITION(A,p,r,k);//q为主元起始位置，k表示相同主元的个数。
        int t=q+k-1;//t为和主元相同的元素最后一位，所以[q,t]之间内的元素相同
        QUICKSORT(A,p,q-1);//[p,q-1]与[t+1,r]内的元素互不相同
        QUICKSORT(A,t+1,r);
    }
}
void main()
{
    
    int A[100]={0};
    srand( (unsigned)time( NULL ) );
    for (int i=0;i<100;i++)
    {
        A[i]=rand()%(100-50+1)+50;
    }
    QUICKSORT(A,0,99);
    for ( i=0;i<100;i++)
    {
        cout<<A[i]<<" ";
    }
    cout<<endl;
}

以上程序是我自己写的。。实现的和《教师手册》答案有些不同，我这个是由三个循环组成的。所以T(n)=T(q-1)+T(n-q-1)+Θ(n)中的Θ(n)所含常数项稍微大了些，而《教师手册》答案虽然很简短而高效，只用了一个循环就OK了，Θ(n)项含的常数也比较小，但是我没看明白。

d.在QUICKSORT‘中,应该如何改变7.4.2节中的分析方法，从而避免所有元素都是互异的这一假设？

这个还是由高手回答吧。。想半天也没想出来。。

7-3(另一种快速排序的分析方法) 对随机化版本的快速排序算法，还有另一种性能分析方法，这一方法关注与每一次单独递归调用的期望运行时间，而不是比较的次数。

a.证明：给定一个大小为n的数组，任何特定元素被选为主元的概率为1/n。利用这一点来定义指示器随机变量Xi=I{第i小的元素被选为主元}，E[Xi]是什么？

第i小元素被选为主元的概率为1/n,根据引理5.1 E(Xi)=1/n.

b.设T(n)是一个表示快速排序在一个大小为n的数组上的运行时间的随机变量，试证明：E[T(n)]=E[∑Xq(T(q-1)+T(n-q)+Θ(n))]

Xq为第q个元素划分的概率，E(Xq)=Xq第q个元素划分的时间复杂度是Tq=T(q-1)+T(n-q)+Θ(n) 这样的划分一共有n种.所以总的T(n)的时间期望值E(T(n))=X1T1+X2T2+...XqTq+...+XnTn= ∑XqTq=∑E(Xq)(T(q-1)+T(n-q)+Θ(n))=E(∑Xq(T(q-1)+T(n-q)+Θ(n)))

c.证明公式(7.5)可以改为:E[T(n)]=(2/n)∑E[(Xq)]+Θ(n)

由E[T(n)]=E[∑Xq(T(q-1)+T(n-q)+Θ(n))]知：

∑T(q-1)=T(0)+T(1)+...+T(n-1)....(1) 
∑T(n-q)=T(n-1)+T(n-2)+..+T(0) ....(2)
∑T(q)=T(0)+T(1)+...+T(n)..........(3) (以上∑都是从1到n)
所以(1)+(2)=2*(3):∑(T(q-1)+T(n-q))=2∑T(q). 
又因为Xq=1/n所以T(n)=∑(1/n)(T(q-1)+T(n-q)+Θ(n))=(1/n)(2∑T(q)+nΘ(n))=(2/n)∑T(q)+Θ(n) T(0)=T(1)=0
两边取期望，并且T(0)和T(1)可以忽略，所以就有c式。

7-4(快速排序的栈深度) 7.1节中的QUICKSORT算法包含了两个对其自身的递归调用。在调用PARTITION后，QUICKSORT分别递归调用了左边的子数组和右边的子数组。QUICKSORT中的第二个递归调用并不是必须的。我们可以用一个循环控制结构来代替它。这一技术成为尾递归，好的编译器都提供这以功能。考虑下面这个版本的快速排序，它模拟了尾递归情况。

TAIL-RECURSIVE-QUICKSORT(A,p,r)

1. while p<r

2. q=PARTITION(A,p,r)

3. TAIL-RECURSIVE-QUICKSORT(a,p,q-1)

4. p=q+1

a.证明：TAIL-RECURSIVE-QUICKSORT(A,1,A.length)能正确地对数组A进行排序，编译器同城使用栈来存储递归执行过程中的相关信息，包括每一次递归调用的参数等。最新

调用的信息存在栈的顶部，而第一次调用的信息存在栈的底部。当一个过程被调用时，其先关信息被压入栈中，当它结束时，其信息则被弹出。因为我们假设数组参数是用指针来知识的，所以每次过程调用只需要O(1)的栈空间。栈深度是在一次计算中会用到的栈空间的最大值。

第一次循环，PARTITION函数把p和r划分成两部分，小于A[q]的都放入到TAIL_RECURSIVE_QICKSORT(A,p,q-1)内，然后调用自身，继续选取主元，把小于A[q]又都放入到TAIL_RECURSIVE_QICKSORT(A,p,q-1)，经过多次对自身调用后，TAIL_RECURSIVE_QICKSORT的第三个参数减少到p=r,这样TAIL_RECURSIVE_QICKSORT开始返回，然后执行p=q+1,对每次的TAIL_RECURSIVE_QICKSORT调用的进行下一层循环，下一层循环PARTITION(A,q+1,r)是对于大于A[q]的区间进行再划分，这样不断的循环划分递归直到数组有序。

b.请描述一种场景，使得针对一个包含n个元素数组的TAIL-RECURISIVE-QUICKSORT的栈深度是Θ(n).

由a知，每次递归调用都把相关信息压入栈中，TAIL_RECURSIVE_QICKSORT(A,p,r)的第三个参数经过小于r-p=n次递归调用达到返回条件p=r所以对自身递归调用不超过n次。每次调用过程值需要O(1)的内存空间，所以不超过n次调用就是Θ(n)空间，所以由a知栈深度的定义，Θ(n)就为栈深度。

c.修改TAIL_RECURSIVE_QICKSORT的代码，使其最坏情况下栈深度是Θ(lgn)，并且能够保持O(nlgn)的期望时间复杂度。

这个是第三版《教师手册》给的答案。

QUICKSORT”(A, p,r)/
while p < r
// Partition and sort the small subarray first.
q = PARTITION(A, p,r)
if(q-p<r-q)
QUICKSORT"(A,p,q-1)/
p=q + 1
else QUICKSORT"(A,q+1,r)/
r=q+1

7-5(三数取中划分) 一种改进RANDOMIZED-QUICKSORT的方法是在划分时，要从子数组中更细致地选择作为主元的元素(而不是简单地随机选择)。常用的做法是三数取中法；从子数组中随机选出三个元素，取其中位数作为主元，对于这个问题的分析，我们不妨假设数组A[1..n]的元素是互异的且有n>=3，我们用A'[1..n]来表示已排好序的数组。用三数取中法选择主元x,并定义pi=Pr{x=A'[i]}