LeetCode 121, 122, 123. Best Time to Buy and Sell Stock i, ii, iii

1. 题目描述

Say you have an array for which the ith element is the price of a given stock on day i.

1. If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.
2. Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
3. Design an algorithm to find the maximum profit. You may complete at most two transactions.

2. 解题思路

这三道题目其实都是一个问题引申出来的， 只不过是约束条件不同。
1. 对于只能完成1次交易的情形， 其实很容易， 找到相应的最大， 最小值就可以了。

2. 对于可以多次交易的情形， 只要把每个上坡的利润相加就可以了

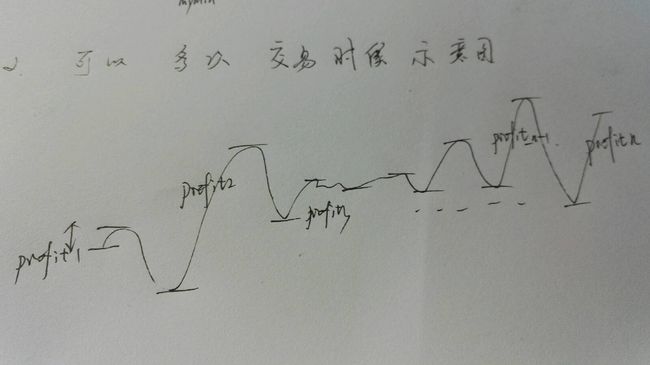
3. 而对于只能交易两次的情形， 我们可以记录下各个峰值和谷值， 采用动态规划的思想来处理这个问题，
先找出第i个上坡到第j 个上坡之间的最大利润值 ，下面给出转移方程：

然后， 在利用一次动态规划找到最大的两个区间的利润之和。（整个区间可以视为和一个空区间的结合）

3. code

3.1 code

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int sum = 0;
        int profit = 0;
        int minnum = INT_MAX;
        // 维护一个最小值， 计算每个值与最小值的 差 profit， 然后更新maxprofit
        for (int i = 0; i != prices.size(); i++){
           if (prices[i] < minnum)
                minnum = prices[i];
            profit = prices[i] - minnum;
            if (profit > sum)
                sum = profit;
        }
        return sum;
    }
};

3.2 code

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0)
            return 0;

        int profit = 0;
        int minnum = prices[0];
        int last = prices[0];
        bool incre = true;
        for (int i = 0; i != prices.size(); i++){
            // 增长阶段， 遇到顶峰 卖出
            if (incre){
                if (last > prices[i]){
                    profit += last - minnum;
                    incre = false;
                }
            } 
            // 下降阶段， 遇到谷底 买入
            else{
                if (last < prices[i]){
                    minnum = last;
                    incre = true;
                }
            }

            last = prices[i];
        }

        if (incre){
            profit += last - minnum;
        }

        return profit;
    }
};

3.3 code

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() <= 1)
            return 0;

        // 记录山峰和谷底的值
        vector<int> bot, top;
        bool incre = prices[1] - prices[0] >= 0 ? true : false;
        if (incre)
            bot.push_back(prices[0]);

        for (int i = 0; i != prices.size() - 1; i++){
            if (incre){
                if (prices[i] > prices[i + 1]){
                    incre = false;
                    top.push_back(prices[i]);
                }
            }
            else{
                if (prices[i] < prices[i + 1]){
                    bot.push_back(prices[i]);
                    incre = true;
                }
            }
        }

        if (incre)
            top.push_back(prices[prices.size() - 1]);

        // 动态规划 求每段的最大值
        vector<vector<int>> table(bot.size(), vector<int>(top.size(), 0));
        for (int i = 0; i != table.size(); i++){
            for (int j = i; j != table[0].size(); j++){
                if (j == 0)
                    table[i][j] = top[j] - bot[j];
                else
                    //table[i][j] = max(max(top[j] - bot[j], table[i][j - 1]), top[j] - bot[j] + table[i][j - 1] - (top[j - 1] - bot[j]));
                {
                    int pre_min = INT_MAX;
                    for (int k = i; k != j; k++){
                        pre_min = min(pre_min, bot[k]);
                    }

                    table[i][j] = max(max(top[j] - bot[j], table[i][j - 1]), top[j] - pre_min);
                }
            }
        }

        // 动态规划， 分两段求总和
        int maxsum = 0;
        int sum = 0;
        for (int i = 0; i != top.size(); i++){
            int add = 0;
            if (i < top.size() - 1)
                add = table[i + 1][top.size() - 1];
            sum = table[0][i] + add;
            if (sum > maxsum)
                maxsum = sum;
        }

        return maxsum;
    }
};

4. 大神解法

4.1 demo

一样的思路， 精简的代码

int maxProfit(vector<int> &prices) {
    int maxPro = 0;
    int minPrice = INT_MAX;
    for(int i = 0; i < prices.size(); i++){
        minPrice = min(minPrice, prices[i]);
        maxPro = max(maxPro, prices[i] - minPrice);
    }
    return maxPro;
}

4.2 demo

计算相邻两天之间的利润，如果是正收益， 就加入到整体收益中来， 这个思路果然太巧妙了！！！

int maxProfit(vector<int> &prices) {
    int ret = 0;
    for (size_t p = 1; p < prices.size(); ++p) 
      ret += max(prices[p] - prices[p - 1], 0);    
    return ret;
}

public class Solution {
public int maxProfit(int[] prices) {
    int total = 0;
    for (int i=0; i< prices.length-1; i++) {
        if (prices[i+1]>prices[i]) total += prices[i+1]-prices[i];
    }

    return total;
}

4.3 demo

4.3.1 DP

这里所用的DP 和我们的DP 不太一样， 这里的DP 和 交易的次数是关联的

class Solution {
public:
    int maxProfit(vector<int> &prices) {
        // f[k, ii] represents the max profit up until prices[ii] (Note: NOT ending with prices[ii]) using at most k transactions. 
        // f[k, ii] = max(f[k, ii-1], prices[ii] - prices[jj] + f[k-1, jj]) { jj in range of [0, ii-1] }
        // = max(f[k, ii-1], prices[ii] + max(f[k-1, jj] - prices[jj]))
        // f[0, ii] = 0; 0 times transation makes 0 profit
        // f[k, 0] = 0; if there is only one price data point you can't make any money no matter how many times you can trade
        if (prices.size() <= 1) return 0;
        else {
            int K = 2; // number of max transation allowed
            int maxProf = 0;
            vector<vector<int>> f(K+1, vector<int>(prices.size(), 0));
            for (int kk = 1; kk <= K; kk++) {
                int tmpMax = f[kk-1][0] - prices[0];
                for (int ii = 1; ii < prices.size(); ii++) {
                    f[kk][ii] = max(f[kk][ii-1], prices[ii] + tmpMax);
                    tmpMax = max(tmpMax, f[kk-1][ii] - prices[ii]);
                    maxProf = max(f[kk][ii], maxProf);
                }
            }
            return maxProf;
        }
    }
};

4.3.2 state convertion

这个方法 有点类似于状态转换的意味

First assume that we have no money, so buy1 means that we have to borrow money from others, we want to borrow less so that we have to make our balance as max as we can(because this is negative).

sell1 means we decide to sell the stock, after selling it we have price[i] money and we have to give back the money we owed, so we have price[i] - |buy1| = prices[i ] + buy1, we want to make this max.

buy2 means we want to buy another stock, we already have sell1 money, so after buying stock2 we have buy2 = sell1 - price[i] money left, we want more money left, so we make it max

sell2 means we want to sell stock2, we can have price[i] money after selling it, and we have buy2 money left before, so sell2 = buy2 + prices[i], we make this max.

So sell2 is the most money we can have.

public int maxProfit(int[] prices) {
        int sell1 = 0, sell2 = 0, buy1 = Integer.MIN_VALUE, buy2 = Integer.MIN_VALUE;
        for (int i = 0; i < prices.length; i++) {
            buy1 = Math.max(buy1, -prices[i]);
            sell1 = Math.max(sell1, buy1 + prices[i]);
            buy2 = Math.max(buy2, sell1 - prices[i]);
            sell2 = Math.max(sell2, buy2 + prices[i]);
        }
        return sell2;
    }

这个方法结合了 DP 和 状态转化的思想， 利用滚动数组实现

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int states[2][4] = {INT_MIN, 0, INT_MIN, 0}; // 0: 1 buy, 1: one buy/sell, 2: 2 buys/1 sell, 3, 2 buys/sells
        int len = prices.size(), i, cur = 0, next =1;
        for(i=0; i<len; ++i)
        {
            states[next][0] = max(states[cur][0], -prices[i]);
            states[next][1] = max(states[cur][1], states[cur][0]+prices[i]);
            states[next][2] = max(states[cur][2], states[cur][1]-prices[i]);
            states[next][3] = max(states[cur][3], states[cur][2]+prices[i]);
            swap(next, cur);
        }
        return max(states[cur][1], states[cur][3]);
    }
};