跟踪算法之一_《Robust fragments-based tracking using the integral histogram》阅读心得

最近正在研究目标跟踪，看英文文献太容易走神了，所以就把文献给翻译了出来，可能翻译的比较生硬，不喜勿喷，如有问题欢迎交流。

1.简介

        跟踪方法可以分为三类：基特征跟踪、基于轮廓跟踪、基于区域跟踪。在区域跟踪算法分类中，这几年区域跟踪算法利用直方图或其他非参数的方法进行描述（例如核参数）非常流行，最具影响力的方法可能就是meanshift算法了。

           本文作者解决了两个问题（空间信息和遮挡），通过使用部分或裂片来代替模板。之后我们首先讨论第一个问题—快速搜索定位，给一个跟踪模板，我们使用这个模板的多个矩形区域的直方图代替。通过计算目标帧的碎片的直方图，我们获得了一个碎片的投票图来描述目标的可能位置，之后对投票图进行合并，以此来获得更具有鲁棒性的方式。因为我们使用了碎片之间的空间关系，所以空间信息被利用了。当目标被遮挡时，投票图会出现一个奇异点，利用我们合并投票图的方法，我们依然能够准确定位目标的位置。

      本文提出的 基于片段跟踪规则，与之前的算法在以下几方面有所不同：

•       我们的规则对于空间遮挡具有鲁棒性； 
•       我们的规则允许使用任何度量来比较两个直方图，不仅仅分析易处理的方法像巴氏或者Equivalent Matusita metric;
•       利用投票规则空间信息被自动的利用了；
•       我们规则有自然鲁棒性，因为高效的使用了积分直方图，所以在选择多碎片/核时不用考虑太多；
•       通过大量的实验验证对于具有挑战的序列， 我们的算法也能够很好的跟踪，即使只使用灰度信息；

      我们的规则要从目标图像或目标模板中提取密度或颜色直方图。最近Porkili扩展了积分图像数据结构来替代积分直方图数据结构。我们利用这种方法来达到实时跟踪。我们扩展了文献[18]算法，对其应用到跟踪中能够实现对遮挡的正确跟踪。

2.碎片跟踪

          给以一个目标O和当前帧I，我们的目标是在当前图像中定位O。通常O通过一个特征模板图像T来表示，我们的目标是在图像帧I中定位目标的位置和目标的区域大小，这个区域与模板T非常相近。由于我们处理的是跟踪算法，假设我们有之前估计的位置和区域大小，我们就在估计的邻域内进行寻找。
          (x0，y0)是前一帧目标估计的位置，r是我们搜寻的半径 。假设PT=(dx,dy,h,w)是模板中的矩形碎片，它的中心被模板的中心(dx,dy)取代，它的半宽和半高是w、h。假设当前帧目标的位置是(x,y)，则碎片PT在当前图像中对应PI;(x,y)，它的中心是(x+dx,y+dy),它的半宽和半高是w、h。图像1对其进行了描述。

         给予碎片模板PT和相应图像碎片PI(x,y)，利用两个碎片的相似性定位目标位置(x,y)。如果d(Q,P)是计算碎片Q和碎片P的相似性，则定义

         当(x,y)在假想的范围内，我们得到VPT(,)它是与模板碎片PT相对应的投票地图。

2.1 碎片相似性计算

        我们计算碎片的相似性通过相比较灰度值或彩色直方图。与标准归一化相关性或SSD相比这种方法更灵活，虽然对于一个碎片我们只考虑它的直方图，我们可能失去了它的空间信息，但当我们使用多个碎片，碎片之间在模板空间的安排弥补了这种空间信息的缺失。

         有很多比较两个直方图的方法，最简单的比较方法是比较相应的bins。例如，一个可能使用chi-square或把直方图认为成矢量，然后对其归一化计算两个直方图的不同。Kolmogorov-smironov比较直方图的方法是通过建立每个直方图的累积分布函数，比较这两个函数。由于对测量量化到bins，使得bin-wise方法对bin附近的不同进行了平滑。

        一个更吸引人的方法是Earth Mover's Distance(EMD),在这种方法中bins的实际差异也被考虑了。它的思想是计算从第一个直方图到第二个直方图必须要移动bins的概率。所以bins的差异被使用了：例如在灰度中需要移动的概率至少是0.1从[16,32)bin 到[128,144)bin,然后移动到[32,47)bin。在第一个实例中，移动概率是被需要的，因为在分布上是不同的，在第二个示例中它可能是很简单的量化了错误。这是一种简单的线性程序的变换问题，这个问题的基础是三角的，所以这个问题可以被高效的解决。文献[20]对这个方法给予了更详细的介绍。
         我们对两个相似的计算进行了实验，第一个是原始的计算方法，假设直方图是矢量的，只是计算他们标准差。第二种是EMD计算方法。对于一个灰度图像，我们使用16bin。EMD计算方法是非常快并且对于姿态变换也没问题。对于彩色直方图，bin的数量很大(每个通道8bins，总共就要有512bins)，使用EMD我们选取K=10bins，利用最大的计数对它们进行归一化，然后使用EMD。我们使用被Rubner[19]改进的EMD。图2显示了一个片段的例子(例子中我们使用灰度信息)，我们计算的片段中心周围所有的vote map，向上30像素或向下20像素或向左或向右。图3显示vote map使用原始计算方法和EMD计算的结果。标记越黑的地方是直方图越相似的地方。EMD表面比较平滑，与原始的计算方法相比有一个最小的边界值。

3.合并vote maps

            在最后部分我们讨论怎样获得每个模板碎片PT的vote mapVPT(,)，通过给予的信息片段PT，在当前帧I中vote map在每一个可能位置(x,y)给予一个数量的分数。我们现在想合并所有模板碎片的vote map。

           我们可以简单地求vote map的和，然后寻找含有最小值的位置(vote map计算碎片的不同)。当出现遮挡时，遮挡对于求和产生了一个奇异值，导致错误估计。换句话 ，我们应该使用一个更强大的估计方法能够应对遮挡或其他原因导致的奇异点。
         一种方法是对奇异点进行定边界：

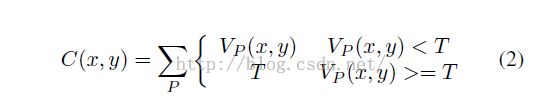
T是阈值。如果我们采用概率的视角来应对处理过程，通过变换vote map 到概率map(例如设定Lp(x,y)=K*exp(-a * Vp(x,y))，这种方法与把奇异点密度归一化然后加到真正的密度值中是等同的。C(;)最小化与获取最有可能估计的最大值获取的位置是等同的，但是不能让奇异点达到0.
        然而，我们发现对于阈值T的选择直接导致结果的很大不同，一种不同的方法是使用LMedS-type估计。对于每一个点(x,y)我们获得VP(x,y)的值，我们选择第Q个具有最小的分数值：

       参数Q更直观：它可能是碎片数量的最大值，这就是我们总期望获取线性参数的特征值。例如，如果我们保证遮挡至少能看到目标的四分之一，则我们将选择Q为碎片数量的25%。

4.使用积分直方图

          之前本文已经描述了通过多个矩形区域来获取多个直方图。通过获取的碎片模板直方图与当前目标图像多区域进行比较，能够进行处理并且达到跟踪实时性的方法是积分直方图。
        积分直方图是求取所有的像素在图像以（x,y）为中心的矩形区域内，可以计算图像的任意区域，一般选用区域的四个角的积分图像，换句话说永远选用独立的区域。
为了获取任何矩形区域的直方图，在积分直方图计算过程中，计算积分图像中每个像素落入bin的数量作为直方图的bin，通过统计积分直方图，我们能够立即计算像素在给定区域内(划分的区域是直方图的每个bin)的数量，由此我们得到了矩形区域的直方图。

        一旦积分直方图数据机构被计算完，获取区域直方图就非常简单了。因此估计当前目标的位置也相应的简单了——通过简单的比较两个直方图。

        正像之前介绍的，应用积分直方图在文献[18]中应用过。我们扩展了这种方法应用于基于部分的积分直方图。

4.1 像素分布权值

       meanshift最重要的特征是使用核函数，离目标中心越近赋予越大的权值，越远赋予越小的权值。距离目标中心较远的像素越有可能含有背景或被遮挡的信息，因此他们对直方图的贡献应该越少。然而，当使用积分直方图时，怎样把这种特征应用过来不是很清晰。

     下面的离散逼近格式可以替代连续的核权值，看图4，如果我们想获取矩形区域R的权重直方图，我们可以定义一个其内的矩形R1，用R减R1就可以获得环形R-R1的计数。这些计数和R1的统计数可以使用不同的权值，合并之后就是R的权重直方图。当然了，一个附加的内部矩形R2也可以被使用等等。

4.2 规模

       正如文献[25,18]中提到的，积分图像/直方图的优点是对于大区域和小区域计算量相差不大，所以我们搜索合适大小的目标与定位目标位置的计算量也相差不大。
       假设当前图像的目标位置是(x,y)，则碎片模板PT和图像碎片PI(x,y)，如果对当前目标假定位置添加一个区域标示s，则它就能直接的发现相应的图像碎片PI(x,y,s)：我们只是测量这个碎片的矢量位置，它的高和宽都是s。我们选用标准的方法扩大或缩小模板的10%，然后选择这个位置和规模使得公式（3）达到最小，下章将介绍使用这种方法得到的结果。

      通过文献[7]中介绍，这种方法有一些局限性。例如，如果被跟踪的目标颜色一致，则目标有一个缩小的趋势。当目标被遮挡，并且目标颜色与被遮挡物颜色一致，我们得到的结果值是目标被缩小了，并且确定它的位置在未遮挡的部分附近。应用我们的方法，我们也能得到一个合理的计数值通过保持目标在正确的尺寸，并且确定它在合适的位置。然而，也不能保证合并的vote map会比部分vote map产生更好的统计数。一个完整的处理该问题的方法是当前工作的范围。

5.结果

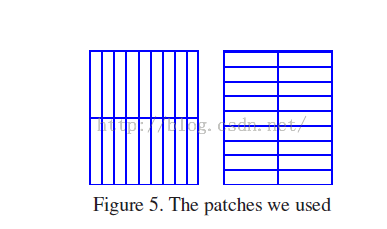
       现在我们提供我们实验的结果，在灰度图像中利用灰度的范围，直方图我们使用16bins，标记这个积分直方图数据结构需要一幅图像每一个bins，因此彩色图像的应用很消耗内存。

       我们使用水平和垂直的碎片如图5所示，这垂直的碎片是模板高的一半，模板宽的十分之一。水平碎片定义也是一个相同的方法，我们总共有36个碎片(模板中碎片的大小可稍微改变)，我们对这些碎片的选择是随意的，我们尽力使用它并寻找它。在讨论中我们又回到了这个问题。

       搜索半径是距离之前目标7像素的位置，模板在第一帧被固定了，不更新。在公式（3）中我们使用Q的25%。设定的这些参数在所有的视频序列中都是固定的。

       前两个视频显示了跟踪的鲁棒性(脸和女人)。每五帧我们人工的标记真的地面，对我们跟踪的错误进行画框，对meanshift的跟踪结果进行标记。在这两个实验中，我们跟踪的方法不会受遮挡的影响，然而meanshift跟踪会漂移走。图6和7显示了遵守ground truth的错误。图8显示了初始化模板和一些后续的帧序列。对女人视频序列的最后一帧进行标记(第二行)，可以看到使用空间信息的例子(也可以看图表题)。

       此外，我们也用一块碎片含有整个模板进行跟踪实验，结果失败了(这个例子在文献[18]中也有描述)。

       图9是下一个视频序列—生活房间。显示了姿势改变的例子，当跟踪的女人转过她的头meanshif跟踪算法漂移了，当被遮挡时目标被跟丢了。我们的跟踪对这种情况具有鲁棒性。

       图10我们显示了三个序列更多的跟踪例子，在这些跟踪序列中我们只标记我们的跟踪结果。前两组视频来自CAVIAR数据库，第一个是遮挡，第二个显示目标尺寸具有较大改变，第三个视频又是遮挡。利用这些我们可以证明我们的跟踪怎样使用空间信息(在基于直方图方法中他一般会被跟丢)，这两个人在全局上具有相似的直方图信息(半黑半白)，我们的跟踪方法知道白色的像素是在目标的上半部分，所以当两个人走的很近的时候，他还能跟上不会漂移。

6.讨论和结论

           本文我们提出了一个新颖的方法(fragtrack)进行目标跟踪，我们的方法采用积分直方图，对基于片段表示模板和从识别目标的voting进行合并。对于遮挡和目标姿态变换都能够进行实时跟踪。与其它跟踪方法相比，我们的跟踪方法更自由：碎片的选择是随机的，并且不需要目标的先验知识。

            没有积分直方图的高效的数据结构也就不能计算出每个碎片的vote map，换句话说，不使用碎片规则，对于遮挡和姿态变换也不会有这么好的跟踪效果。对于下一步工作还有很多要做，第一个问题就是模板更新，我们想要避免遮挡被加入模板中，使用多个相似计数值的碎片可能解决这个问题。第二个问题是当使用模块大小时部分与完全困境解析在[7]之前被描述了，这个问题在部分遮挡下更明显。最后，我们也考虑不连通的矩形片段，并选用最能代表跟踪目标的片段。