HDU 4288 Coder 离散化+线段树
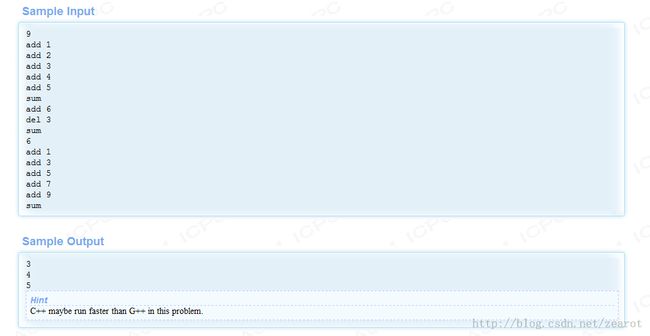
题意:对一个集合进行插入与删除操作。要求询问某个时刻,集合中的元素从小到大排序之后,序号%5 ==3 的元素值之和。
首先元素的值可以达到10^9 所以,首先离散化,将所有可能的元素值映射到正整数。
然后线段树的话,用index 存当前节点 所含的元素数量。
用 D [R] 存 所含的元素中,序号%5 ==R 的元素值之和。
则可以用左右子树的这些信息来求出本节点的这些信息,具体见代码。
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include <map>
#define maxn 100010
using namespace std;
//记录操作
int n;
int op[maxn];
//离散化
int cnt;
struct A{
int index;
int value;
void Set(int I,int V){index=I;value=V;}
bool operator<(const A&B)const{return value<B.value;}
}h[maxn];
map<int,int>MP;
//线段树
struct Node{
int index;
long long D[5];
void clear(){index=0;memset(D,0,sizeof(D));}
void show(){
printf("index:%d \n%d %d %d %d %d \n",index,D[0],D[1],D[2],D[3],D[4]);
}
}H[maxn<<2];
void PushUp(int rt){
H[rt].index=H[rt<<1].index+H[rt<<1|1].index;
for(int r=0;r<5;++r){
H[rt].D[r]=H[rt<<1].D[r]+H[rt<<1|1].D[(r+5-(H[rt<<1].index%5))%5];
}
}
void build(int l,int r,int rt){
if(l==r){
H[rt].clear();
return;
}
int m=(l+r)>>1;
build(l,m,rt<<1);
build(m+1,r,rt<<1|1);
PushUp(rt);
}
void Add(int X,int C,int l,int r,int rt){
if(l==r){
H[rt].clear();
H[rt].index=1;
H[rt].D[1]=C;
return;
}
int m=(l+r)>>1;
if(X <= m) Add(X,C,l,m,rt<<1);
if(X > m) Add(X,C,m+1,r,rt<<1|1);
PushUp(rt);
}
void Del(int X,int l,int r,int rt){
if(l==r){
H[rt].clear();
return;
}
int m=(l+r)>>1;
if(X <= m) Del(X,l,m,rt<<1);
if(X > m) Del(X,m+1,r,rt<<1|1);
PushUp(rt);
}
int main(void)
{
while(~scanf("%d",&n)){
cnt=0;MP.clear();
//记录操作
for(int i=0;i<n;++i){
char Op[5];
scanf("%s",Op);
switch(Op[0]){
case 'a':
scanf("%d",&op[i]);
if(!MP.count(op[i])){
++cnt;
h[cnt].Set(cnt,op[i]);
MP[op[i]]=1;
}
break;
case 'd':scanf("%d",&op[i]);op[i]=-op[i];break;
case 's':op[i]=0;break;
default:break;
}
}
//离散化
sort(h+1,h+cnt+1);
for(int i=1;i<=cnt;++i){
MP[h[i].value]=i;
}
build(1,cnt,1);
//线段树
for(int i=0;i<n;++i){
if(op[i]){
if(op[i]>0){
Add(MP[op[i]],op[i],1,cnt,1);
}
else{
Del(MP[-op[i]],1,cnt,1);
}
}
else{
cout<<H[1].D[3]<<endl;
}
}
}
return 0;
}