POJ 2482 Stars in Your Window (线段树扫描线)

题意：

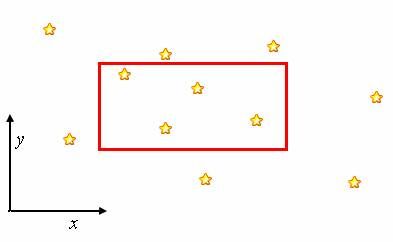
给定n个星星的坐标(x,y)以及亮度c ,求用一个宽W,高H的框（不含边界），能框住的星星的亮度总和的最大值为多少。

( 0<= x,y <2^31 , 1<=c<=100    , 1<=W , H <= 1000000    ,   x,y,c,W,H都是整数)

思路：

用矩形右上角坐标（X,Y）来代表矩形位置，原问题等价于，X,Y为整数，用一个宽W,高H的框（不含左，下边界），能框住的星星的亮度总和的最大值为多少。因为，若X,Y为整数，并且四边上都有星星，那么将该方框向右和上分别平移1/2个单位，就可以在不丢失框内星星的情况下框进上边框和右边框的星星。

转换之后，对于星星(x,y),矩形的右上角坐标的范围在 x-[x,x+W), y-[y,y+H) 这个区域内时，算作框进了这颗星星，要算上这颗星星的亮度。

于是，星星变成了带权值的矩形，矩形框变成了点，问题就是在矩形的重合图中，找到权值最大的点。

这就可以用线段树扫描线了，就是，用一条垂直于x轴的线来从左到右扫描整个图形。整个扫描过程中，线上权值最大的一点就是答案。

线上的权值需要进行区间修改以及维护最大值，这里就用线段树来储存。

将Y值离散化（去除重复值），然后，将星星先根据X值，再根据Y值排序。

然后不断将新的矩形加入，旧的矩形删除就行了。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define  inf  0x1fffffff
#define maxn 20007
#define LL long long
using namespace std;
//SBT 离散化 
LL Rank[maxn],Rn;
void SetRank(){
	sort(Rank+1,Rank+1+Rn); 
	int I=1;
	for(int i=2;i<=Rn;++i) if(Rank[i]!=Rank[i-1]) Rank[++I]=Rank[i];
	Rn=I;
} 
int GetRank(LL x){
	int L=1,R=Rn,M;//[L,R] first >=x
	while(L!=R){
		M=(L+R)>>1;
		if(Rank[M]<x) L=M+1;
		else R=M;
	}
	return L;
}
//储存数据 
struct Star{//记录星星，之后要排序 
	LL x,y;int c;
	Star(){}
	Star(LL x,LL y,int c):x(x),y(y),c(c){}
	bool operator < (const Star &B)const{
		return x < B.x|| x==B.x && y < B.y;
	}
}St[maxn>>1];
int n,W,H;
//线段树 区间加&&最大值 
int Max[maxn<<2],Add[maxn<<2];
void PushUp(int rt){
	Max[rt]=max(Max[rt<<1],Max[rt<<1|1]);
}
void PushDown(int rt){
	if(Add[rt]){
		Add[rt<<1]+=Add[rt];Add[rt<<1|1]+=Add[rt];
		Max[rt<<1]+=Add[rt];Max[rt<<1|1]+=Add[rt];
		Add[rt]=0;
	}
}
void Update(int L,int R,int C,int l,int r,int rt){
	if(L <=l && r <= R){Add[rt]+=C;Max[rt]+=C;return;}
	PushDown(rt);
	int m=(l+r)>>1;
	if(L <= m) Update(L,R,C,l,m,rt<<1);
	if(R >  m) Update(L,R,C,m+1,r,rt<<1|1); 
	PushUp(rt);
}
int main(void)
{
	while(~scanf("%d%d%d",&n,&W,&H)){
		memset(Max,0,sizeof(Max));
		memset(Add,0,sizeof(Add));
		Rn=0;
		for(int i=1;i<=n;++i) {
			scanf("%I64d%I64d%d",&St[i].x,&St[i].y,&St[i].c);
			Rank[++Rn]=St[i].y;
			Rank[++Rn]=St[i].y+H;
		}
		SetRank();
		sort(St+1,St+n+1);//给星星排序 
		int L=1,X,ANS=0;
		for(int i=1;i<=n;++i){
			Update(GetRank(St[i].y),GetRank(St[i].y+H)-1,St[i].c,1,Rn,1);//加入新矩形 
			X=St[i].x;//更新当前X 
			while(St[L].x+W <= X){//删除已经对横坐标为X的扫描线无影响的矩形 
				Update(GetRank(St[L].y),GetRank(St[L].y+H)-1,-St[L].c,1,Rn,1);
				++L;
			}
			ANS=max(ANS,Max[1]);//求最大值 
		}
		printf("%d\n",ANS);//输出答案 
	}
return 0;
}