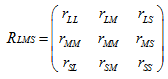颜色迁移之五——自适应迁移算法

颜色空间为一个三维的线性空间，通常使用红色、绿色和蓝色（RGB）作为颜色空间的基，但这三原色不能直观地度量色调、饱和度和亮度（HSV），为了体现颜色空间中的不同特性，人们总结了很多颜色空间。由Smith等提出的LMS颜色空间的三个分量分别表示长、中、短激发光谱。而人的视网膜中锥状细胞的光感器对光的波长最敏感。在这个意义上，我们把计算机里的RGB图像表示转换成基于人眼更为敏感波长的LMS表示。实际上不同颜色空间是同构的，因此它们之间必然存在变换矩阵，事实上在Reinhard等给出了RGB和LMS之间的颜色变换，经过变换后的LMS值的分布域和RGB 值的分布域一样，还是比较发散，为了使得LMS数据点更加聚敛，Reinhard等对LMS做了对数变换L=logL，M=logM，S=logS来代替LMS的值。胡国飞等在此基础上求出了LMS的相关矩阵

，

其中r_LM，r_MS，r_LS分别表示L和M，M和S，L和S的相关系数。大量图像样本的实验结果表明相关矩阵通常不是一个三对角矩阵，甚至根本不是对角占优的矩阵，也就是说LMS三个分量间具有严重的相关性。然后利用特征值分析和主元分析方法来得到复合线性变换矩阵，对LMS值采取一系列平移旋转和变比的线性变换，使得所得的图像各像素的颜色分量基本上消除这种相关性。根据矩阵论，很容易地对相关矩阵进行特征值分解，求出特征值λ1，λ2，λ3和特征向量e1，e2，e3，并记特征矩阵为

，

然后由求出负载因子矩阵，接着就可以求出LMS到lαβ颜色空间的基向量的过渡矩阵（其中为特征值矩阵的逆），这个C就是要求的复合变换矩阵，即。

对每一幅欲处理的图像，都有不同的过渡矩阵C。利用对自适应的处理颜色图像和形状图像所得到的和，分别求出各自的lαβ颜色空间上的值。而不是利用一个固定的C来处理所有的图像。虽然此算法在运算时间上付出一点代价，自适应的方法更符合图像本身的颜色分布。另外，对一幅图像的所有像素进行处理可以增加统计量的精确度，但是出于计算速度和存储资源考虑，也可以间隔采样以减少处理的数据量，而不影响整体效果。

——————————————————————————————————————-——————————————————————

用的一些函数，其他的大部分参考我之前写的Reinhard算法的给出代码

//矩阵求特征值与特征向量
bool JacbiCor(double *pMatrix,int nDim, double *pdblVects, double *pdbEigenValues, double dbEps,int nJt)  
{  
	for(int i = 0; i < nDim; i ++)   
	{     
		pdblVects[i*nDim+i] = 1.0f;   
		for(int j = 0; j < nDim; j ++)   
		{   
			if(i != j)     
				pdblVects[i*nDim+j]=0.0f;   
		}   
	}   

	int nCount = 0;     //迭代次数  
	while(1)  
	{  
		//在pMatrix的非对角线上找到最大元素  
		double dbMax = pMatrix[1];  
		int nRow = 0;  
		int nCol = 1;  
		for (int i = 0; i < nDim; i ++)          //行  
		{  
			for (int j = 0; j < nDim; j ++)      //列  
			{  
				double d = fabs(pMatrix[i*nDim+j]);   

				if((i!=j) && (d> dbMax))   
				{   
					dbMax = d;     
					nRow = i;     
					nCol = j;   
				}   
			}  
		}  

		if(dbMax < dbEps)     //精度符合要求   
			break;    

		if(nCount > nJt)       //迭代次数超过限制  
			break;  

		nCount++;  

		double dbApp = pMatrix[nRow*nDim+nRow];  
		double dbApq = pMatrix[nRow*nDim+nCol];  
		double dbAqq = pMatrix[nCol*nDim+nCol];  

		//计算旋转角度  
		double dbAngle = 0.5*atan2(-2*dbApq,dbAqq-dbApp);  
		double dbSinTheta = sin(dbAngle);  
		double dbCosTheta = cos(dbAngle);  
		double dbSin2Theta = sin(2*dbAngle);  
		double dbCos2Theta = cos(2*dbAngle);  

		pMatrix[nRow*nDim+nRow] = dbApp*dbCosTheta*dbCosTheta +   
			dbAqq*dbSinTheta*dbSinTheta + 2*dbApq*dbCosTheta*dbSinTheta;  
		pMatrix[nCol*nDim+nCol] = dbApp*dbSinTheta*dbSinTheta +   
			dbAqq*dbCosTheta*dbCosTheta - 2*dbApq*dbCosTheta*dbSinTheta;  
		pMatrix[nRow*nDim+nCol] = 0.5*(dbAqq-dbApp)*dbSin2Theta + dbApq*dbCos2Theta;  
		pMatrix[nCol*nDim+nRow] = pMatrix[nRow*nDim+nCol];  

		for(int i = 0; i < nDim; i ++)   
		{   
			if((i!=nCol) && (i!=nRow))   
			{   
				int u = i*nDim + nRow;  //p    
				int w = i*nDim + nCol;  //q  
				dbMax = pMatrix[u];   
				pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta;   
				pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta;   
			}   
		}   

		for (int j = 0; j < nDim; j ++)  
		{  
			if((j!=nCol) && (j!=nRow))   
			{   
				int u = nRow*nDim + j;  //p  
				int w = nCol*nDim + j;  //q  
				dbMax = pMatrix[u];   
				pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta;   
				pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta;   
			}   
		}  

		//计算特征向量  
		for(int i = 0; i < nDim; i ++)   
		{   
			int u = i*nDim + nRow;      //p     
			int w = i*nDim + nCol;      //q  
			dbMax = pdblVects[u];   
			pdblVects[u] = pdblVects[w]*dbSinTheta + dbMax*dbCosTheta;   
			pdblVects[w] = pdblVects[w]*dbCosTheta - dbMax*dbSinTheta;   
		}   

	}  

	for(int i = 0; i < nDim; i ++)   
			pdbEigenValues[i] = pMatrix[i*nDim+i];   

	//设定正负号  
	for(int i = 0; i < nDim; i ++)   
	{  
		double dSumVec = 0;  
		for(int j = 0; j < nDim; j ++)  
			dSumVec += pdblVects[j * nDim + i];  
		if(dSumVec<0)  
		{  
			for(int j = 0;j < nDim; j ++)  
				pdblVects[j * nDim + i] *= -1;  
		}  
	}  
	return 1;
}

//矩阵求逆
void InverseMatrix(double A[3][3],double B[3][3],int n)
{
	int i,j,k,m=2*n;
	double mik,temp;
	double a[3][6]={0};

	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			if(i==j)
				B[i][j]=1.0;
			else
				B[i][j]=0.0;
		}
	}        //初始化B=E

	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			a[i][j]=A[i][j];  //复制A到a，避免改变A的值
	for(i=0;i<n;i++)
		for(j=n;j<m;j++)
			a[i][j]=B[i][j-n];  //复制B到a，增广矩阵

	for(k=1;k<=n-1;k++)
	{
		for(i=k+1;i<=n;i++)
		{
			mik=a[i-1][k-1]/a[k-1][k-1];
			for(j=k+1;j<=m;j++)
			{
				a[i-1][j-1]-=mik*a[k-1][j-1];
			}
		}
	}        //顺序高斯消去法化左下角为零

	for(i=1;i<=n;i++)
	{
		temp=a[i-1][i-1];
		for(j=1;j<=m;j++)
		{
			a[i-1][j-1]/=temp;
		}
	}        //归一化

	for(k=n-1;k>=1;k--)
	{
		for(i=k;i>=1;i--)
		{
			mik=a[i-1][k];
			for(j=k+1;j<=m;j++)
			{
				a[i-1][j-1]-=mik*a[k][j-1];
			}
		}
	}        //逆序高斯消去法化增广矩阵左边为单位矩阵

	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			B[i][j]=a[i][j+n];  //取出求逆结果

	for(i=0;i<n;i++)
		for(j=0;j<n;j++)
			if(fabs(B[i][j])<0.0001)
				B[i][j]=0.0;
}

——————————————————————————————————————-——————————————————————

参考文献：胡国飞, 傅健, 彭群生. 自适应颜色迁移[J]. 计算机学报, 2004,27(9):1245-1249.