七、快速排序
快速排序
快速排序引人注目的特点包括它是原地排序(只需要一个很小的辅助栈),且将长度为N的数组排序所需的时间和NlogN成正比。之前的算法都无法结合这两个优点。
另外快速排序的内循环比大多数排序算法都要短小,这意味着它无论是在理论上还是在实际中都要更快。缺点是有可能会导致平方级别
基本算法
快速排序是一种分治的排序算法。它将一个数组分成两个数组,将两部分独立地排序。快速排序和归并排序是互补的;归并排序将数组分成两个子数组分别排序,并将有序的子数组归并以将整个数组排序;而快速排序将数组排序的方式则是当两个子数组都有序时整个数组自然有序了。
先给出代码:
public class Quick {
// This class should not be instantiated.
private Quick() { }
public static void sort(Comparable[] a) {
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
assert isSorted(a);
}
// quicksort the subarray from a[lo] to a[hi]
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
assert isSorted(a, lo, hi);
}
// partition the subarray a[lo..hi] so that a[lo..j-1] <= a[j] <= a[j+1..hi]
// and return the index j.
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo;
int j = hi + 1;
Comparable v = a[lo];
while (true) {
// find item on lo to swap
while (less(a[++i], v))
if (i == hi) break;
// find item on hi to swap
while (less(v, a[--j]))
if (j == lo) break; // redundant since a[lo] acts as sentinel
// check if pointers cross
if (i >= j) break;
exch(a, i, j);
}
// put partitioning item v at a[j]
exch(a, lo, j);
// now, a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
return j;
}
public static Comparable select(Comparable[] a, int k) {
if (k < 0 || k >= a.length) {
throw new IndexOutOfBoundsException("Selected element out of bounds");
}
StdRandom.shuffle(a);
int lo = 0, hi = a.length - 1;
while (hi > lo) {
int i = partition(a, lo, hi);
if (i > k) hi = i - 1;
else if (i < k) lo = i + 1;
else return a[i];
}
return a[lo];
}
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
private static boolean isSorted(Comparable[] a) {
return isSorted(a, 0, a.length - 1);
}
private static boolean isSorted(Comparable[] a, int lo, int hi) {
for (int i = lo + 1; i <= hi; i++)
if (less(a[i], a[i-1])) return false;
return true;
}
// print array to standard output
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.println(a[i]);
}
}
public static void main(String[] args) {
String[] a = StdIn.readAllStrings();
Quick.sort(a);
show(a);
// shuffle
StdRandom.shuffle(a);
// display results again using select
StdOut.println();
for (int i = 0; i < a.length; i++) {
String ith = (String) Quick.select(a, i);
StdOut.println(ith);
}
}
}示意图(字母的顺序为大小,先左后右地展示分治):
相当于每一次选定一个元素(一般是第一个,下图中的黑体所示),然后通过比较,交换,让这个数据成为一个分界线,左边的比他小,右边的比他大,然后针对左右两部分再这样干,最终数据就排好了。

该方法的关键在于切分,这个过程使得数组满足下面三个条件:
1. 对于某个j,a[j]已经排定;
2. a[lo]到a[j-1]中的所有元素都不大于a[j]
3. a[j+1]到a[hi]中的所有元素都不小于a[j]
如此递归地切分。
切分示意图:
一般的策略是先取a[lo]作为切分元素,,然后我们从数组的左端开始向右扫描直到找到一个大于等于它的元素,再从数组的右端开始向左扫描直到找到一个小于等于它的元素,然后交换。如此继续,当两个指针要相遇时,只需要交换a[lo]和a[j]返回j即可。
切分轨迹:展示了一次partition

可以看到最后K放在了合适的地方,然后再分治,递归。
注意:
1. 原地切分,使用辅助数组开销大
2. 不要越界,
3. 保持随机性,本算法是先打乱的(StdRandom.shuffle),当然,另一种保持随机性的方法就是随机选取分界元素
4. 要终止循环
5. 处理切分元素有重复的情况
如算法所示,左侧扫描最好是在遇到大于等于切分元素值的元素时停下,右侧扫描则是遇到小于等于切分元素值的元素时停下。这样能够避免运行时间变为平方级别。
6. 终止递归
性能特点
快速排序的缺点:在切分不平衡时整个程序可能会极为低效。例如第一次从第一小的元素切分,第二次从第二小的元素切分,如此这般

虽然快速排序和归并排序的复杂度差不多,但是一般快速排序会更快,因为它移动的次数更少。
算法改进
切换到插入排序
和大多数排序算法一样,改进快速排序的一个简单办法基于以下两点:对于小数组,快速排序被插入排序慢; 因为递归,快速排序的sort()方法在小数组中也会调用自己简单的改动:将sort中的:
if(hi<=lo) return;改成
if(hi<=lo+M) { Insert.sort(a,lo,hi); return;}三取样切分
改进快速排序性能的第二个办法是使用子数组的一小部分元素的中位数来切分数组。人们发现将采样大小设为3并且大小剧中的元素切分效果最好。代价是要计算中位数熵最优的排序
实际应用中会经常出现含有大量重复元素的数组,例如我们可能需要将大量人员资料按照生日排序,或者按照性别区分开来。此时可以进行一些改进,例如一个元素全部重复的子数组就不需要再排序了,但我们的算法还会继续将它切分为更小的数组。在有大量重复元素的情况下,快速排序的递归性会使元素全部重复的子数组经常出现,这就有很大的改进潜力,将当前实现的线性对数级别的性能提高到线性级别。一个简单的实现是将数组切分成三部分,分别对应小于、等于和大于切分元素的数组元素。
a[lo…lt-1]中的元素都小于v
a[gt+1..hi]中的元素都大于v
a[lt..i-1]中的元素都等于v
a[i..gt]中的元素都还未确定。如下图所示:
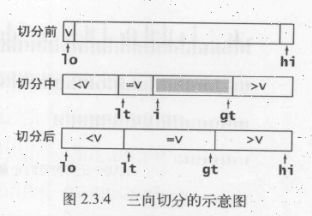
这些操作都会保证数组元素不变且缩小gt-I的值(这样循环才会结束)。另外,除非和切分元素相等,其他元素都会被交换。这种算法在应对含有重复元素较多的情况下会比归并排序更快
熵最优即三向切分算法分析:
public class Quick3way {
// This class should not be instantiated.
private Quick3way() { }
public static void sort(Comparable[] a) {
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
assert isSorted(a);
}
// quicksort the subarray a[lo .. hi] using 3-way partitioning
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int lt = lo, gt = hi;
Comparable v = a[lo];
int i = lo;
while (i <= gt) {
int cmp = a[i].compareTo(v);
if (cmp < 0) exch(a, lt++, i++);
else if (cmp > 0) exch(a, i, gt--);
else i++;
}
// a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi].
sort(a, lo, lt-1);
sort(a, gt+1, hi);
assert isSorted(a, lo, hi);
}
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
// does v == w ?
private static boolean eq(Comparable v, Comparable w) {
return v.compareTo(w) == 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
private static boolean isSorted(Comparable[] a) {
return isSorted(a, 0, a.length - 1);
}
private static boolean isSorted(Comparable[] a, int lo, int hi) {
for (int i = lo + 1; i <= hi; i++)
if (less(a[i], a[i-1])) return false;
return true;
}
// print array to standard output
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.println(a[i]);
}
}
public static void main(String[] args) {
String[] a = StdIn.readAllStrings();
Quick3way.sort(a);
show(a);
}
}所以这里称为 熵最优
注意:当所有的主键均不重复时有H=lgN(所有主键的概率均为1/N)。三向切分的最坏情况证实所有的主键均不相同。当存在重复主键时,它的性能就会比归并排序好得多。这两个性质说明了三向切分是信息量最优的,即对任意分布的输入,最优的基于比较的算法平均所需要的比较次数和三向切分的快速排序平均所需的比较次数相互处于常数因子范围之内。三向切分算法对于包含大量重复元素的数组,它将排序时间从线性对数级别降低到了线性级别。
没有基于比较的排序算法能够用少于信息量决定的比较次数完成排序。

