九、排序算法的应用(找中位数、重复统计、Kendall tau距离等)
- 应用
- 将各种数据排序
- 该使用哪种排序算法
- 问题的归约
- 找出数组中重复元素
- 排名
- 优先队列
- 中位数与顺序统计
应用
将各种数据排序
注意:想在忽略大小写的情况下比较字符串进行排序,可以使用Java类型中定义的CASE_INSENSITIVE比较器,例如:Insertion.sort(a, String.CASE_INSENSITIVE_ORDER)
排序的稳定性:如果一个排序算法能够保留数组中重复元素的相对位置则可以被称为是稳定的。目前稳定的算法(插入排序和归并排序),不稳定的(选择、希尔、快速、堆排序)
稳定性的说明:

该使用哪种排序算法
几种排序算法比较

其中快速排序较优:

但如果稳定性很重要,归并排序可能是最好的- java系统库的排序
主要是Arrays.sort()方法
java程序员选择对原始数据类型使用了(三向切分)的快速排序,对引用类型使用了归并排序。前者看重速度和空间,后者看重稳定性。
- java系统库的排序
问题的归约
归约指的是为解决某个问题而发明的算法正好可以用来解决另一个问题。例如,很多问题如果暴力破解可能是平方级别,但是通过排序之后再解决就是线性级别了。
找出数组中重复元素
可以用平方级别一个个对比一遍,也可以先排序,然后记录重复的元素:
例如统计不重复元素的个数
Qucik.sort(a);
int count = 1;
for(int i = 1; i< a.length; i++){
if(a[i].compareTo(a[i-1] != 0)
count ++;排名
Kendall tau距离:两组排列之间的顺序不同的数对的数量。
某个排列和标准排列的Kendall tau距离就是逆序对数量,可以通过插入排序设计一个平方级别的算法计算这个距离(详见插入排序)。无代码
优先队列
例如找出M个最大的元素(TopM)以及合并输入流(Multiway)这种应用都可以应用优先队列。合并输入流之前已给,这里给出TopM的代码(内部使用了一个优先队列):
public static void main(String[] args) {
int M = Integer.parseInt(args[0]);
MinPQ<Transaction> pq = new MinPQ<Transaction>(M+1);
while (StdIn.hasNextLine()) {
// Create an entry from the next line and put on the PQ.
String line = StdIn.readLine();
Transaction transaction = new Transaction(line);
pq.insert(transaction);
// remove minimum if M+1 entries on the PQ
if (pq.size() > M)
pq.delMin();
} // top M entries are on the PQ
// print entries on PQ in reverse order
Stack<Transaction> stack = new Stack<Transaction>();
for (Transaction transaction : pq)
stack.push(transaction);
for (Transaction transaction : stack)
StdOut.println(transaction);
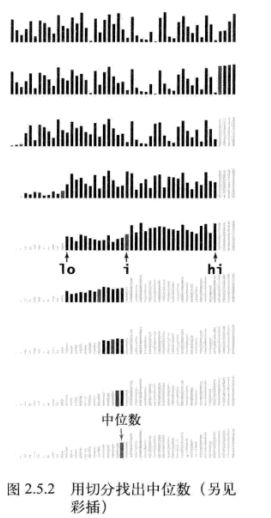
} 中位数与顺序统计
找中位数是找到一组数中的第k小元素的特殊情况
当k很小或很大时找出数组中的k歌最小值都很简单,但当k和数组大小成一定比例时任务就变得比较困难(例如k=N/2)。
比较快的找中位数代码:
其中partition是快速排序的切割方法
public class findMedian {
public static Comparable select(Comparable[] a, int k){
//打乱数组,因为快速排序跟输入出现的概率有关
StdRandom.shuffle(a);
int lo = 0, hi = a.length-1;
while(hi>lo){
int j = partition(a, lo, hi);
if (j == k) return a[k];
else if (j > k) hi = j - 1;
else if (j< k) lo = j + 1;
}
return a[k];
}
private static <T> int partition(Comparable[] a, int lo, int hi) {
int i = lo;
int j = hi + 1;
Comparable v = a[lo];
while (true) {
// find item on lo to swap
while (less(a[++i], v))
if (i == hi) break;
// find item on hi to swap
while (less(v, a[--j]))
if (j == lo) break; // redundant since a[lo] acts as sentinel
// check if pointers cross
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
private static <T> void exch(Comparable[] a, int i, int j) {
// TODO Auto-generated method stub
int temp = (int) a[i];
a[i] = a[j];
a[j] = temp;
}
private static <T> boolean less(Comparable a, Comparable v) {
// TODO Auto-generated method stub
if (a.compareTo((T) v)<0) return true;
return false;
}
public static void main(String[] args) {
Comparable[] a = {8,0,5,1,4,5,7,2};
int k = a.length/2;
System.out.println(select(a, k));
System.out.println(Arrays.toString(a));
}
}