http://www.notonlysuccess.com/index.php/aho-corasick-automaton/
后缀自动机学习总结
后缀自动机(FHQ+Neroysq补完)
字典树上建失败指针什么的。
一个比较好的方法是稍微修改一下next的定义。
原来next[i][j]表示字典树中i节点的字符为j的儿子节点编号。
现在拓展一下。如果i节点没有字符为j的儿子,那么next[i][j]就是i节点沿着失败指针一直走到有字符为j的儿子的节点编号,如果没有,那么就指向根。
相当于是一个路径压缩的思想吧。这样一来,建立完自动机后,next指针就是很直接的转移关系了,不需要再特意的沿着失败指针跑啊跑的。
这种写法实现起来和用起来都很
===================分割线============================
Aho–Corasickautomaton
AC automaton嘛,感觉上就是trie与kmp的合体,感觉两者实际上是同一个东西,只是kmp是单串的,ac automaton是多串的,思想是差不多的。
对于ac automaton的总结,个人觉得这个是比较好学的。trie大家肯定是能随便建的嘛,fail指针一加上就成了ac automaton了,还是比较方便的哈,不过我写的ac automaton代码是比较孬的那种,每次都要对root做一个特殊讨论的,后面发现如果加一个辅助结点,让这个结点的所有next指向root,root->fail指向这个结点,代码一下简洁多了,大家有兴趣的话可以去试试。
ac automaton,我主要看到了两个版本,感觉都各有好处,一种是建完树以后,只建fail指针,不再对next做处理,我最开始就是写的这种方法,感觉还是不错的,另一种就是在建fail的时候还对每个结点的next也做一些相应的处理,这样写的话,在匹配的时候就会感觉特别方便,而且有些和dp、矩阵快乘相关的题上,这样写也会比较方便。不过感觉上初学的话还是第一种比较好。
ac automaton 的话,还可以解决一个问题,那就是一个带有‘?’的模式串的问题,关于这个问题这里有详细讲解
HDU 3901 Wildcard AC自动机通配符匹配(提醒:对于内存开得刚刚好的acmer,此题串长没有严格小于10^5,但小于10^5+11)
个人感觉这一点,基本上打破了我一直以来对ac自动机的理解,我一直以为只有当要多串匹配时才需要ac自动机,而现在就算是单串,也可能需要ac自动机了。虽然实质上这里还是多串匹配,但至少从思维上来说,以后的思维宽度可能会更宽了,
suffix arrays 后缀数组吧,学完后回想起来,感觉还是比较好学的,我基本就是靠看《后缀数组——处理字符串的有力工具》-罗穗骞—09这篇论文入门的,个人感觉讲得还是挻好的,虽然我当时看了很久才大概明白了一点倍增算法的思想,关于dc3完全不懂,
我觉得这篇论文在后面给我练习相当好,给出了很后缀数组应用的例子,在使用了几次之后,也就基本明白后缀数组倍增算法了。
在这里推荐一下昀昀放的一套题呀啦那一卡(字符串专题) http://acm.hust.edu.cn:8080/judge/contest/view.action?cid=1496#overview ,这套题个人感觉相当不错的,对于匹配来说是很好的练习。个人对学了后缀数组的感觉就重在练习与使用上了。
suffix tree
这个东西吧,我也是前不久才学的,只学了一点点,不过感觉上如果之前会后缀数组和ac自动机的话感觉上学起来好学一点,不过现在感觉上整个人是比较浮躁的。现在感觉自己想静下心来看点东西感觉比较困难的样子了。
后缀树的话,我觉得这篇论文讲得还是比较不错的《On–line construction of suffix trees》,至少实现的代码比较短,我就是按里面写的伪代码实现的。不过由于各种原因,当时这篇论文我看了一周才基本明白suffix tree。
好不容易学了suffix tree,去写fzu的(Problem 1916 Harmonious Substring Function—— http://acm.fzu.edu.cn/problem.php?pid=1916 )一把就MLE了。还需要多加学习啊。
字符串哈希
RK实际上就是基于hash的,个人感觉RK还是很实用的,偶尔遇到一些比较难的题,用RK暴一暴居然就过了,太神了,不过RK的思想非常简单了,而且也是人人都能写的那种,如果在想不出一个复杂度比较好的算法时,可以用RK试试。关于RK还有几点:经常听见有人说单hash不靠谱,不过个人感觉这个比较靠人品吧,我一般就是单hash的,挂的次数还是比较少的,实在不行,换两个模数一般问题还是不大的。还有,关于hash之后的查找串,我记得有一次我把这个功能写成一个函数,然后就T了,后面看别人的代码,他把这个写在查找的那个地方,没有写成函数,我也这样改,然后就过了。以致于以后我都这样写,不过我总觉得这样是一个不好的习惯。大家看着办吧,RK如果T了的话,可以试试。
===================================我是分割线啦啦啦==============================
原文
关键字:AC自动机 自动机 有限状态自动机 Trie 字母树 字符串匹配 多串匹配算法
Note:阅读本文需要有KMP算法基础。
AC自动机是用来处理多串匹配问题的,即给你很多串,再给你一篇文章,让你在文章中找这些串是否出现过,在哪出现。也许你考虑过AC自动机名字的含义,我也有过同样的想法。你现在已经知道KMP了,他之所以叫做KMP,是因为这个算法是由Knuth、Morris、Pratt三个提出来的,取了这三个人的名字的头一个字母。那么AC自动机也是同样的,他是Aho-Corasick。所以不要再YY地认为AC自动机是AC(cept)自动机,虽然他确实能帮你AC一点题目。
。。。扯远了。。。
要学会AC自动机,我们必须知道什么是Trie,即字母树。如果你会了,请跳过这一段
Trie是由字母组成的。
这就是一棵Trie树。用绿色标出的点表示一个单词的末尾(为什么这样表示?看下去就知道了)。树上一条从root到绿色节点的路径上的字母,组成了一个“单词”。
/* 也许你看了这一段,就知道如何构建Trie了,那请跳过以下几段。*/
那么如何来构建一棵Trie呢?就让我从一棵空树开始,一步步来构建他。
一开始,我们有一个root:
现在,插入第一个单词,she。这就相当于在树中插入一条链。过程很简单。插完以后,我们在最后一个字母’e’上加一个绿色标记,结果如图:
再来一个单词,shr(什么词?…..右位移啊)。由于root下已经有’s’了,我们就不重复插入了,同理,由于’s’下有’h’了,我们也略过他,直接在’h’下插入’r’,并把’r’标为绿色。结果如图:
按同样的方法,我们继续把余下的元素插进树中。
最后结果:
也就是这样:
好了,现在我们已经有一棵Trie了,但这还不够,我们还要在Trie上引入一个很强大的东西:失败指针或者说shift数组或者说Next函数 …..你爱怎么叫怎么叫吧,反正就是KMP的精华所在,这也是我为什么叫你看KMP的原因。
KMP中我们用两个指针i和j分别表示,A[i-j+ 1..i]与B[1..j]完全相等。也就是说,i是不断增加的,随着i的增加j相应地变化,且j满足以A[i]结尾的长度为j的字符串正好匹配B串的前 j个字符,当A[i+1]<>B[j+1],KMP的策略是调整j的位置(减小j值)使得A[i-j+1..i]与B[1..j]保持匹配且新的B[j+1]恰好与A[i+1]匹配(从而使得i和j能继续增加)。
Trie树上的失败指针与此类似。
假设有一个节点k,他的失败指针指向j。那么k,j满足这个性质:设root到j的距离为n,则从k之上的第n个节点到k所组成的长度为n的单词,与从root到j所组成的单词相同。
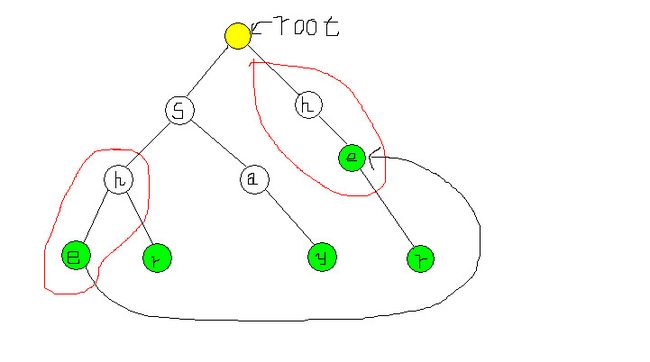
比如图中she中的’e’的失败指针就应该指向her中的’e’。因为:
图中红框部分是完全一样的。
那么我们要怎样构建这个东西呢?其实我们可以用一个简单的BFS搞定这一切。
对于每个节点,我们可以这样处理:设这个节点上的字母为C,沿着他父亲的失败指针走,直到走到一个节点,他的儿子中也有字母为C的节点。然后把当前节点的失败指针指向那个字目也为C的儿子。如果一直走到了root都没找到,那就把失败指针指向root
最开始,我们把root加入队列(root的失败指针显然指向自己),这以后我们每处理一个点,就把它的所有儿子加入队列,直到搞完。
至于为什么这样就搞的定,我们讲下去就知道了。
好了,现在我们有了一棵带失败指针的Trie了,而我的文章也破千字了,接下来,我们就要讲AC自动机是怎么工作的了。
AC自动机是个多串匹配,也就是说会有很多串让你查找,我们先把这些串弄成一棵Trie,再搞一下失败指针,然后我们就可以开始AC自动机了。
一开始,Trie中有一个指针t1指向root,待匹配串(也就是“文章”)中有一个指针t2指向串头。
接下来的操作和KMP很相似:如果t2指向的字母,是Trie树中,t1指向的节点的儿子,那么t2+1,t1改为那个儿子的编号,否则t1顺这当前节点的失败指针向上找,直到t2是t1的一个儿子,或者t1指向根。如果t1路过了一个绿色的点,那么以这个点结尾的单词就算出现过了。或者如果t1所在的点可以顺着失败指针走到一个绿色点,那么以那个绿点结尾的单词就算出现过了。
我们现在回过来讲讲失败指针。实际上找失败指针的过程,是一个自我匹配的过程。
如图,现在假定我们确定了深度小于2(root深度为1)的所有点的失败指针,现在要确定e。这就相当于我们有了这样一颗Trie: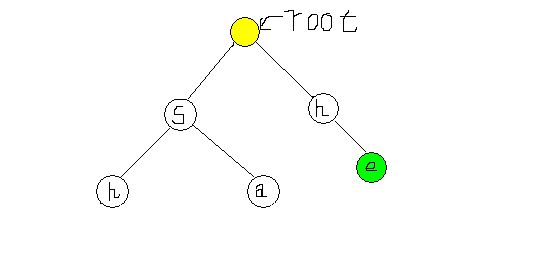
而文章为’she’,要查找’e’在哪里出现。我们接着匹配’say’,那’y’的失败指针就确定了。
好好想想。前面讲的BFS其实就是自我匹配的过程,这也是和KMP很相似的。
好了,就写到这吧,有不明白可以留言或发邮件给我([email protected]),或者在推上fo我(@sdraven)....
DarkRaven原创
做人要厚道,转载请注明出处(否则你将中AC自动机的诅咒,永远A不了题~)
模板:
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define prt(k) cout<<#k"="<<k<<" ";
#define ll long long
const int N=6e5+4;
#include<queue>
struct Trie
{
int next[N][26];
int end[N];
int fail[N];
int L,root;
int idx(char a) {return a-'a';}
int newnode()
{
memset(next[L],-1,sizeof next[L]);
end[L++]=0;
return L-1;
}
Trie() { L=0; root=newnode(); }
void init(){ L=0; root=newnode(); }
void insert(char s[])
{
int n=strlen(s),u=0;
for(int i=0;i<n;i++)
{
int c=idx(s[i]);
int& temp=next[u][c];
if(temp ==-1)
temp=newnode();
u=temp;
}
end[u]++;
}
void build()
{
queue<int> Q;
fail[root]=root;
for(int i=0;i<26;i++)
{
int& temp=next[root][i];
if(temp==-1)
temp=root;
else
{
fail[temp]=root;
Q.push(temp);
}
}
while(!Q.empty())
{
int now=Q.front(); Q.pop();
for(int i=0;i<26;i++)
{
if(next[now][i]==-1)
next[now][i]= next[fail[now]][i];
else
{
fail[next[now][i]]=next[fail[now]][i];
Q.push(next[now][i]);
}
}
}
}
int query(char s[])
{
int n=strlen(s),now=root;
int ret=0;
for(int i=0;i<n;i++)
{
int c=idx(s[i]);
//if(next[u][c]) return -1;
now=next[now][s[i]-'a'];
int temp=now;
while(temp!=root)
{
ret+=end[temp];
end[temp]=0;
temp=fail[temp];
}
}
return ret;
}
};
Trie ac;
char a[199];
int n;
int main()
{
int re; scanf("%d",&re);
char str[1000100];
while(re--)
{
scanf("%d",&n);
ac.init();
for(int i=0;i<n;i++)
{
scanf("%s",str );
ac.insert(str );
}
ac.build();
/** for (int i = 0; i < ac.L; i++)
{
printf("id = %3d ,fail = %3d ,end = %3d, chi = [",i,ac.fail[i],ac.end[i]);
for (int j = 0; j < 4; j++)
printf("%2d ",ac.next[i][j]);
printf("]\n");
} */
scanf("%s",str);
int ans=ac.query(str);
printf("%d\n",ans);
}
}