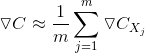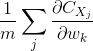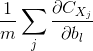梯度下降和随机梯度下降为什么能下降？

首先，我们假设cost function为：

其中，w,b为网络参数，x为训练样本，n为样本数量，y(x)为x的标签，a为网络输出。

我们训练的目的就是让cost function取得最小。为了看起来方便，我们令,则：

        （1）

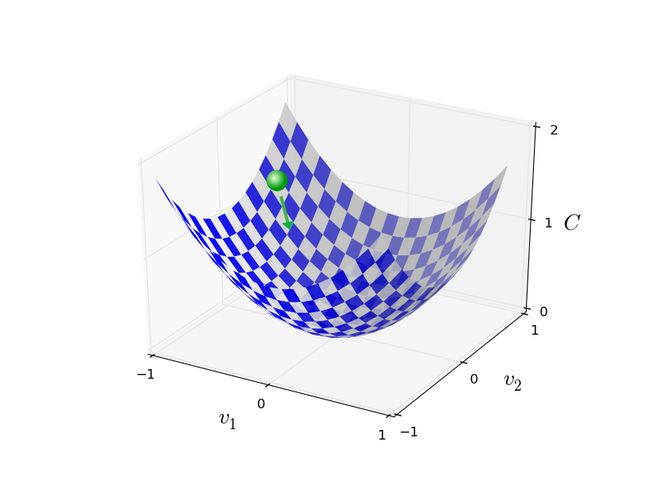
为了方便理解，我们先假设v只有2维,我们要做的就是通过不断调整使得最小。可以通过下图理解，我们为小球选择一个方向，让它往下滚，直到小球滚到“山谷”。

我们令在方向改变，在方向改变，由微积分知识可知：

          （2）

即每次改变，改变后为。为了使不断变小，必须为负。

令，             （3）

                （4）        

(注意这里的上三角和下三角)

  则由（2）、（3）、（4）有： 

                           （5）

我们的目标是让为负，假设：

                              (6)

其中是一个很小的正数(实际上就是我们所说的学习率)，那么，由(5)和(6)：

         (7)

由于，所以,那么，就会一直往减小的方向走，即小球一直往“山谷”滚下去。

我们训练的目的是得到模型参数，由（6）知的更新公式为：

                  (8)

如果将重新看成，那么：

      (9)

                (10)

通过不断计算，更新参数 ，最终得到最小(或足够小)。

实际应用中，应用梯度下降存在很多难题。我们回到cost function：

，我们写成这个形式：

                           （11）

也就是说：

              （12）

其中（12）是对于其中一个训练样本而言的cost funtion。

为了计算，我们要对每一个样本计算，然后，计算平均：

                （13）

因此，当训练样本很多时，计算(13)要很长时间。

由此引出的一个想法叫随机梯度下降(stochastic gradient descent,SGD)，它能加快学习的速度。

这个想法的idea是在训练样本中随机的选择一批样本，然后通过该批样本的各，通过（13）计算。

（此时公式（13）中的n为该批样本的数量）。

为了使随机梯度下降法更有效，SGD随机选择训练样本中的一个小样本集，大小为m，我们记这些样本为：

。这样一批样本称为mini-batch。

假设m足够大，那么的平均大约等于的平均，即：

      （14）

其中第二项的n为训练样本总数，由此可得：

               （15）

那么，w和b的更新公式变为：

    （16）

              （17）

训练完一个mini-batch后，就取另一个mini-batch，直到训练完整个训练集，这就是一个epoch。

有时候，我们可能不知道样本数量n(或者m),我们可以不求平均，直接用和计算。我们看（16）和（17）,去掉m实际上可以看作增大学习率。实际应用中那个效果更好看具体问题而定。

最后，我们总结一下随机梯度下降的过程：

（1）初始化网络参数；

（2）在训练集中取mini-batch，计算，；

（3）由公式（16）和（17）更新参数w，b；

（4）重复（2）-（3），直到C最小(足够小)；

更多知识可以参考这里。