活用各种数据结构——RMQ/树状数组/分桶法和平方分割

对《挑战程序设计竞赛》的一个记录

第三章 出类拔萃——中级篇

上一篇：3.3活用各种数据结构——线段树篇

3.3活用各种数据结构——RMQ/树状数组/分桶法和平方分割

RMQ（区间最值查询）

有一个长度为n的乱序序列，要求求出区间[L,R]内的最大值或最小值（或者有多次询问发生）
（1）普通解法：每次询问遍历一遍数组（效率低，n很小时，可以考虑一下）
（2）ST算法：具体看之前写过的这篇，ST算法可以进行O(1)的查询，但是不能维护值得更改，适合用在需要大量询问，但是不改变值得情况下。
（3）线段树：可以看线段树篇内的习题
（4）树状数组：树状数组见下面详解
用树状数组求区间[L,R]最值时,如果待查区域在[L,R]范围内，则去该区域最值，否则，只取当前位置的数据，索引后减1并重复上述步骤，直至全部查询完

int getMax(int r,int l)
{
    int ans = val[r];
    while(l <= r)
    {
        ans = max(ans,val[r]);
        for(--r; r - l >= lower_bit(r);r -= lower_bit(r))
        {
            ans = max(ans,cnt[r]);
        }
    }
    return ans;
}

（5）平方分割：见下面详解
（6）。。。待补充

树状数组

经常用到YB学长的这份自己整理的资料，觉得挺好，直接贴上来记录一下（侵删，勿转载）

单一更新区间查询
树状数组的原英文表达：Binary Indexed Tree（BIT），直译的意思便是：二进制标记树。这提示我们，树状数组这种数据结构的原理是二进制数。
如果数组A是基础数组，数组C是区间数组。那么，在具体介绍数组C的特点前，先给出如下的树状关系图：

仔细观察上图，容易发现：
数组C[]分别代表的区间为：
C1=A1 [1,1]
C2=C1+A2=A1+A2 [1,2]
C3=A3 [3,3]
C4=C2+C3+A4=A1+A2+A3+A4 [1,4]
C5=A5 [5,5]
C6=C5+A6=A5+A6 [5,6]
C7=A7 [7,7]
C8=C4+C6+C7+A8=A1+A2+A3+A4+A5+A6+A7+A8 [1,8]
C9=A9 [9,9]

也就是说，每个数组Ci，至少包含Ai，同时包含所有满足j+lowest_bit(j)=i的Cj数组。例如C8不仅包含A8，同时还包含了C4,C6,C7。而
410=1002，1002+1002=10002=810
610=1102，1102+102=10002=810
710=1112，1112+12=10002=810
注：lowest_bit(i)表示计算数字i的二进制表示中，从右往左数，第一个1所代表的数字。

利用位运算，
我们容易得到lowest_bit()的快速计算方法：

int lowbit(int x)
{
    return x&-x;
}

于是，在Ai更新时，只需纵向分别更新即可：C[i]，C[i=i+lowest_bit(i)]……直到i>n。
例如在更新A1时候，我们分别更新C1,C2,C4与C8。（这里假设n=9）

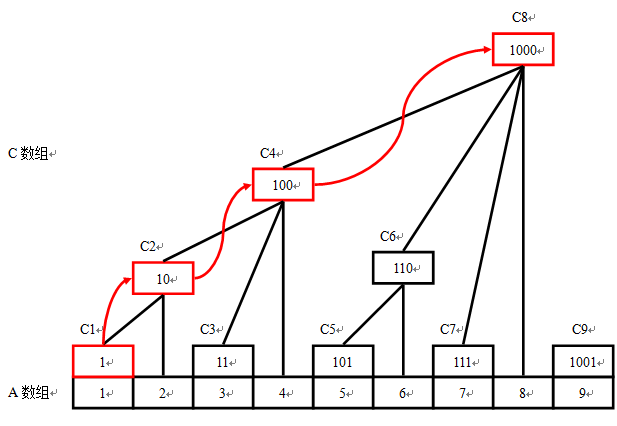
对于更新过程我们可以这样理解：更新所有包含Ai的数组Cj。计算下标j的过程类似于在树形结构中寻找父节点的过程。

实现代码：

void add(int x,int val)
{
    while(x<=n)
    {
        c[x]+=val;
        x+=lowbit(x);
    }
}

对于每个数组Ci，至少包含Ai，同时包含所有满足j+lowest_bit(j)=i的Cj数组。因此，可以得到如下结论：数组Ci代表的区间一定是:[i-lowest_bit(i)+1,i]。（这里略去了该结论的证明过程）
于是，对于A1+A2+……Ai的和，我们只需找到一组能完美覆盖区间[1,i]的数组集合{C[]}即可：C[i]+C[i=i-lowest_bit(i)]+……直到i=0。

例如在查询A1+A2+……A7的值时，我们累加C7+C6+C4

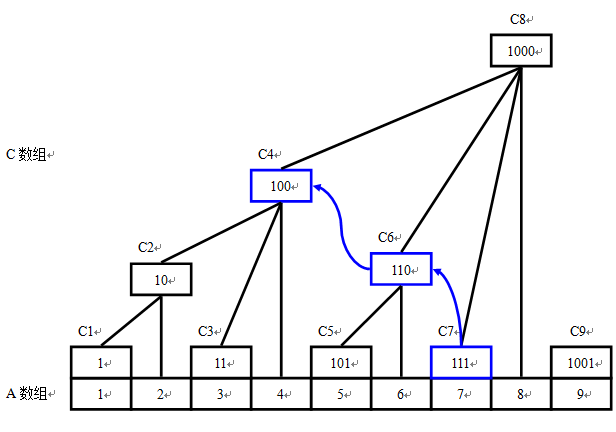
实现代码：

int sum(int x)
{
    int rt=0;
    while(x)
    {
        rt+=c[x];
        x-=lowbit(x);
    }
    return rt;
}

可以看出，树状数组的代码实现非常简洁，极易编码。同时，我们容易计算出树状数组的更新操作的时间复杂度为log(n)，查询操作的时间复杂度同样为log(n)，因此总时间复杂度为log(n)。

题目：

poj 1166 敌兵布阵

#include<iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

int maxn;
int a[55000];
int lowbit(int x)
{
    return x&-x;
}
void Add(int x,int val)
{
    while(x<=maxn)
    {
        a[x]+=val;
        x+=lowbit(x);
    }    
}

void Sub(int x,int val)
{
    while(x<=maxn)
    {
        a[x]-=val;
        x+=lowbit(x);

    }
}
int Sum(int x)
{
    int rt=0;
    while(x)
    {
        rt+=a[x];
        x-=lowbit(x);
    }
    return rt;
}
int main()
{
    int t,text=1;
    scanf("%d",&t);
    while(t--)
    {
        printf("Case %d:\n",text++);
        memset(a,0,sizeof(a));
        int n;
        scanf("%d",&n);
        maxn=n;
        for(int i=1;i<=n;i++)
        {
            int v;
            scanf("%d",&v);
            Add(i,v);
        }   
        char ch[10];
        int x,y;
        while(1)
        {
            scanf("%s",ch);
            if(ch[0]=='E')
                break;
            scanf("%d%d",&x,&y);
            if(ch[0]=='Q')
                printf("%d\n",Sum(y)-Sum(x-1));    
            else if(ch[0]=='A')
                Add(x,y);
            else
                Sub(x,y);
        }
    }
    return 0;
}

hdu1754 I Hate It
hdu1394 Minimum Inversion Number
hdu2795 Billboard
poj2828 Buy Tickets
poj2886 Who Gets the Most Candies?

区间更新单一查询
若需要区间更新，单一查询，那么只要改变数组C的含义即可：数组C表示区间的共同增量，例如，
C1=A1 [1,1]
C2=C1+A2=A1+A2 [1,2]
C3=A3 [3,3]
C4=C2+C3+A4=A1+A2+A3+A4 [1,4]
分别表示区间[1,1]，[1,2]，[3,3]，[1,4]的共同增量，于是在更新区间[1,i]时，我们只需找到一组能完美覆盖区间[1,i]的数组集合{C[]}即可，这刚好对应着之前树状数组的sum操作。于是，我们将sum操作更改为add操作，即

void add(int x, int val)
{
    while(x)
    {
        c[x]+=val;
        x-=lowbit(x);
    }
}

对于区间[s,t]，我们只需执行add(t,val)与add(s-1,-val)即可。

对于单一查询：query(i)，我们只需累加所有包含Ai的数组Cj即可，这对应着之前树状数组的add操作。于是，我们将add操作更改为sum操作，即

int sum(int x)
{
    int rt=0;
    while(x<=n)
    {
        rt+=c[x];
        x+=lowbit(x);
    }
    return rt;
}

题目：
hdu1698 Just a Hook
poj2528 Mayor’s posters
poj3225 Help with Intervals
poj1436 Horizontally Visible Segments
poj2991 Crane
Another LCIS
Bracket Sequence

区间更新区间查询

poj3468 A Simple Problem with Integers
题意：给出n个数和Q个操作，操作如下:
C a b c:将[a, b]区间中的每个数加上c。
Q a b: 计算[a, b ]区间内的数值之和。

这个题目求的是某一区间的数组和，而且要支持批量更新某一区间内元素的值，怎么办呢？实际上，还是可以把该问题转化为求数组的前缀和。

首先，看更新操作update(s, t, d)把区间A[s]……A[t]都增加d，我们引入一个数组delta[i]，表示
A[i]……A[n]的共同增量，n是数组的大小。那么update操作可以转化为：
1）令delta[s] = delta[s] + d，表示将A[s]……A[n]同时增加d，但这样A[t+1]……A[n]就多加了d，所以
2）再令delta[t+1] = delta[t+1] - d，表示将A[t+1]……A[n]同时减d

再看查询操作query(s, t)，求A[s]……A[t]的区间和，转化为求前缀和，设sum[i] = A[1]+ …… +A[i]，
则A[s]+ …… +A[t] = sum[t] - sum[s-1]，

那么前缀和sum[x]又如何求呢？它由两部分组成，一是数组的原始和，二是该区间内的累计增量和， 把数组A的原始值保存在数组org中，并且delta[i]对sum[x]的贡献值为delta[i]*(x+1-i)，
那么
sum[x]=org[1]+……+org[x]+delta[1]∗x+delta[2]∗(x−1)+……+delta[x]∗1=org[1]+……+org[x]+∑(delta[i]∗(x+1−i))=∑(org[i])+(x+1)∗∑(delta[i])−∑(delta[i]∗i)

1 <= i <= x

这其实就是三个数组org[i], delta[i]和delta[i]*i的前缀和，org[i]的前缀和保持不变，事先就可以求出来，delta[i]和delta[i]*i的前缀和是不断变化的，并且每次都是单一更新，所以可以用两个树状数组来维护。

对于delta[i]*i，其实就delta[i]的简单映射关系，于是update操作可以转化为：
1）令delta[s]* s = (delta[s] + d)* s = delta[s]* s+s* d，
2）再令delta[t+1]* (t+1) = delta [t+1]* (t+1) – (t+1)* d，

代码如下：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>

using namespace std;

const int maxn=100010;
typedef long long LL;
int n;
LL delta1[maxn],delta2[maxn],A[maxn];
int lower_bit(int x)
{
    return x&-x;
}
void Init(int x,LL val)
{
    while(x<=n)
    {
        A[x]+=val;
        x+=lower_bit(x);
    }
}
void Add(int x,LL val,int f)
{
    if(f==0)
    {
        while(x<=n)
        {
            delta1[x]+=val;
            x+=lower_bit(x);
        }
    }
    else
    {
        while(x<=n)
        {
            delta2[x]+=val;
            x+=lower_bit(x);
        }
    }

}
LL query(int x,int f)
{
    LL ans=0;
    if(f==0)
    {
        while(x>0)
        {
            ans+=A[x];
            x-=lower_bit(x);
        }
    }
    else if(f==1)
    {
        while(x>0)
        {
            ans+=delta1[x];
            x-=lower_bit(x);
        }

    }
    else
    {
        while(x>0)
        {
            ans+=delta2[x];
            x-=lower_bit(x);
        }
    }
    return ans;
}
int main()
{
    char s[2];
    int m,x,y;
    LL v,z;
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=1;i<=n;i++)
        {
            scanf("%lld",&v);
            Init(i,v);
        }
        while(m--)
        {
            scanf("%s%d%d",s,&x,&y);
            if(s[0]=='Q')
            {
                LL ans=query(y,0)-query(x-1,0)+(y+1)*query(y,1)-(x)*query(x-1,1)-query(y,2)+query(x-1,2);
                printf("%lld\n",ans);
            }
            else
            {
                scanf("%lld",&z);
                Add(x,z,0);
                Add(y+1,-z,0);
                Add(x,z*x,1);
                Add(y+1,-z*(y+1),1);
            }
        }
        memset(delta1,0,sizeof(delta1));
        memset(delta2,0,sizeof(delta2));
        memset(A,0,sizeof(A));
    }
    return 0;
}

分桶法和平方分割

直接贴书上的：

poj 2104 K-th Number
代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <cmath>
#include <vector>
#define sf scanf
#define pf printf

using namespace std;

const int Maxn = 100010;
int val[Maxn],sort_val[Maxn];
int n,m,l,r,k;
vector<int> vec[Maxn];

int binary_sort(int k,int i)
{
    int l = 0, r = vec[i].size() - 1;
    while(l <= r)
    {
        int mid = (l + r) >>1;
        if(vec[i][mid] <= k)
            l = mid + 1;
        else
            r = mid - 1;
    }
    return r + 1;
}
int main()
{
    while(~sf("%d%d",&n,&m))
    {
        int b = ceil(sqrt(n * log(n*1.0)));
        if(n == 1) b = 1;

        for(int i = 0;i < n;i ++)
        {
            sf("%d",&val[i]);
            sort_val[i] = val[i];
            vec[i/b].push_back(val[i]);
        }
        for(int i = 0;i <= (n-1)/b;i++)
            sort(vec[i].begin(),vec[i].end());
        sort(sort_val,sort_val + n);
        while(m --)
        {
            sf("%d%d%d",&l,&r,&k);
            l --;
            r --;
            int x = l / b;
            int y = r / b;
            int L = 0,R = n - 1,mid;
            while(L <= R)
            {
                mid = (L + R) >> 1;
                int key = sort_val[mid];
                int ll = l,rr = r,ans = 0;
                while(ll <= rr && ll < (x + 1) * b)
                    if(val[ll++] <= key) ans ++;

                while(ll <= rr && rr >= y * b)
                    if(val[rr--] <= key) ans ++;

                for(int i = x + 1;i < y;i ++)
                    ans += binary_sort(key,i);
                if(ans < k)
                    L = mid + 1;
                else if(ans >= k)
                    R = mid - 1;

            }
            pf("%d\n",sort_val[L]);
        }
        for(int i = 0;i <= (n-1)/ b;i++)
            vec[i].clear();
    }
    return 0;
}