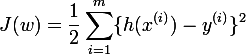最小均方算法（LMS Algorithm）理论及DSP实现

最小均方算法（LMS Algorithm）理论及DSP实现

 LMS算法可认为是机器学习里面最基本也比较有用的算法，神经网络中对参数的学习使用的就是LMS的思想，在通信信号处理领域LMS也非常常见，比如自适应滤波器。

本文主要对LMS（Least Mean Square）算法进行简单的整理，包括内容：

（1）理论上介绍基于LMS的梯度下降算法（包括BACH/STOCHASTIC），给出一个matlab的实现

（2）DSP上的实现，主要使用C语言

1. LMS算法理论

问题引出

因为本人感兴趣的领域为机器学习，因此这里先说明下学习的过程，给定这样一个问题：某地的房价与房地面积和卧室的数量之间成如下表的关系，

Living area (feet2)       #bedrooms          Price (1000$s)
2104                              3                           400
1600                              3                           330
2400                              3                           369
1416                              2                           232
3000                              4                           540

据此，我们要通过分析上面的数据学习出一个模型，用于预测其它情况（比如面积2000,卧室数5）的房价。这就是一个学习问题，更简洁的说，就是一个概率里的回归问题。这里固定几个符号：x表示输入（[Living area，bedrooms]），y表示输出（Price），h表示要学习的模型，m表示输入每个数据维度（这里是2），n表示输入数据的个数（这里是5）。

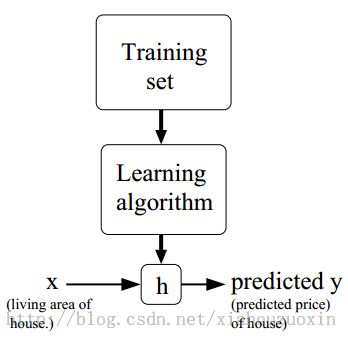
该学习过程的可以描述如下图，

.
h必定与面积和卧室数相关，.这里不考虑复杂的情况，假设模型是线性的（实际其它问题中很可能是其它关系模型，比如exp）
.
.令x1=1，则。这里，我们考虑上面的房价问题，还是将w0忽略。

为了获得h(x)，现在的问题是什么呢？那就是：怎样获得h(x)的w1~w2的值。

我们再对问题进行描述：

已知——上面的数据表格，线性模型（不知道参数）

求解——参数w1~w2

引入一个函数，叫损失函数

就是最小二乘法中计算误差的函数，只是前面添加了1/2，表示什么意思呢？损失函数越小，说明模型与当前已知数据的拟合程度越好，否则越差。因此，求解w1~w2的目标就是求解J(w)最小，这就用到了LMS算法。

LMS算法

LMS算法是一个搜索算法，假设w从某个给定的初始值开始迭代，逐渐使J(W)朝着最小的方向变化，直到达到一个值使J(w)收敛。考虑梯度下降算法（gradient descent algorithm），它通过给定的w值快速的执行如下的更新操作：

其中为学习率（Learning rate）。

要对w更新，首先需要完成上面的求导，求导的结果参见下面的算法流程。

对一个单一的训练实例j，

按照上述的更新方法，对多个实例的更新规则为

Repeat until convergence {

        for every j, exec

                  

}

这种更新的梯度下降方法称为batch gradient descent。还有一种更新的方式：采用随机的样本数据实例，如下

Repeat until convergence {

        for every j, exec

                  

}

这种方法称为stochastic gradient descent (或者incremental gradient descent)。

两种方法的明显区别是batch的训练时间要比stochastic常，但效果可能更好。实际问题中，因为我们只需要找到一个接近使J(w)最小的值即可，因此stochastic更常用。

说了这么久，LMS到底能用来干嘛，其实上面已经很清楚了：参数训练中的求极值。

在matlab上对stochastic gradient descent 的实现如下：

 function [test_targets, a, updates] = LMS(train_patterns, train_targets, test_patterns, params)

 % Classify using the least means square algorithm
 % Inputs:
 %   train_patterns  - Train patterns
 %   train_targets   - Train targets
 %   test_patterns   - Test  patterns
 %   param           - [Maximum iteration Theta (Convergence criterion), Convergence rate]
 %
 % Outputs
 %   test_targets    - Predicted targets
 %   a               - Weights vector
 %   updates         - Updates throughout the learning iterations
 %
 % NOTE: Suitable for only two classes
 %

 [c, n]                  = size(train_patterns);
 [Max_iter, theta, eta]  = process_params(params);

 y               = [train_patterns ; ones(1,n)];
 train_zero      = find(train_targets == 0);

 %Preprocessing
 processed_patterns               = y;
 processed_patterns(:,train_zero) = -processed_patterns(:,train_zero);
 b                                = 2*train_targets - 1;

 %Initial weights
 a               = sum(processed_patterns')';
 iter            = 1;
 k               = 0;
 update          = 1e3;
 updates         = 1e3;

 while ((sum(abs(update)) > theta) & (iter < Max_iter))
     iter = iter + 1;

     %k <- (k+1) mod n
     k = mod(k+1,n);
     if (k == 0),
         k = n;
     end

     % a <- a + eta*(b-a'*Yk)*Yk'
     update  = eta*(b(k) - a'*y(:,k))*y(:,k);
     a       = a + update;

     updates(iter) = sum(abs(update));
 end

 if (iter == Max_iter),
     disp(['Maximum iteration (' num2str(Max_iter) ') reached']);
 else
     disp(['Did ' num2str(iter) ' iterations'])
 end

 %Classify the test patterns
 test_targets = a'*[test_patterns; ones(1, size(test_patterns,2))];

 test_targets = test_targets > 0;

2. 基于LMS的梯度下降算法在DSP上的实现

下面是我在DSP6713上使用软件仿真实现的LMS算法，

 /*
  * zx_lms.h
  *
  *  Created on: 2013-8-4
  *      Author: monkeyzx
  */

 #ifndef ZX_LMS_H_
 #define ZX_LMS_H_

 /*
  * methods for @lms_st.method
  */
 #define STOCHASTIC           (0x01)     /* 随机梯度下降 */
 #define BATCH                (0x02)     /* BATCH梯度下降 */

 struct lms_st {
     short method;       /* 0/1 */
     double *x;          /* features, x0,...,x[n-1] */
     int n;              /* dimension of features */
     double *y;          /* given output, y0,..,y[m-1] */
     int m;              /* number of data set */
     double *weight;     /* weighs that want to train by using LMS, w0,w1,..,w[n-1] */
     double lrate;       /* learning rate */
     double threshhold;  /* if error < threshold, stop iteration */
     int max_iter;       /* if iter numbers > max_iter, stop iteration,
                            if max_iter<0, then max_iter is unused */
 };

 extern void zx_lms(void);

 #endif /* ZX_LMS_H_ */

 /*
  * zx_lms.c
  * Least Mean Squares Algorithm
  *  Created on: 2013-8-4
  *      Author: monkeyzx
  */
 #include "zx_lms.h"
 #include "config.h"
 #include <stdio.h>
 #include <stdlib.h>

 static double init_y[] = {4.00,3.30,3.69,2.32};
 static double init_x[] = {
         2.104,3,
         1.600,3,
         2.400,3,
         3.000,4
 };
 static double weight[2] = {0.1, 0.1};

 /*
  * Least Mean Square Algorithm
  * return value @error when stop iteration
  * use @lms_prob->method to choose a method.
  */
 double lms(struct lms_st *lms_prob)
 {
     double err;
     double error;
     int i = 0;
     int j = 0;
     int iter = 0;
     static double *h = 0;       /* 加static,防止栈溢出*/

     h = (double *)malloc(sizeof(double) * lms_prob->m);
     if (!h) {
         return -1;
     }
     do {
         error = 0;

         if (lms_prob->method != STOCHASTIC) {
             i = 0;
         } else {
             /* i=(i+1) mod m */
             i = i + 1;
             if (i >= lms_prob->m) {
                 i = 0;
             }
         }

         for ( ; i<lms_prob->m; i++) {
             h[i] = 0;
             for (j=0; j<lms_prob->n; j++) {
                 h[i] += lms_prob->weight[j] * lms_prob->x[i*lms_prob->n+j]; /* h(x) */
             }
             if (lms_prob->method == STOCHASTIC) break;   /* handle STOCHASTIC */
         }

         for (j=0; j<lms_prob->n; j++) {
             if (lms_prob->method != STOCHASTIC) {
                 i = 0;
             }
             for ( ; i<lms_prob->m; i++) {
                 err = lms_prob->lrate
                         * (lms_prob->y[i] - h[i]) * lms_prob->x[i*lms_prob->n+j];
                 lms_prob->weight[j] += err;            /* Update weights */
                 error += ABS(err);
                 if (lms_prob->method == STOCHASTIC) break; /* handle STOCHASTIC */
             }
         }

         iter = iter + 1;
         if ((lms_prob->max_iter > 0) && ((iter > lms_prob->max_iter))) {
             break;
         }
     } while (error >= lms_prob->threshhold);

     free(h);

     return error;
 }

 #define DEBUG
 void zx_lms(void)
 {
     int i = 0;
     double error = 0;
     struct lms_st lms_prob;

     lms_prob.lrate = 0.01;
     lms_prob.m = 4;
     lms_prob.n = 2;
     lms_prob.weight = weight;
     lms_prob.threshhold = 0.2;
     lms_prob.max_iter = 1000;
     lms_prob.x = init_x;
     lms_prob.y = init_y;
 //  lms_prob.method = STOCHASTIC;
     lms_prob.method = BATCH;

 //  error = lms(init_x, 2, init_y, 4, weight, 0.01, 0.1, 1000);
     error = lms(&lms_prob);

 #ifdef DEBUG
     for (i=0; i<sizeof(weight)/sizeof(weight[0]); i++) {
         printf("%f\n", weight[i]);
     }
     printf("error:%f\n", error);
 #endif
 }

输入、输出、初始权值为

static double init_y[] = {4.00,3.30,3.69,2.32};
static double init_x[] = {        /* 用一维数组保存 */
2.104, 3,
1.600, 3,
2.400, 3,
3.000, 4
};
static double weight[2] = {0.1, 0.1};

main函数中只需要调用zx_lms()就可以运行了，本文对两种梯度下降方法做了个简单对比，

max_iter=1000	w1	w2	error	CPU Cycles
batch	-0.6207369	1.419737	0.20947	2181500
stochastic	0.145440	0.185220	0.130640	995

需要说明的是：batch算法是达到最大迭代次数1000退出的，而stochastic是收敛退出的，因此这里batch算法应该没有对数据做到较好的拟合。stochastic算法则在时钟周期上只有995，远比batch更有时间上的优势。

注：这里的error没有太大的可比性，因为batch的error针对的整体数据集的error，而stochastic 的error是针对一个随机的数据实例。

LMS有个很重要的问题：收敛。开始时可以根据给定数据集设置w值，使h(x)尽可能与接近y，如果不确定可以将w设置小一点。

这里顺便记录下在调试过程中遇到的一个问题：在程序运行时发现有变量的值为1.#QNAN。

解决：QNAN是Quiet Not a Number简写，是常见的浮点溢出错误，在网上找到了解释

A QNaN is a NaN with the most significant fraction bit set. QNaN’s propagate freely through most arithmetic operations. These values pop out of an operation when the result is not mathematically defined.

在开始调试过程中因为迭代没有收敛，发散使得w和error等值逐渐累积，超过了浮点数的范围，从而出现上面的错误，通过修改使程序收敛后上面的问题自然而然解决了。

参考：

[1] Andrew Ng的机器学习课程

[2] Richard O.Duda 等，《模式分类》