【后缀自动机】【SAM】【自动机】【数据结构】后缀自动机理解(入门)
引入
来吧后缀自动机 我们先来看一看后缀数组可以干一些什么事情
1.可以查看当前后缀在所有后缀的排名
2.可以看最大的相同子串
但是缺点呢却也非常的明显——显然这tm是个静态的。。。。
于是只好另辟蹊径——后缀自动机
我们来看看后缀自动机可以干一些什么:
1.可以看子串的相同子串
2.动态插入新的节点
3.空间开销小
…….
擦既然这么多优点为什么不用?
样例
我们同样以下面的例子来介绍后缀自动机我们看一看下面使用abc串构建的简单的后缀自动机
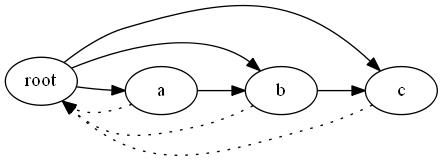
呵呵我承认是有点扭曲,凑合着看一看吧
我们可以发现这个图有以下的性质:
1.首先每一个节点到根的路径上的所有字符构成的都是原串的子串
2.c和根相连接,同时根(空集)和c到根的路径上的任意一个点都可以作为一个后缀
3.我们可以发现虚线连接的边都是当前后缀(到根的路径)上的最长的后缀的后缀(这个性质非常重要有助于我们后面做很多的题目)
这里我们讲一下这样的定义我们令
Len(i)表示从根到i节点的所有字符串中最长的那一个字符串
Ch(i,c)表示i的儿子字符c的那个节点
Fail(i)表示i节点连接的虚线边
概念
这里我们再讲一个概念:我们可以发现任意一个节点可以构成许多个子串比如:上面的图中b节点就同时代表了a和ab两个子串,同时我们可以发现在字符串中a和ab的结尾位置是相同的,所以我们认为每个节点也表示了一个终点位置的集合 重点:且这些同一个节点的字符串的结束位置全部相同,如果这个时候a在字符串的另一个位置也出现的话,那么我们就不能这样表示了。
结论一
我们可以假设当前节点表示的字符串最长为R, 最短为L那么我们可以发现因为L必定为R的后缀那么同时又有L最短,那么如果有mid处于L和R的长度之间,那么我们一定有mid的出现次数相同且L为mid的后缀那么mid必定在当前节点表示的子串中,那么我们可以发现任意一个节点表示的字符串长度是有一个范围的连续区间组成的
结论二
我们来观察一下上面的图片发现一下虚线到底维护了一个怎样的性质?
我们可以发现虚线指向的是后缀相同但是又无法满足每一个字符串的位置都相同的上一个位置(当然这个结论是我YY出来的后面多看看就明白了)为什么要维护这样的一个性质呢?通过观察我们可以发现结论1,当前是满足的,同时为了满足自动机,我们需要使用Fail的边来(虚线的边)在新建的过程中减少空间(比如下面的样例中的)插入一个节点至多只新建了两个节点这样空间就可以开(2N)就足够了
结论三
只有最后的c节点(last)节点和他的虚线连接的边可以作为当前整个已经添加节点的字符串的后缀(根据上面的两个结论可以很容易得到当前的结论)
实际操作
其实知道了这几个结论我们就可以开始做题了,我们先举一个例子看看如果构建自动机:abaa首先第一步是一个空串root

然后我们引入a,将上一个节点以及每一个上一个节点的虚线构成的路径上的所有节点都向当前节点连接一条边
同时我们发现根据结论二我们有a向root 连接一条虚线边,此时最后的节点变成了a(1号节点)
呵呵
然后添加b节点, b成为了last

此时我们再次添加 a2 节点,我们会发现此时b作为last的时候他的虚线构成的边上的root的a这个已经被占用了呢。。。。此时我们发现Len(a)=Len(root)+1的这就表示这个a已经成为了root最长的串+1长的串了,那么我们直接令Fail( a2 )=a

但是如果Len(a)!=Len(root)+1会发生什么呢,那么久代表着a节点还有其他的限制,当前的这个地方如果a再作为Fail( a2 )就会出现并不存在在当前串中的串,那么就会打破性质1(这个内容下面还会讲到)
接着我们继续添加 a3 同理得到
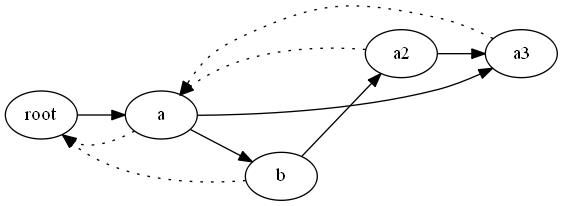
这样的图形,下面我们来说明上面的冲突问题
冲突与完善
就继续使用上面的例子我们现在匹配abaaa那么此时我们还需要添加一个a到上图中去,显然第一步:将 a3 连接 a4 然后我们跳转到a发现a已经有了 a3 这个儿子了那么此时我们判断L( a3 )是否等于Len(a)+1显然并不,那么我们采取以下的方法。首先我们新建一个 a33 并且复制 a3 的所有信息可以得到如下的图
为了维护上面的结论一成立我们沿着a的Fail边走将所有Fail边上原来连接够a3的边全部链接给a33此时将Len(a33)设置为Len(a)+1那么显然我们的Fail(a4)就可以连接给a33了,同时我们为了维护结论一,将Fail(a3)设置为a33,这样就保证了所有性质的维护我们可以得到如下的图
好吧,虽然图有点丑但是还是不妨碍大家求知的决心
代码
void Insert(int c){
node *np = ++ecnt, *p = last;
np->len = last->len+1;
last = np;
while(p&&!p->ch[c])
p->ch[c]=np, p=p->fail;
if(!p)
np->fail = root;
else{
node *q = p->ch[c];
if(p->len+1 == q->len){
np->fail = q;
}else{
node *nq = ++ecnt;
*nq = *q;
nq->len = p->len+1;
np->fail = nq;
q->fail = nq;
while(p&&p->ch[c]==q)
p->ch[c]=nq, p=p->fail;
}
}
}相关习题
[SPOJ LCS]Longest Common Substring: 题解
[SPOJ LCS2]Longest Common Substring II:题解
更多题目
感谢
感谢您阅读本篇博客,如果有什么写的不好的地方求留下评论(谢谢)