【HDOJ】 Picture (离散化+线段树)

【HDOJ】 Picture (离散化+线段树)

Picture

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3898    Accepted Submission(s): 1979

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.



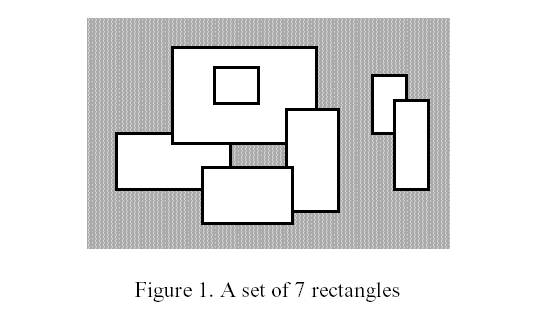
The corresponding boundary is the whole set of line segments drawn in Figure 2.



The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

   
   
   
   

    
    
    
    7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    228
   
   
   
   

 

Source

IOI 1998

 

线段树都写不来了。。简直了……
我已经是半个废人了……

关于这题的题解博客满天飞……不过算是自立门户吧= =写了个不一样的线段树，就叫乱七八糟树好了……///
不知道有没有跟我的写法一样的，也没看过别的大犇的写法。。。。

做法跟网上的一样，每个矩形拆分成两个边，左入右出然后按照x从小到大排序 x相同的 入边在前！！！！！
例子：
2
0 0 1 1
0 1 1 2
正解为6

对于y进行离散化。线段树中存放离散化后的下标，每个下标表示从该y到下一个y这条线段(区间

接下来，我对线段树的处理如下:
遍历每条边，如果是入边，在区间[y1,y2]+1 否则-1
如果加之前区间[y1,y2]为0 表示是在空白处加上这条边 那么就要统计上y2-y1
如果减之前区间[y1,y2]为1 表示减去这条边后会[y1,y2]会变为空白，那么就要统计上y2-y1

这是对于纵边的统计，说起来比较简单，但在线段树中实现出来就略繁琐。。反正我是这样……

对于横边，当遍历到某个边，这个边的x比前一条边大，换句话说，也就是从前一条边到这条边会向右拉伸一段距离，而这段距离就是横边的长度
那么横边的数量，其实也就是加上这条新边之前，连续的y区间 ×2

当然，先理解……实现起来，，，。。。。我卡了近五天(此处表情为微笑 :>)

#include <iostream>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <list>
#include <algorithm>
#include <map>
#include <set>
#define LL long long
#define Pr pair<int,int>
#define fread() freopen("in.in","r",stdin)
#define fwrite() freopen("out.out","w",stdout)

using namespace std;
const int INF = 0x3f3f3f3f;
const int msz = 10000;
const int mod = 1e9+7;
const double eps = 1e-8;

struct Rectangle
{
	int x,y1,y2;
	int ad;
	bool operator <(const struct Rectangle a)const
	{
		return x == a.x? ad > a.ad: x < a.x;
	}
};

//存放矩形拆出的边
Rectangle rec[11111];
//线段树 如果为0表示当前区间为空白 如果为-1表示当前区间有空白也有线段，需要继续向下遍历 如果大于0表示当前区间的线段数量
int bit[666666];
//纵坐标离散化
int rey[11111];
//统计连续区间数量
int part;
//纵坐标离散化后总编号 ans:答案
int tp,ans;

//root:树根 l:区间左边界 r:区间右边界 ll:纵坐标左边界 rr:纵坐标右边界 d:增量
void update(int root,int l,int r,int ll,int rr,int d)
{
	if(ll == rr) return;
	if(rey[l] == ll && rey[r+1] == rr && bit[root] != -1)
	{
		if((bit[root] == 0 && d == 1)||(bit[root]+d == 0 && d == -1)) ans += rr-ll;
			//printf("add:%d-%d\n",ll,rr);
			
		bit[root] += d;
		return;
	}

	int mid = (l+r)>>1;

	//如果当前区间不为-1 需要更新下去
	if(bit[root] != -1)	bit[root<<1] = bit[root<<1|1] = bit[root];

	if(rey[mid+1] >= rr) update(root<<1,l,mid,ll,rr,d);
	else if(rey[mid+1] <= ll) update(root<<1|1,mid+1,r,ll,rr,d);
	else
	{
		update(root<<1,l,mid,ll,rey[mid+1],d);
		update(root<<1|1,mid+1,r,rey[mid+1],rr,d);
	}

	if(bit[root<<1] == bit[root<<1|1] && bit[root<<1] == 0) bit[root] = 0;
	else if(bit[root<<1] == bit[root<<1|1]) bit[root] = bit[root<<1];
	else bit[root] = -1;
}

int lf,rf;
void geth(int root,int l,int r)
{
	if(bit[root] != -1)
	{
		if(root == 1 && bit[root]) part++;
		lf = bit[root];
		rf = bit[root];
		return;
	}
	int l1,r1,l2,r2;
	int mid = (l+r)>>1;
	geth(root<<1,l,mid);
	l1 = lf,r1 = rf;
	geth(root<<1|1,mid+1,r);
	l2 = lf,r2 = rf;

	if(root == 1 && l1 > 0) part++;
	if(r1 == 0 && l2 > 0) part++;

	lf = l1;
	rf = r2;
}

int main()
{
	//fread();
	//fwrite();

	int n;
	while(~scanf("%d",&n))
	{
		int tmp = 0;
		for(int i = 0; i < n; ++i)
		{
			scanf("%d%d%d%d",&rec[tmp].x,&rec[tmp].y1,&rec[tmp+1].x,&rec[tmp].y2);
			rec[tmp].ad = 1;
			rey[tmp] = rec[tmp].y1;
			tmp++;

			rec[tmp].ad = -1;
			rec[tmp].y1 = rec[tmp-1].y1;
			rec[tmp].y2 = rec[tmp-1].y2;

			rey[tmp] = rec[tmp].y2;
			tmp++;
		}

		sort(rey,rey+tmp);
		sort(rec,rec+tmp);

		int tp = 0;
		for(int i = 0; i < tmp; ++i)
		{
			if(i == 0 || rey[i] != rey[tp-1]) rey[tp++] = rey[i];
		}

		ans = 0;
//		for(int i = 0; i < tp; ++i)
//			printf("%d ",rey[i]);
//		puts("");

		memset(bit,0,sizeof(bit));
		for(int i = 0; i < tmp; ++i)
		{
			//printf("time:%d %d %d\n",i,rec[i].y1,rec[i].y2);
			if(i != 0 && rec[i].x != rec[i-1].x) 
			{
				part = 0;
				geth(1,0,tp-2);
				ans += part*2*(rec[i].x-rec[i-1].x);
				//printf("%d\n",ans);
			}
			update(1,0,tp-2,rec[i].y1,rec[i].y2,rec[i].ad);
		}
		printf("%d\n",ans);
	}

	return 0;
}