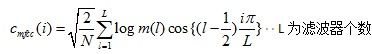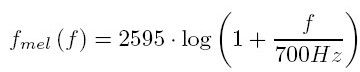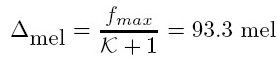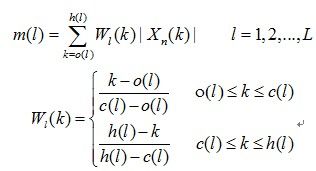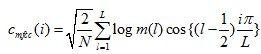MFCC特征提取详细计算过程
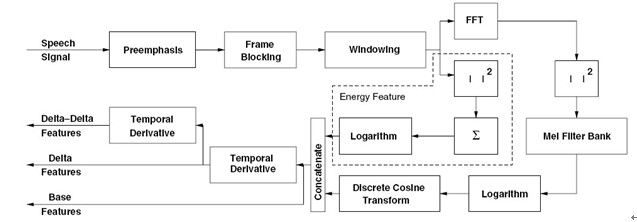
一、MFCC计算总体流程
1.信号的预处理,包括预加重(Preemphasis),分帧(Frame Blocking),加窗(Windowing)。假设语音信号的采样频率fs=8KHz.由于语音信号在10-30ms认为是稳定的,则可设置帧长为80~240点。帧移可以设置为帧长的1/2.
预加重处理其实是一个高通滤波器,该高通滤波顺的传递函数为:
其中的取值为0.97,该高通滤波器作用是滤去低频,使语音信号的高频特性更加突现。
由于语音信号只在较短的时间内呈现平稳性(一般认为 10-30ms ),(项目中每帧是24ms,48K pcm每ms 48个采样点,24 * 48 = 1152)因此将语音信号划分为一个一个的短时段即一帧。同时为避免丢失语音信号的动态信息,相邻帧之间要有一段重叠区域,重叠区域一段为帧长的 1/2 或 1/3 。然后再将每帧乘上窗函数,以增加每帧左端和右端的连续性。2.对每一帧进行FFT变换,求频谱,进而求得幅度谱。
对分帧加窗后的各帧信号进行FFT变换得到各帧的频谱。并对语音信号的频谱取模平方得到语音信号的功率谱。
3.对幅度谱加Mel滤波器组(Mel滤波器组设计问题)。
4.对所有的滤波器输出做对数运算(Logarlithm),再进一步做离散余弦变换DCT可得MFCC。做对数运算是为了
调到分贝(dB)域(也是为了模拟人耳),DCT是为了压缩。只用20个coefficients表示,阔以重建mfcc(dB)。
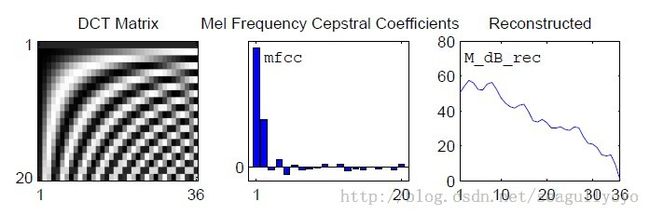
图1:DCT压缩前的MFCC in dB
图2为DCT系数矩阵、DCT压缩后、DCT重建后的mfcc_dB
流程图如下所示:
二、实际频率与Mel频率的转换
Mel频率与实际频率的具体关系如下:
人耳的听觉特性与Mel频率的增长一致。与实际频率在1000Hz以下呈现线性分布,1000Hz以上呈现对数增长。
在 Mel 频率轴上配置 K 个通道的三角形滤波器组, K 的个数由信号的截止频率决定。
设计的过程如下:
假设语音信号的采样频率,帧长N=256,滤波器个数K=22
由此可得语音信号的最大频率为:(奈奎斯特)
根据下面的公式:
可以求得出最大的Mel频率为:![]()
由于在Mel刻度范围内,各个三角滤波器的中心频率是相等间隔的线性分布。由此,可以计算两个相邻三角滤波器的中心频率的间距为:
因此,各三角形滤波器在mel刻度上的中心频率可以表示为:
Mel(f(m))-Mel(f(m-1))=Mel(f(m+1))-Mel(f(m))
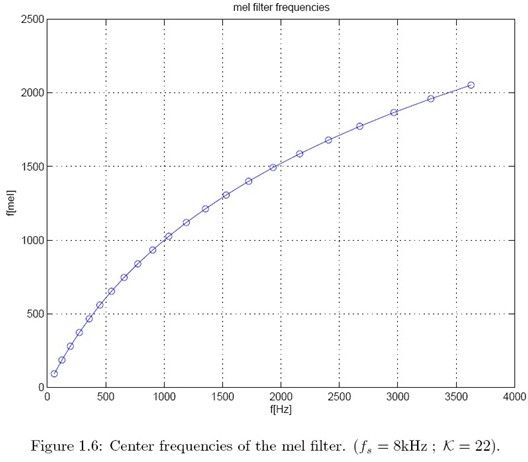
由上面的中心频率可以计算出对应的线性刻度上的频率。如下图所示:可以看出在y轴,mel中心频率是均匀分布的,而在x轴,随着频率
增大,f中心频率间隔越来越大。
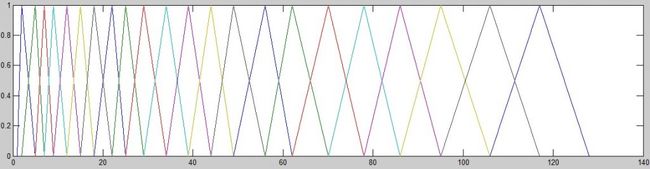
下面采用Matlab设计Mel三角形滤波器如下:
//获取Mel三角滤波器的参数
fs为采样频率,filterNum为三角滤波器的个数
maxMelFreq = freq2mel(fs/2); %将线性频率转化为mel频率,得到最大的Mel频率
sideWidth=maxMelFreq/(filterNum+1);%求频带宽带,即Mel滤波器宽度
index=0:filterNum-1;%滤波器的中心
filterBankPrm=floor(mel2freq([index;index+1;index+2]*sideWidth)/fs*frameSize)+1;
filterBankPrm(end, end)= frameSize/2;
得到如下的三角形滤波器,横坐标对应于FFT中的点的下标:
注:这里选择的帧长为256点,然后FFT的点数也为256,由于是对称的,所以只取前面一半的点计算频谱。然后加入到三角滤波器中。
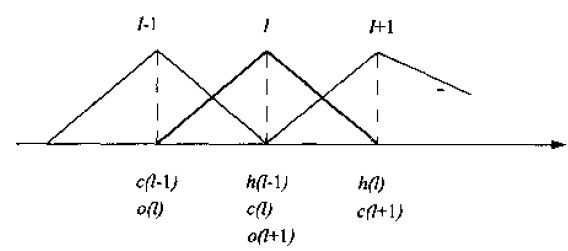
每一个三角形滤波器的中心频率c(l) 在Mel频率轴上等间隔分布。设o(l),c(l),h(l) 分别是第l 个三角形滤波器的下限,中心,和上限频率,则相邻三角形滤波器之间的下限,中心,上限频率的关系如下:c(l)=h(l-1)=o(l+1)
根据语音信号幅度谱![]() 求每个三角形滤波器的输出。
求每个三角形滤波器的输出。
对所有的滤波器输出做对数运算,再进一步做离散余弦变换(DCT)即可得到MFCC。
由上公式可知,MFCC特征参数的长度与滤波器的个数无关。只与DCT有关。
% === 对幅度谱进行三角滤波过程
function tbfCoef = triBandFilter(fftMag, P, filterBankParam)
fstart=filterBankParam(1,:); %fftMag一帧数据的幅度谱
fcenter=filterBankParam(2,:);%滤波器的中心点,每列代表一个滤波器的中心频率
fstop=filterBankParam(3,:);
% Triangular bandpass filter.
for i=1:P %滤波器个数
for j = fstart(i):fcenter(i), %第i个滤波器起始频谱点和中心频谱点的输出
filtmag(j) = (j-fstart(i))/(fcenter(i)-fstart(i));
end
for j = fcenter(i)+1:fstop(i),
filtmag(j) = 1-(j-fcenter(i))/(fstop(i)-fcenter(i));
end
tbfCoef(i) = sum(fftMag(fstart(i):fstop(i)).*filtmag(fstart(i):fstop(i))'); %第i个滤波器的输出
end
tbfCoef=log(eps+tbfCoef.^2); %求得每个滤波器的对数输出,有多少个滤波器就有多少个输出,对应为每一帧