十大经典数据挖掘算法之C4.5算法
C4.5是一系列用在机器学习和数据挖掘的分类问题中的算法。它的目标是监督学习:给定一个数据集,其中的每一个元组都能用一组属性值来描述,每一个元组属于一个互斥的类别中的某一类。C4.5的目标是通过学习,找到一个从属性值到类别的映射关系,并且这个映射能用于对新的类别未知的实体进行分类。C4.5由J.Ross Quinlan在ID3的基础上提出的。ID3算法用来构造决策树。决策树是一种类似流程图的树结构,其中每个内部节点(非树叶节点)表示在一个属性上的测试,每个分枝代表一个测试输出,而每个树叶节点存放一个类标号。一旦建立好了决策树,对于一个未给定类标号的元组,跟踪一条有根节点到叶节点的路径,该叶节点就存放着该元组的预测。决策树的优势在于不需要任何领域知识或参数设置,适合于探测性的知识发现。
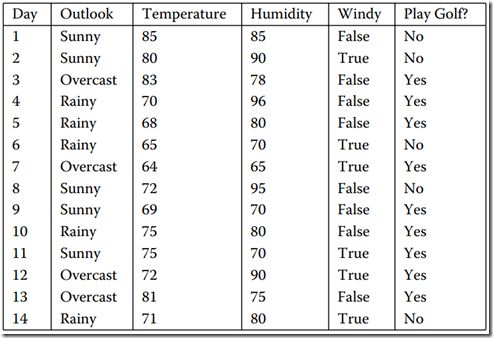
如图1所示的数据集,它表示的是天气情况与去不去打高尔夫球之间的关系。
图1 数据集
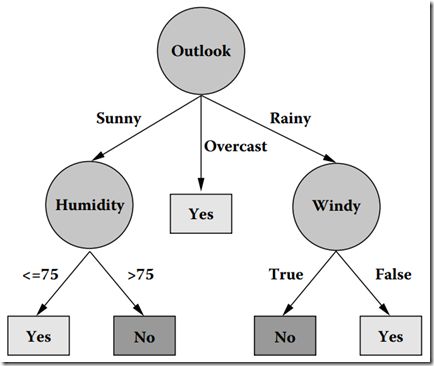
下图2所示,就是一棵由C4.5算法对上面数据集产生的决策树
图2 在数据集上通过C4.5生成的决策树
通过上图可以看到,通过四个属性重要性的不同,就可以划分出不同的分支,我们可能有疑问,一个元组本身有很多属性,我们怎么知道首先要对哪个属性进行判断,接下来要对哪个属性进行判断?换句话说,在图2中,我们怎么知道第一个要测试的属性是Outlook,而不是Windy?其实,能回答这些问题的一个概念就是属性选择度量。
属性选择度量
属性选择度量又称分裂规则,因为它们决定给定节点上的元组如何分裂。属性选择度量提供了每个属性描述给定训练元组的秩评定,具有最好度量得分的属性被选作给定元组的分裂属性。目前比较流行的属性选择度量有--信息增益、增益率和Gini指标。C4.5使用信息增益或者信息增益率作为属性选择度量。(离散属性值使用信息增益,连续属性值使用信息增益率,实际应用中通常对连续属性值进行离散化)
下面分别介绍每种属性选择度量的定义,先做一些假设,设D是类标记元组训练集,类标号属性具有m个不同值,m个不同类Ci(i=1,2,…,m),CiD是D中Ci类的元组的集合,|D|和|CiD|分别是D和CiD中的元组个数。
(1)信息增益
信息增益实际上是ID3算法中用来进行属性选择度量的。它选择具有最高信息增益的属性来作为节点N的分裂属性。该属性使结果划分中的元组分类所需信息量最小。对D中的元组分类所需的期望信息为下式:
Info(D)又称为熵。
现在假定按照属性A划分D中的元组,且属性A将D划分成v个不同的类。在该划分之后,为了得到准确的分类还需要的信息由下面的式子度量:
信息增益定义为原来的信息需求(即仅基于类比例)与新需求(即对A划分之后得到的)之间的差,即
![]() (3)
(3)
我想很多人看到这个地方都觉得不是很好理解,所以我自己的研究了文献中关于这一块的描述,也对比了上面的三个公式,下面说说我自己的理解。
一般说来,对于一个具有多个属性的元组,用一个属性就将它们完全分开几乎不可能,否则的话,决策树的深度就只能是2了。从这里可以看出,一旦我们选择一个属性A,假设将元组分成了两个部分A1和A2,由于A1和A2还可以用其它属性接着再分,所以又引出一个新的问题:接下来我们要选择哪个属性来分类?对D中元组分类所需的期望信息是Info(D) ,那么同理,当我们通过A将D划分成v个子集Dj(j=1,2,…,v)之后,我们要对Dj的元组进行分类,需要的期望信息就是Info(Dj),而一共有v个类,所以对v个集合再分类,需要的信息就是公式(2)了。由此可知,如果公式(2)越小,是不是意味着我们接下来对A分出来的几个集合再进行分类所需要的信息就越小?而对于给定的训练集,实际上Info(D)已经固定了,所以选择信息增益最大的属性作为分裂点。
但是,使用信息增益的话其实是有一个缺点,那就是它偏向于具有大量值的属性。什么意思呢?就是说在训练集中,某个属性所取的不同值的个数越多,那么越有可能拿它来作为分裂属性。例如一个训练集中有10个元组,对于某一个属相A,它分别取1-10这十个数,如果对A进行分裂将会分成10个类,那么对于每一个类Info(Dj)=0,从而式(2)为0,该属性划分所得到的信息增益(3)最大,但是很显然,这种划分没有意义。
(2)信息增益率
正是基于此,ID3后面的C4.5采用了信息增益率这样一个概念。信息增益率使用“分裂信息”值将信息增益规范化。分类信息类似于Info(D),定义如下:
这个值表示通过将训练数据集D划分成对应于属性A测试的v个输出的v个划分产生的信息。信息增益率定义:
选择具有最大增益率的属性作为分裂属性。
(3)Gini指标
Gini指标在CART中使用。Gini指标度量数据划分或训练元组集D的不纯度,定义为:
(6)
下面以C4.5的信息增益和信息增益率为例,介绍决策树生成过程,上面的训练集有4个属性,即属性集合A={OUTLOOK, TEMPERATURE, HUMIDITY, WINDY};而类标签有2个,即类标签集合C={Yes, No},分别表示适合打高尔夫球和不适合打高尔夫球,其实是一个二分类问题。
我们计算信息增益,这里直接列出来,如下所示:数据集D包含14个训练样本,其中属于类别“Yes”的有9个,属于类别“No”的有5个,则计算其信息熵:
1 |
Info(D) = -9/14 * log2(9/14) - 5/14 * log2(5/14) = 0.940 |
下面对属性集中每个属性分别计算信息熵,如下所示:
1 |
Info(OUTLOOK) = 5/14 * [- 2/5 * log2(2/5) – 3/5 * log2(3/5)] + 4/14 * [ - 4/4 * log2(4/4) - 0/4 * log2(0/4)] + 5/14 * [ - 3/5 * log2(3/5) – 2/5 * log2(2/5)] = 0.694 |
2 |
Info(TEMPERATURE) = 4/14 * [- 2/4 * log2(2/4) – 2/4 * log2(2/4)] + 6/14 * [ - 4/6 * log2(4/6) - 2/6 * log2(2/6)] + 4/14 * [ - 3/4 * log2(3/4) – 1/4 * log2(1/4)] = 0.911 |
3 |
Info(HUMIDITY) = 7/14 * [- 3/7 * log2(3/7) – 4/7 * log2(4/7)] + 7/14 * [ - 6/7 * log2(6/7) - 1/7 * log2(1/7)] = 0.789 |
4 |
Info(WINDY) = 6/14 * [- 3/6 * log2(3/6) – 3/6 * log2(3/6)] + 8/14 * [ - 6/8 * log2(6/8) - 2/8 * log2(2/8)] = 0.892 |
根据上面的数据,我们可以计算选择第一个根结点所依赖的信息增益值,计算如下所示:
1 |
Gain(OUTLOOK) = Info(D) - Info(OUTLOOK) = 0.940 - 0.694 = 0.246 |
2 |
Gain(TEMPERATURE) = Info(D) - Info(TEMPERATURE) = 0.940 - 0.911 = 0.029 |
3 |
Gain(HUMIDITY) = Info(D) - Info(HUMIDITY) = 0.940 - 0.789 = 0.151 |
4 |
Gain(WINDY) = Info(D) - Info(WINDY) = 0.940 - 0.892 = 0.048 |
接下来,我们计算分裂信息度量H(V):
- OUTLOOK属性
属性OUTLOOK有3个取值,其中Sunny有5个样本、Rainy有5个样本、Overcast有4个样本,则
1 |
H(OUTLOOK) = - 5/14 * log2(5/14) - 5/14 * log2(5/14) - 4/14 * log2(4/14) = 1.577406282852345 |
- TEMPERATURE属性
属性TEMPERATURE有3个取值,其中Hot有4个样本、Mild有6个样本、Cool有4个样本,则
1 |
H(TEMPERATURE) = - 4/14 * log2(4/14) - 6/14 * log2(6/14) - 4/14 * log2(4/14) = 1.5566567074628228 |
- HUMIDITY属性
属性HUMIDITY有2个取值,其中Normal有7个样本、High有7个样本,则
1 |
H(HUMIDITY) = - 7/14 * log2(7/14) - 7/14 * log2(7/14) = 1.0 |
- WINDY属性
属性WINDY有2个取值,其中True有6个样本、False有8个样本,则
1 |
H(WINDY) = - 6/14 * log2(6/14) - 8/14 * log2(8/14) = 0.9852281360342516 |
根据上面计算结果,我们可以计算信息增益率,如下所示:
1 |
IGR(OUTLOOK) = Info(OUTLOOK) / H(OUTLOOK) = 0.246/1.577406282852345 = 0.15595221261270145 |
2 |
IGR(TEMPERATURE) = Info(TEMPERATURE) / H(TEMPERATURE) = 0.029 / 1.5566567074628228 = 0.018629669509642094 |
3 |
IGR(HUMIDITY) = Info(HUMIDITY) / H(HUMIDITY) = 0.151/1.0 = 0.151 |
4 |
IGR(WINDY) = Info(WINDY) / H(WINDY) = 0.048/0.9852281360342516 = 0.048719680492692784 |
根据计算得到的信息增益率进行选择属性集中的属性作为决策树结点,对该结点进行分裂。
C4.5算法的优点是:产生的分类规则易于理解,准确率较高。
C4.5算法的缺点是:在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效。