动态规划 ( DP ) 和 实例分析
一直都不知道怎么来写这篇博文,真的很难写,主要是怕自己写不好,会造成误解!因为之前自己看的网上的一些文章就是的,不过也有好的~感谢那些大牛!
现在也尝试写吧,写的不好,大家请包涵见谅!
我一般是比较讨厌在bolg上写概念的,因为那真的很无聊,但并不是概念不重要,很重要,但是写出来应该要用比较好理解的描述。一直尝试着怎么去很好的描述DP,也一直在纠结!很多时候是会这一个DP的题目,下一个还是不会,这样真的没什么用,其实对于我自己来说,也是的!悲哀~
好了,不多废话!
我这里说的都是建立在可以DP的情况下!
DP:简单来说就是
1:将一个大的问题小化
2:需要保存小问题的值,来给大的问题使用,或者说直接调用(其实也就是空间换时间)
关键:怎样找到那个小问题,或者说怎么去划分小状态!
同时我觉得,有时候并不一定要写出动态规划的方程,很多时候只是考虑清楚有哪些情况就可以了~
其实到这个地方我就不知道怎么去解释了,因为对于每一个问题来说是不一样的!
或许可以这么想,如果你会这个问题的递归算法,递归是将问题不断减小,然后作为返回参数!那么对于DP来说,不是从大问题开始减小,而是从小问题开始增大,然后解决后面大问题的时候,直接调用前面小问题的解就可以!所以过程基本与递归式相反的!
看个小例子:fibonacci 序列
如果我们使用递归,那么是
int fun( int n )
{
if( n == 0 || n == 1 )
{
return 1;
}
else
{
return fun( n - 1 ) + fun( n - 2 );
}
}
那么对于fun( n - 1 ) 和 fun( n - 2 )来说,对于子问题都要重复计算( 显然是吧,因为2个都要递归到最小值0和1 ),那么就是很浪费时间不是吗?
对于DP来说,采用保存小问题的办法,看代码
int a[n];
a[0] = 1;
a[1] = 1;
for( i = 2; i < n; ++i )
{
a[i] = a[i-1] + a[i-2]; // 每一个子问题都被记录,那么只需计算一次子问题就ok
}
ok,基本的情况我们已经知道,那么下面看看一些经典的DP问题吧~
一:装配线调度
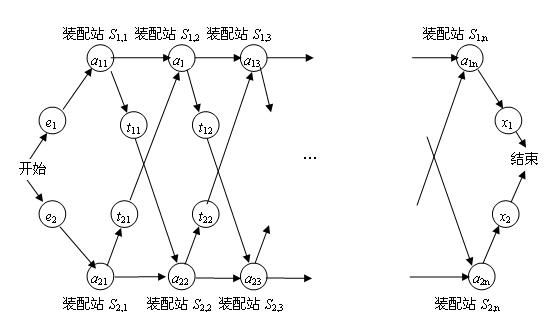
Colonel汽车公司在有两条装配线的工厂内生产汽车,一个汽车底盘在进入每一条装配线后,在每个装配站会在汽车底盘上安装不同的部件,最后完成的汽车从装配线的末端离开。如下图所示。
每一条装配线上有n个装配站,编号为j=1,2,...,n,将装配线i(i为1或2)的第j个装配站表示为S(i,j)。装配线1的第j个站S(1,j)和装配线2的第j个站S(2,j)执行相同的功能。然而这些装配站是在不同的时间建造的,并且采用了不同的技术,因此,每个站上完成装配所需要的时间也不相同,即使是在两条装配线上相同位置的装配站也是这样。把每个装配站上所需要的装配时间记为a(i,j),并且,底盘进入装配线i需要的时间为e(i),离开装配线i需要的时间是x(i)。正常情况下,底盘从一条装配线的上一个站移到下一个站所花费的时间可以忽略,但是偶尔也会将未完成的底盘从一条装配线的一个站移到另一条装配线的下一站,比如遇到紧急订单的时候。假设将已经通过装配站S(i,j)的底盘从装配线i移走到另一条装配线所花费的时间为t(i,j),现在的问题是要确定在装配线1内选择哪些站以及在装配线2内选择哪些站,以使汽车通过工厂的总时间最小。
这里我们就直接用DP的思想去考虑问题:我们需要求最短路径,那么对于中间的任意一点来说,只可能有两路径到达自己,从自己这条线的前一个节点,或者是从对面那一条线的对应的前一个节点,那么这题是典型的DP问题,我们从前到后,把每一级的最优解求出来,然后供后面的大问题处理即可!!所以我们需要一个数组来记录每一级的最短的路径值,暂且设为A[2][N],因为只有两条线,那么A[0][i]代表第一条线的第i个节点的情况;
A[1][i]代表的是第二条线的第i个节点的情况;
其实这一题我们不需要写出状态方程式可以的,我们很清楚最有解只有2个方向过来的,如果从自己的前一个节点来( 例如现在考虑的是第一条线上的点 ),那么就是 A[0][i-1] + cost[i],如果从对面线的对应前一个节点来,那么就是 A[1][i-1] + cost[i] + t ( t是从对面过来的代价 )
那么去 A[0][i] = min(A[0][i-1] + cost[i],A[1][i-1] + cost[i] + t ) 也就是所谓的状态方程,所以后面的大问题都是由小问题保存的解推出来的!所以DP很方便!
演示参考代码如下:
#include <stdio.h>
#define N 6
typedef struct
{
int id;
int parent_line;// 为了最后得到路线的序列设置
int parent_id; // 同上
int w; // 本节点的权值
int to_next_w; // 跳转到对面对应下一个经过的时间装配线
}DATA, *pData;
int min( int a, int b, int *parent )
{
if( a < b )
{
*parent = 1;
return a;
}
else
{
*parent = 2;
return b;
}
}
int main()
{
DATA nodes[2][N]; // 每个点的信息
int all_ans[2][N]; // 记录
int init_1_w, init_2_w;// 刚刚开始进入时时间代价
// 进入两条路线的消耗不一定一样
int i;
int parent, parent_id, parent_line, tmp_id, tmp_line;
printf("\n输入第一条流线信息:");
for( i = 0; i < N; i++ )
{
printf("\n输入%d点权值和转移时间:", i + 1);
scanf("%d%d", &nodes[0][i].w, &nodes[0][i].to_next_w);
nodes[0][i].id = i + 1;
}
printf("\n输入第二条流线信息:");
for( i = 0; i < N; i++ )
{
printf("\n输入%d点权值和转移时间:", i + 1); // 所谓转移时间就是从此点到对面对应下一个点的代价
scanf("%d%d", &nodes[1][i].w, &nodes[1][i].to_next_w);
nodes[1][i].id = i + 1 + N;
}
printf("\n输入初始化进入两条流线的时间消耗:");
scanf("%d%d", &init_1_w, &init_2_w );
// 下面就是正式的DP的过程
//
all_ans[0][0] = init_1_w + nodes[0][0].w; // 初始化
all_ans[1][0] = init_2_w + nodes[1][0].w;
for( i = 1; i < N; i++ )
{
// 下面处理流线1
parent = -1;
all_ans[0][i] = min( all_ans[0][i-1] + nodes[0][i].w, all_ans[1][i-1] + nodes[0][i].w + nodes[1][i-1].to_next_w, &parent );
if( parent == 1 ) // 说明是从第一条线来的最优解
{
nodes[0][i].parent_line = 0; // 那么记录此点的来的方向是0,代表第一条线
nodes[0][i].parent_id = nodes[0][i-1].id - 1;
}
else if( parent == 2 )
{
nodes[0][i].parent_line = 1;
nodes[0][i].parent_id = nodes[1][i-1].id - N - 1; // - N 是为了转化为正常的数组idx
}
// 下面处理流线2
parent = -1;
all_ans[1][i] = min( all_ans[0][i-1] + nodes[1][i].w + nodes[0][i-1].to_next_w, all_ans[1][i-1] + nodes[1][i].w, &parent );
if( parent == 1 )
{
nodes[1][i].parent_line = 0;
nodes[1][i].parent_id = nodes[0][i-1].id - 1;
}
else if( parent == 2 )
{
nodes[1][i].parent_line = 1;
nodes[1][i].parent_id = nodes[1][i-1].id - N - 1;
}
}
all_ans[0][N-1] += nodes[0][N-1].to_next_w; // 注意最后出流水线的时候还有时间!
all_ans[1][N-1] += nodes[1][N-1].to_next_w;
if( all_ans[0][N-1] > all_ans[1][N-1] ) // 求出最小消耗
{
printf("最小时间消耗:%d\n", all_ans[1][N-1]);
printf("%d <- ", nodes[1][N-1].id);
parent_id = nodes[1][N-1].parent_id;
parent_line = nodes[1][N-1].parent_line;
}
else
{
printf("最小时间消耗:%d\n", all_ans[0][N-1]);
printf("%d <- ", nodes[0][N-1].id);
parent_id = nodes[0][N-1].parent_id;
parent_line = nodes[0][N-1].parent_line;
}
// 下面遍历其他nodes
//
for( i = N - 1; i > 0; --i )
{
printf("%d <- ", nodes[parent_line][parent_id].id);
tmp_id = nodes[parent_line][parent_id].parent_id;
tmp_line = nodes[parent_line][parent_id].parent_line;
parent_line = tmp_line;
parent_id = tmp_id;
}
return 0;
}

二:最长递增序列和最长不递增序列( LIS问题 )
写一个时间复杂度尽可能低的程序,求一个一维数组(N个元素)中的最长递增子序列的长度。
分析:例如
举例:
原序列为A[] = { 10,50,80,30,60,70 }
B[] = { ... }
开始遍历A,如果遇到B[top] < A[i],那么说明是符合递增序列的性质的,那么B[++top] = A[i],再接着扫描
如果发现B[top] <= A[i],那么我们知道这个数据会影响序列递增,那么我们需要怎么办?我们尽可能要保证每一个子序列都是尽可能的递增,那么我们需要在B[0]---B[top]找到第一大于A[i]的数(使用二分法,那么节约了时间!),下标为x,然后B[x] = A[i];为什么找第一个大于A[i]的数呢?就是为了使得各个子序列尽可能的增序( 此处我也不知道怎么去描述,大家自己也好好想想,很多时候讲不出来,无语~~~)。
那么我们看过程:
B[0] = 10; //
B[1] = 50;
B[2] = 80;
// 前面三个都是属于B[top] < A[i],所以加进去即可
再读到30,用30替换50,得到10,30,80; ( 使用二分法 )
再读60,用60替换80,得到10,30,60;再读70,得到最终栈为10,30,60,70。最长递增子序列为长度4。
代码如下:
#include <stdio.h>
#include <stdlib.h>
int main()
{
int n, i;
int *save, *mat, top, low, high, mid;
scanf("%d", &n);
save = ( int* )malloc( sizeof( int ) * n );
mat = ( int* )malloc( sizeof( int ) * n );
for( i = 0; i < n; ++i )
{
scanf("%d", &mat[i]);
}
save[0] = mat[0];
top = 0;
for( i = 1; i < n; ++i )
{
if( save[top] < mat[i] )
{
save[++top] = mat[i];
}
else
{
// 使用二分法得到第一个大于mat[i]的位置
//
low = 0;
high = top;
while( low <= high )
{
mid = ( low + high ) / 2;
if( mat[i] > save[mid] )
{
low = mid + 1;
}
else
{
high = mid - 1;
}
}
save[low] = mat[i];
}
}
printf("最长长度为:%d\n", top + 1);
for( i = 0; i <= top; ++i ) // 注意此处只能得到一个序列,可能有多个呢~
{
printf("%d ", save[i]);
}
printf("\n");
free( save );
free( mat );
return 0;
}
对于最长不递增序列也是一样的~
三:LCS问题
同样为了记录子问题,也需要数组S[i][j]记录,表示A序列前i个元素和B序列前j个元素最大的公共序列!
对于两个序列,求最大公共序列,对于此题一般会分成三种判断规则:
如果A[i] == B[j] 那么S[i][j] = S[i-1][j-1] + 1;
如果A[i] != B[j] 那么
-> 取S[i][j] = max( S[i-1][j], S[i][j-1] ); // 去子序列中公共部分较长的一个~好理解
基本的DP思想就是这样的;
代码如下:
// 主要是使用一个记录数组c[i][j]表示str1前i个字符和str2前j个字符的匹配长度
#include <stdio.h>
#include <string.h>
// 递归输出
//
void print_lcs( int b[80][80], char str[80], int l1, int l2 )
{
if( l1 == 0 || l2 == 0 )
{
return;
}
if( b[l1][l2] == 0 ) // 此位置匹配!
{
print_lcs( b, str, l1 - 1, l2 - 1 );
printf("%c ", str[l1-1]);
}
else if( b[l1][l2] == 1 )
{
print_lcs( b, str, l1 - 1, l2 );
}
else
{
print_lcs( b, str, l1, l2 - 1 );
}
}
int main()
{
char str1[80], str2[80];
int i, j, len1, len2;
int c[80][80]; // 用于记录 : 注意下标代表的是前面处理的 !长度!
int b[80][80];
gets( str1 );
gets( str2 );
len1 = strlen( str1 );
len2 = strlen( str2 );
for( i = 0; i <= len1; ++i ) // 因为是 c[][0] ,第二个长度=0,所以不可能有匹配,所以是0
{
c[i][0] = 0;
}
for( j = 0; j <= len2; ++j ) // 同上
{
c[0][j] = 0;
}
for( i = 1; i <= len1; ++i )
{
for( j = 1; j <= len2; ++j )
{
if( str1[i-1] == str2[j-1] ) // 此位置上匹配
{
c[i][j] = c[i-1][j-1] + 1; // 公共长度+1很好理解
b[i][j] = 0; // 已经匹配
}
else if( c[i-1][j] >= c[i][j-1] )
{
c[i][j] = c[i-1][j];
b[i][j] = 1;
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = 2;
}
}
}
printf("最长公共序列长度:%d\n", c[len1][len2]);
print_lcs( b, str1, len1, len2 );
puts("");
return 0;
}
四:最后一个实例想说说0-1背包问题
假设w1, ..., wn和W都是正整数。我们将在总重量不超过Y的前提下,前j种物品的总价格所能达到的最高值定义为A(j, Y)。
A(j, Y)的递推关系为:
A(0, Y) = 0
A(j, 0) = 0
如果wj > Y, A(j, Y) = A(j - 1, Y)
如果wj <= Y, A(j, Y) = max { A(j - 1, Y), pj + A(j - 1, Y - wj) }
最后一个公式的解释:总重量为Y时背包的最高价值可能有两种情况,第一种是在Y重量下,可以在前j - 1个物品中得到最大价值,
这对应于表达式A(j - 1,Y)。第二种是包含了第j个物品,那么对于前j-1个物品,可以在重量为Y-wj的情况下找到最大价值,
综合起来就是pj + A(j - 1, Y - wj)。
说白了就是:从第一个物品开始,对于每考虑增加一个物品,就考虑w从1->max情况
例如:
!!!感谢实例来源:http://blog.csdn.net/hanruikai/article/details/7471258
| 0 | 李子 | 4KG | NT$4500 |
| 1 | 苹果 | 5KG | NT$5700 |
| 2 | 橘子 | 2KG | NT$2250 |
| 3 | 草莓 | 1KG | NT$1100 |
| 4 | 甜瓜 | 6KG | NT$6700 |
- 放入李子
| 背包负重 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| value | 0 | 0 | 0 | 4500 | 4500 | 4500 | 4500 | 9000 |
| item | - | - | - | 0 | 0 | 0 | 0 | 0 |
- 放入苹果
| 背包负重 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| value | 0 | 0 | 0 | 4500 | 5700 | 5700 | 5700 | 9000 |
| item | - | - | - | 0 | 1 | 1 | 1 | 0 |
- 放入橘子
| 背包负重 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| value | 0 | 2250 | 2250 | 4500 | 5700 | 6750 | 7950 | 9000 |
| item | - | 2 | 2 | 0 | 1 | 2 | 2 | 0 |
- 放入草莓
| 背包负重 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| value | 1100 | 2250 | 3350 | 4500 | 5700 | 6800 | 7950 | 9050 |
| item | 3 | 2 | 3 | 0 | 1 | 3 | 2 | 3 |
- 放入甜瓜
| 背包负重 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| value | 1100 | 2250 | 3350 | 4500 | 5700 | 6800 | 7950 | 9050 |
| item | 3 | 2 | 3 | 0 | 1 | 3 | 2 | 3 |
我们可以得到最大的值是在最后一个水果放进去,且达到最大的W的时候的值,也就是 在背包负重8公斤时,最多可以装入9050元的水果,然后将对应的水果的weight、减去得到8-1=7,那么找w=7时候的最佳解即7950,然后再减去对应水果weight即7-2=5,w=5时候最佳值就是5700,然后5-5=0,ok结束!
代码如下:
#include <stdio.h>
#include <stdlib.h>
#define MAX_OBJ 10
#define MAX_WEI 100
typedef struct
{
int weight;
int value;
}good, *p_good;
int dp_get_max_value( good goods[], int n, int w )
{
int result[MAX_OBJ+1][MAX_WEI+1]; // 存放最终的放入的物品情况!
int tmp[MAX_OBJ+1][MAX_WEI+1]; // 代表选择几件物品i,在可承受重量j情况下的最大的价值
int i, j, x, y;
for( i = 0; i < n + 1; ++i )
{
tmp[i][0] = 0; // 可承受价值为0,那么任意件物品都放不进,所以 = 0;
}
for( i = 0; i < w + 1; ++i )
{
tmp[0][i] = 0; // 即使有可以承受的重量,但是我一件物品都不放,那么价值还是 = 0;
}
i = 1;
while( i <= w ) // 初始化第一个物品的数据
{
if( goods[0].weight > i )
{
result[1][i] = -1;
}
else
{
result[1][i] = 0;
}
tmp[1][i] = ( int )( i / goods[0].weight ) * goods[0].value;
++i;
}
for( i = 1; i < n; ++i )
{
for( j = 1; j < w + 1; ++j )
{
if( goods[i].weight > j )
{
tmp[i+1][j] = tmp[i][j];
result[i+1][j] = result[i][j];
}
else
{
tmp[i+1][j] = tmp[i][j] > ( tmp[i][j-goods[i].weight] + goods[i].value ) ? tmp[i][j] : ( tmp[i][j-goods[i].weight] + goods[i].value );
if( tmp[i+1][j] == tmp[i][j] ) //
{
result[i+1][j] = result[i][j];
}
else
{
result[i+1][j] = i;
}
}
}
}
/*
for( i = 1; i <= n; ++i )
{
for( j = 1; j <= w; ++j )
{
printf("%d ", result[i][j]);
}
printf("\n");
}
*/
printf("选出的物品的id为: ");
x = n;
y = w;
while( y ) // 找到所有的id
{
printf("%d ", result[n][y]);
y -= goods[result[n][y]].weight;
}
printf("\n");
return tmp[n][w];
}
int main()
{
int n, i, w;
p_good goods;
printf("输入能承受的最大重量:");
scanf("%d", &w);
printf("\n输入物品的种类个数:");
scanf( "%d", &n );
goods = ( p_good )malloc( sizeof( good ) * n );
printf("\n输入物品的重量和价值:\n");
for( i = 0; i < n; ++i )
{
scanf("%d%d", &goods[i].weight, &goods[i].value);
}
printf("最大价值是:%d\n", dp_get_max_value( goods, n, w ));
return 0;
}
说到现在,感觉有点崩溃,感觉讲解的真烂,哎,大家见谅!
希望能与大家共同学习!谢谢~