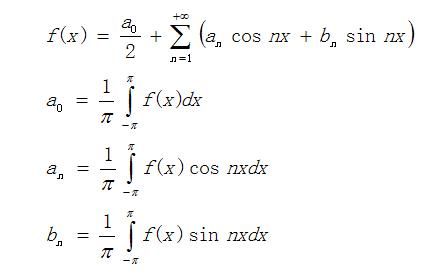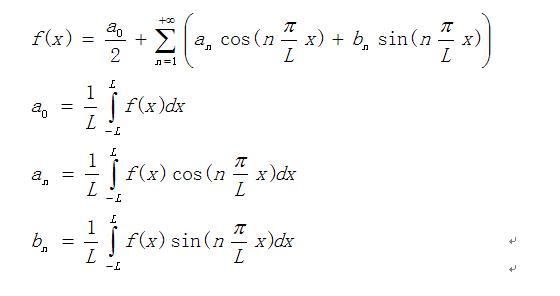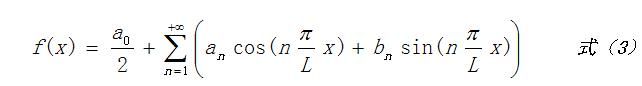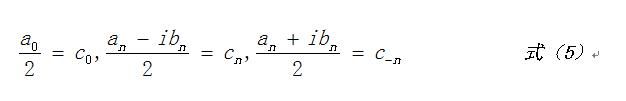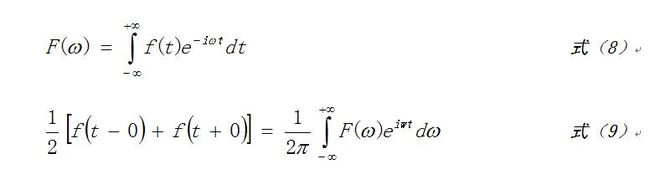重温傅里叶—笔记篇
本文记录的大多是基础的公式,还有一些我认为比较重要的有参考价值的说明。(如果对这些公式已经很熟悉,可以直接看第三部分:总结性说明)
重温傅里叶—笔记篇
一、傅里叶级数
$ 关于三角函数系的正交性:
三角函数系包括:
1, cos x, sinx , cos2x, sin 2x, …… cos nx, sinnx, ……
“正交性”是说,三角函数系中的任何一项与另一项的乘积,在 (-π, π) 区间内的积分为0。(任何两相的积总可以展成两个频率为整数倍基频的正余弦函数之和或差,而这两个展开后的正余弦在(-π, π)上积分都为0)。
不同频率(但都是整数倍基频)的两个正弦函数之积,在(-π, π)上积分恒为0。
同频率的两个正弦函数之积,只有在这两个正弦的相位正交时,其在(-π, π)上积分才是0。
三角函数系中除“1”以外的任何一项的平方,在(-π, π)上的积分恒为π,“1”在这个区间上的积分为2π。
$
上公式 !
① 当周期为2π时:
式(1):
上式成立的条件是f(x)满足狄立克雷充分条件:
1. 在任意有限区间内连续,或只有有限多个第一类间断点;
2. 任意的有限区间,都可被分成有限多个单调区间(另一种说法是:任意有限区间内只有有限多个极值点,其实是一样的)
式(1)第一行中的a0/2 就是f(x)的周期平均值,而且第一行的式子只对f(x)是连续函数的情况成立;如果f(x)不连续,则应表示成“(1/2) ×[f(x-0)+f(x+0)]”,即f(x)左右极限的算术平均。下面的类似情况都是这样,之后就不再专门说明,这些大家应该都懂。
第三、四行中,n的取值都是:1,2,3,4,……n,……(都为正,且不包含0)。
② 当周期为2L时(这也是最一般的情形):
式(2):
第一行中的a0/2 就是f(x)的周期平均值;
第三、四行中,n的取值都是:1,2,3,4,……n,……(都为正,且不包含0)。
$ 傅里叶级数的复数表达方式
同样设周期为2L。根据欧拉公式,正余弦函数都可以用复指数表示出来。这样上面式(2)中的第一行:
可以表示为:
令:
cn与c-n互为共轭。这样式(4)变为:
由式(5)和式(2)中对 a0 b0an bn c0 cn c-n的定义,可以发现cn可统一表达为:
将傅里叶级数用复数表示后,就是式(6)和式(7)这样简洁的形式。
简单分析:
② 若f(x)为偶(或奇)函数,则所有的bn(或an)将为0,此时的cn将变为实数(或纯虚数),且an(或bn)是转换后所得的cn的2(或2i)倍,而c-n与cn相等(或纯虚共轭)。
二、复变函数中的傅里叶变换
$ 先上公式:
定理:若f(t)在(-∞,+∞)上绝对可积,即 f(t)的绝对值在(-∞,+∞)上收敛,则F(ω)在(-∞,+∞)上存在且连续(F(ω)的连续性在复变函数的教科书中一般都有证明)。F(ω)是实变复值函数,即变量ω是在实数区间(-∞,+∞)定义,而函数值F(ω)却在复数空间。
式(9)的条件是:f(t)在(-∞,+∞)上绝对可积,并在任一有限区间 满足狄立克雷充分条件。
$ 若f(t)为偶函数,则F(ω)将为纯实数,且同为偶函数;
若f(t)为奇函数,则F(ω)将为纯虚数,且同为奇函数;
而对任意f(t),F(ω) 与F(-ω)始终共轭,这意味着 |F(ω)| 与 | F(-ω)| 恒相等,即F(ω)的绝对值是偶函数。
$ 由于要求f(t)绝对可积,所以对于周期函数一般是不能用傅里叶变换的,只能用傅里叶级数分析。(周期函数往往不能收敛)。
三、总结性说明
周期函数可以看成由很多频率是原函数频率整数倍的正余弦波叠加而成,每个频率的波都有各自的振幅和相位,必须将所有频率的振幅和相位同时记录才能准确表达原函数。但从上面的公式来看,我们好像从没涉及到相位?其实不然,从式(2)来看,我们将每个频率的波分成了一个正弦分量和一个余弦分量,同时记录了这两个分量的振幅an、bn其实就已经包含了这个频率的波的相位信息;而对于式(6a),每个频率的波被分成了正负两个频率的复数“波”,这种方式其实比正余弦形式更加直观,因为复振幅cn恰好同时记录了这个频率的振幅和相位,它的物理意义很明显:cn的幅值 |cn| 即为该频率的振幅(准确的说是振幅的一半),而其辐角恰好就是相位(准确的说是反相的相位,c-n的辐角才恰好代表该频率波分量的相位)。
傅里叶变换针对的是非周期函数,或者说,周期为无穷的函数。它是傅里叶级数的一个特例(好吧,我曾经一直以为傅里叶级数是傅里叶变换的一个特例,正好相反,刚前几天才想通透)。当傅里叶级数的周期L趋于无穷时,自然就变成了上面的傅里叶变换。这种关系从二者的表达式中大概能看出点端倪,但是也不是特别明显,毕竟它们的表达形式差别还挺大。如果不把傅里叶级数表达成复数形式,那就更加难看出二者之间的联系了,这也是为什么本文中详细列出了复数形式的傅里叶级数。傅里叶变换要求f(t)在(-∞,+∞)上绝对可积,其实可以理解成“傅里叶级数要求函数在一个周期内的积分必须收敛”。在深入篇中,我再好好说说二者是如何联系的。