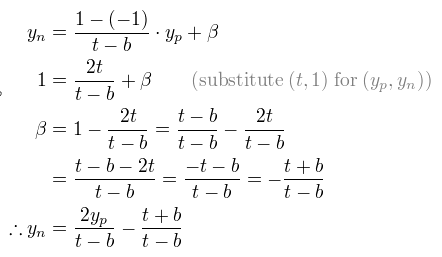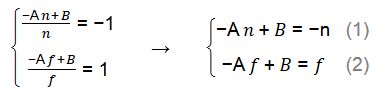Qt OpenGL:学习现代3D图形编程之四,透视投影
一、非真实的世界
与之前几篇文章不同的是,这里要画12个三角形,这个12个三角形构造一个方形棱柱(这里为长方体)。棱柱的每个四边形表面由两个三角形组成。这两个三角形其中的一条边重合,而且它们的六个顶点的颜色相同,因此每个四边形表面都有唯一的颜色。下面的顶点着色器我们已经非常熟悉,它传递颜色到片段着色器,定义了一个uniform的二维向量offset,该变量用来改变顶点位置的x和y坐标值。
const std::string strVertexShader(
"#version 330\n"
"layout(location = 0) in vec4 position;\n"
"layout(location = 1) in vec4 color;\n"
"smooth out vec4 theColor;\n"
"uniform vec2 offset;\n"
"void main()\n"
"{\n"
" gl_Position = position + vec4(offset.x, offset.y, 0.0, 0.0);\n"
" theColor = color;\n"
"}\n"
);
片段着色器只是简单的用顶点着色器传过来的颜色进行插值运算并输出。const std::string strFragmentShader(
"#version 330\n"
"out vec4 outputColor;\n"
"smooth in vec4 theColor;\n"
"void main()\n"
"{\n"
" outputColor = theColor;\n"
"}\n"
);
绘制方形棱柱使用的顶点数组如下所示。const float vertexData[] = {
0.25f, 0.25f, 0.75f, 1.0f,
0.25f, -0.25f, 0.75f, 1.0f,
-0.25f, 0.25f, 0.75f, 1.0f,
0.25f, -0.25f, 0.75f, 1.0f,
-0.25f, -0.25f, 0.75f, 1.0f,
-0.25f, 0.25f, 0.75f, 1.0f,
0.25f, 0.25f, -0.75f, 1.0f,
-0.25f, 0.25f, -0.75f, 1.0f,
0.25f, -0.25f, -0.75f, 1.0f,
0.25f, -0.25f, -0.75f, 1.0f,
-0.25f, 0.25f, -0.75f, 1.0f,
-0.25f, -0.25f, -0.75f, 1.0f,
-0.25f, 0.25f, 0.75f, 1.0f,
-0.25f, -0.25f, 0.75f, 1.0f,
-0.25f, -0.25f, -0.75f, 1.0f,
-0.25f, 0.25f, 0.75f, 1.0f,
-0.25f, -0.25f, -0.75f, 1.0f,
-0.25f, 0.25f, -0.75f, 1.0f,
0.25f, 0.25f, 0.75f, 1.0f,
0.25f, -0.25f, -0.75f, 1.0f,
0.25f, -0.25f, 0.75f, 1.0f,
0.25f, 0.25f, 0.75f, 1.0f,
0.25f, 0.25f, -0.75f, 1.0f,
0.25f, -0.25f, -0.75f, 1.0f,
0.25f, 0.25f, -0.75f, 1.0f,
0.25f, 0.25f, 0.75f, 1.0f,
-0.25f, 0.25f, 0.75f, 1.0f,
0.25f, 0.25f, -0.75f, 1.0f,
-0.25f, 0.25f, 0.75f, 1.0f,
-0.25f, 0.25f, -0.75f, 1.0f,
0.25f, -0.25f, -0.75f, 1.0f,
-0.25f, -0.25f, 0.75f, 1.0f,
0.25f, -0.25f, 0.75f, 1.0f,
0.25f, -0.25f, -0.75f, 1.0f,
-0.25f, -0.25f, -0.75f, 1.0f,
-0.25f, -0.25f, 0.75f, 1.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.8f, 0.8f, 0.8f, 1.0f,
0.8f, 0.8f, 0.8f, 1.0f,
0.8f, 0.8f, 0.8f, 1.0f,
0.8f, 0.8f, 0.8f, 1.0f,
0.8f, 0.8f, 0.8f, 1.0f,
0.8f, 0.8f, 0.8f, 1.0f,
0.0f, 1.0f, 0.0f, 1.0f,
0.0f, 1.0f, 0.0f, 1.0f,
0.0f, 1.0f, 0.0f, 1.0f,
0.0f, 1.0f, 0.0f, 1.0f,
0.0f, 1.0f, 0.0f, 1.0f,
0.0f, 1.0f, 0.0f, 1.0f,
0.5f, 0.5f, 0.0f, 1.0f,
0.5f, 0.5f, 0.0f, 1.0f,
0.5f, 0.5f, 0.0f, 1.0f,
0.5f, 0.5f, 0.0f, 1.0f,
0.5f, 0.5f, 0.0f, 1.0f,
0.5f, 0.5f, 0.0f, 1.0f,
1.0f, 0.0f, 0.0f, 1.0f,
1.0f, 0.0f, 0.0f, 1.0f,
1.0f, 0.0f, 0.0f, 1.0f,
1.0f, 0.0f, 0.0f, 1.0f,
1.0f, 0.0f, 0.0f, 1.0f,
1.0f, 0.0f, 0.0f, 1.0f,
0.0f, 1.0f, 1.0f, 1.0f,
0.0f, 1.0f, 1.0f, 1.0f,
0.0f, 1.0f, 1.0f, 1.0f,
0.0f, 1.0f, 1.0f, 1.0f,
0.0f, 1.0f, 1.0f, 1.0f,
0.0f, 1.0f, 1.0f, 1.0f,
};
在初始化时引入了三个新函数,它们分别是glEnable,glCullFace和glFrontFace。glEnable函数是一个多功能工具,OpenGL的很多状态可以通过这些状态的标识来设置,glEnable可以把标志设置为“on”(启用),与此同时,glDisable能把标志设置为“off”(停用)。当启用GL_CULL_FACE标志时,OpenGL会激活表面剔除(face culling),之前的渲染都没有使用表面剔除。表面剔除在提高性能方面是一个非常有用的特性。以方形棱柱为例,或者更具体一点,拿起一个遥控器,不管遥控器在眼前如何摆放,或者从任何方位去观察,我们都最多只能看到遥控器的三个表面。因此,为什么要耗费大量片段处理时间用于另外三个表面的渲染?GL_CULL_FACE的使命就是告诉OpenGL,不要去渲染一个物体中我们看不到的表面。在窗口空间,我们可以看到渲染后的三角形。其实每个三角形的顶点是按照特定的顺序提供给OpenGL的。不管三角形的形状如何,我们可以将三角形的顶点顺序分为两类-顺时针环绕和逆时针环绕。如果三个顶点时按照顺时钟环绕的顺序提供给OpenGL,那么在窗口空间中,我们看到的这个三角形相对于我们就算顺时针的,反之亦然。表面剔除就是基于环绕方向的,设置环绕方向分为两个步骤,分别由函数glCullFace和glFrontFace实现。glFrontFace指定了环绕方向,它指定的环绕方向将被认为是三角形的前面,它的参数值为GL_CW或者GL_CCW,分别对应顺时针方向和逆时针方向,默认值为GL_CCW。glCullFace指定被剔除的表面,是前面、后面或者两面都剔除,相应的参数值为GL_FRONT、GL_BACK或者GL_FRONT_AND_BACK。由顶点数组vertexData可以看最开始的两个三角形的顶点数据是按照顺时针环绕方向提供的。因此当glFrontFace参数为GL_CW时,在窗口空间中看到的由这两个三角形组成的四边形表面就是前面,这样当调用glCullFace(GL_BACK)时,该四边形表面不会被剔除。三角形顶点的环绕方向如下图所示。
新的初始化函数如下所示。
void init()
{
InitializeProgram();
InitializeVertexBuffer();
glEnable(GL_CULL_FACE);
glFrontFace(GL_CW);
glCullFace(GL_BACK);
}
初始化时,通过设置顶点着色器的offset变量,将方形棱柱渲染到窗口的右上角。
GLuint offsetUniform = glGetUniformLocation(theProgram, "offset"); glUseProgram(theProgram); glUniform2f(offsetUniform, 0.5f, 0.5f); glUseProgram(0);
由顶点数组vertexData可以看出,绘制出来的应该是一个方形棱柱,但是实际上绘制结果看上去就是一个在窗口右上角的正方形。再次拿起遥控,将某一面正对着视线的中心,我们也只能看到前面而看不到后面,此时把遥控器向视线的右上方移动,左面和下面就可以看到了。但是为什么看不到方形棱柱的左面和下面呢?这将是透视投影要解决的问题。
二、透视投影
我们在屏幕上看到的是一个二维的像素数组,我们使用的3D渲染管线定义了顶点位置从裁剪空间(clip space)到窗口空间的转换,一旦顶点位置转换到窗口空间,2D三角形就被渲染了。
投影,是渲染管线将世界进行维度转换的一种方式,我们的世界是三维的,渲染管线定义了从3D世界到2D世界的投影。2D世界中的三角形才是真正被渲染的。
1.正交投影
正交投影(orthographic projection)是一种非常简单的投影方式,当投影到轴对齐的表面时,只是把坐标垂直投射到该平面,如下图所示。
为了简单起见,2D场景被正交投影到黑色的直线上,灰色区域代表了投影时的可见区域,灰色区域外侧场景不会被看到。正交投影无法看到一个物体是远离我们还是正在我们面前。因为投影不会根据距离收缩,所以如果画一个固定大小的物体在视点前面,同时画一个同样大小的物体在这个物体的远后方,无法判断哪个物体是第一个。
2.透视投影
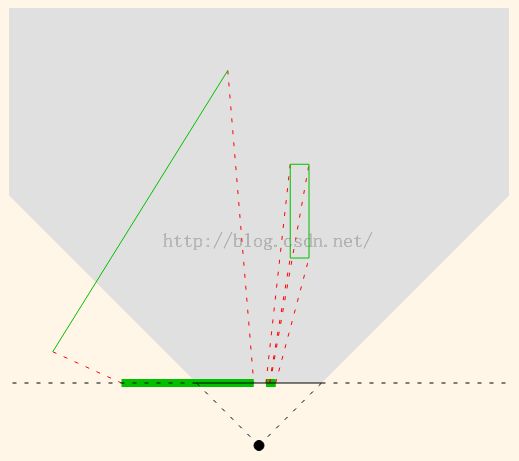
所以人的眼睛不是通过正交投影来看世界的,也就是说正交投影对于我们来说不太真实,要不然我们只能看到瞳孔大小的区域。实际上我们的视线与针孔相机的原理相同,该原理称为透视投影。例如,一个高个子的人站在你面前,他看上去是很高的。如果这个人站在100米以外,他看上去甚至还没有你的拇指大,但是我们实际上都知道,它依然是个高个子。2D到1D的透视投影如下图所示。
可以看出,透视投影是放射状的—基于特定的某个点,这个点就是我们眼睛或者相机的位置。从投影的形状可以看出,通过透视投影我们能够看到比正交投影大得多的区域。
3.透视投影矩阵的数学推导
OpenGL顶点的转换过程如下图所示。
OpenGL渲染的3D场景必须以2D形式的图像投影到屏幕上。GL_PROJECTION 矩阵就是用来设置投影变换的。首先,它将所有顶点从眼坐标(照相机坐标)转换到裁剪坐标系下。然后,这些裁剪坐标通过透视除法,即除以裁剪坐标中w分量,转换到归一化设备坐标系(NDC)。需要注意的是,裁剪(视锥剔除frustum culling)和NDC(normalized device coordinates)转换都集成到了GL_PROJECTION 矩阵。接下来的部分描述了怎么样通过left, right, bottom, top, near and far 这6个界限参数来构造投影矩阵。下图是进行过视锥剔除的三角形。
视锥剔除是在裁剪坐标系中进行的,并且恰好在透视除法之前进行。裁剪坐标xc, yc和zc 通过与wc比较来进行测试。如果某个坐标值比Wc小或者比Wc大,那么这个顶点将被丢弃。然后,OpenGL会重构剪裁后的多边形边缘。
实际上,眼坐标系下坐标在乘以投影矩阵后,裁剪测试和透视除法都是由GPU来执行的。而后面这两个过程处理的裁剪坐标系数据都是由投影矩阵变换的。
a.裁剪测试也即视锥剔除
-Wc < Xc,Yc,Zc < Wc
b.NDC透视除法
Xn = Xc / Wc Yn = Yc / Wc Zn = Zc / Wc
需要注意的是,我们在构造16个参数的投影矩阵的同时,不仅要考虑到裁剪,还要考虑到透视除法的过程。这样,最终的NDC坐标才会满足:-1 < Xn,Yn,Zn < 1
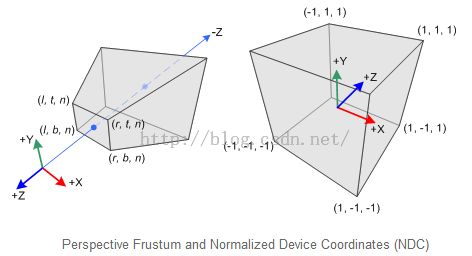
在进行透视投影时,眼坐标下截头椎体(a truncated pyramid frustum)内的3D点被映射到NDC下一个立方体中;x坐标从[l,r]映射到[-1,1],y坐标从[b,t]映射到[-1,1],z坐标从[n,f]映射到[-1,1]。
眼坐标系使用右手坐标系,而NDC使用左手坐标系。这就是说,眼坐标系下,在原点处的照相机朝着-Z轴看去,但是在NDC中它朝着+Z轴看去。因为glFrustum() 仅接受正的near和far距离,我们在构造GL_PROJECTION 矩阵时,需要取其相反数。眼坐标系和NDC坐标系如下图所示:
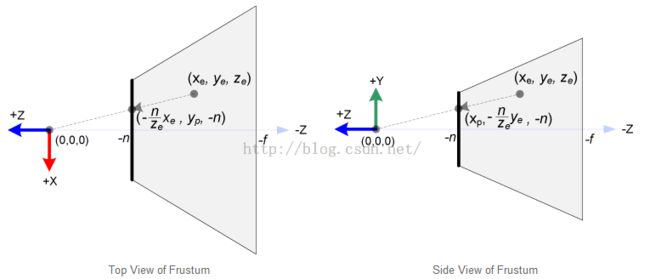
在OpenGL中,眼坐标下3D点被投影到近裁剪面(即投影平面)。下图展示了眼坐标系下点(xe, ye, ze) 如何投影到近裁剪面上的 (xp, yp, zp) 的。左侧是视锥的俯视图,右侧是视锥的侧视图。
根据三角形的相似性,由俯视图可得出:
由侧视图可以得出:
xp 和yp其实是一个中间值,我们要找的是(Xc, Yc, Zc)和 (Xn, Yn, Zn)之间的关系,但是可以利用上述公式计算的坐标做过渡:
需要注意的是,这里 xp 和yp 都依赖于ze,他们与-ze成反比。换句话说,他们都被-ze相除。这个是构造GL_PROJECTION矩阵最初的线索。在眼坐标通过乘以GL_PROJECTION来转换时,裁剪坐标系仍然是一个齐次坐标系。通过对裁剪坐标进行透视除法得到最终的NDC坐标。下图解释了这个过程:
因此我们可以把裁剪坐标系下的w分量设为-ze,那么GL_PROJECTION矩阵第4行变为(0, 0, -1, 0),如下所示:
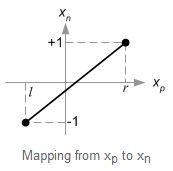
现在我们把xp和yp,映射到NDC中xn和yn,他们之间是线性关系: [l, r]⇒[-1, 1]和[b, t]⇒[-1, 1]。
线性关系如下图所示:
则可以推导出:
这个推导过程使用的就是简单的y=kx+b线性关系推导,同理利用[b, t]⇒[-1, 1]可推得:
将上面的 xp 和yp代入求得:
注意这里Xn和Yn已经是NDC中的坐标了,通过这两个坐标可以求出GL_PROJECTION的前两行来,如下所示:
现在只剩下矩阵的第三行了,因为Z值不依赖于x或者y,因此我们借用w分量来找出zn和ze之间的关系。因此我们可以这样指定第3行:
在眼坐标下We等于1,因此上式变为:
我们使用(ze, zn)的关系(-n, -1)和 (-f, 1)来求解出系数A,B;
使用消元法即可求出:
我们求出了A和B,那么ze和zn关系如下式:
最终的投影矩阵如下式:
这个公式对应的是一般的视锥,如果视锥是对称的,即r =-l ,t=-b,那么有:
4.方形棱柱的透视
为了简单起见,这里假设r=t,于是顶点着色器如下所示:
const std::string strVertexShader(
"#version 330\n"
"layout(location = 0) in vec4 position;\n"
"layout(location = 1) in vec4 color;\n"
"smooth out vec4 theColor;\n"
"uniform vec2 offset;\n"
"uniform float zNear;\n"
"uniform float zFar;\n"
"uniform float frustumScale;\n"
"void main()\n"
"{\n"
" vec4 cameraPos = position + vec4(offset.x, offset.y, 0.0, 0.0);\n"
" vec4 clipPos;\n"
" clipPos.xy = cameraPos.xy * frustumScale;\n"
" clipPos.z = cameraPos.z * (zNear + zFar) / (zNear - zFar);\n"
" clipPos.z += 2 * zNear * zFar / (zNear - zFar);\n"
" clipPos.w = -cameraPos.z;\n"
" gl_Position = clipPos;\n"
" theColor = color;\n"
"}\n"
);
这里的frustumScale=n/r=n/t,cameraPos即是眼坐标。在初始化时,设置顶点着色器的uniform变量值,如下所示。
GLuint frustumScaleUnif = glGetUniformLocation(theProgram, "frustumScale");
GLuint zNearUnif = glGetUniformLocation(theProgram, "zNear");
GLuint zFarUnif = glGetUniformLocation(theProgram, "zFar");
GLuint offsetUniform = glGetUniformLocation(theProgram, "offset");
glUseProgram(theProgram);
glUniform1f(frustumScaleUnif, 1.0f);
glUniform1f(zNearUnif, 1.0f);
glUniform1f(zFarUnif, 3.0f);
glUniform2f(offsetUniform, 0.5f, 0.5f);
渲染后的效果如下图所示。5.使用矩阵
一般来说,矩阵是一个二维的数据块。矩阵在计算机图形学中很常见。上一节中我们虽然实现了方形棱柱的透视,但是没有使用矩阵。随着我们对物体变换的细节越来越深入,我们将会越来越多的使用矩阵来简化计算。通常使用的是4*4的矩阵,即矩阵包含4行和4列,这是由物体本身的特性决定的,因为我们需要用矩阵来表示的物体不是三维的,就是三维加上一个额外的坐标数据。
现在我们将上一节的内容用矩阵来重新实现。使用矩阵时,顶点着色器变得更加简洁,如下所示。
const std::string strVertexShader(
"#version 330\n"
"layout(location = 0) in vec4 position;\n"
"layout(location = 1) in vec4 color;\n"
"smooth out vec4 theColor;\n"
"uniform vec2 offset;\n"
"uniform mat4 perspectiveMatrix;\n"
"void main()\n"
"{\n"
" vec4 cameraPos = position + vec4(offset.x, offset.y, 0.0, 0.0);\n"
" gl_Position = perspectiveMatrix * cameraPos;\n"
" theColor = color;\n"
"}\n"
);
矩阵是着色器语言包含的基本数据类型,矩阵和行数和列数可以是2到4的任意组合。正方形矩阵(行数和列数相同)矩阵可以用mat加上一个数字来指定,就像上面着色器中的mat4,mat4表示4*4的矩阵。对于非正方形矩阵,使用类似mat2x4的标记,表示矩阵包含2行和4列。
main函数的第二行用“*”运算符来表示矩阵乘法,要注意乘数和被乘数的顺序,因为矩阵乘法不满足交换律。下列算式就是由眼空间(照相机空间)转换到裁剪空间的矩阵表达式。
这样的话,如果用一维数组float theMatrix[16]来表示矩阵,那么theMatrix[0]=S;theMatrix[5]=S;theMatrix[10]=(F+N)/(N-F);theMatrix[11]=2FN/(N-F);theMatrix[14]=-1.0;其它的数组成员值为0。
根据上述分析,初始化时需添加下列代码。
GLuint perspectiveMatrixUnif = glGetUniformLocation(theProgram, "perspectiveMatrix");
GLuint offsetUniform = glGetUniformLocation(theProgram, "offset");
float fFrustumScale = 1.0f; float fzNear = 0.5f; float fzFar = 3.0f;
float theMatrix[16];
memset(theMatrix, 0, sizeof(float) * 16);
theMatrix[0] = fFrustumScale;
theMatrix[5] = fFrustumScale;
theMatrix[10] = (fzFar + fzNear) / (fzNear - fzFar);
theMatrix[11] = (2 * fzFar * fzNear) / (fzNear - fzFar);
theMatrix[14] = -1.0f;
glUseProgram(theProgram);
glUniformMatrix4fv(perspectiveMatrixUnif, 1, GL_TRUE, theMatrix);
glUniform2f(offsetUniform, 0.5f, 0.5f);
glUseProgram(0);
用一维数组来存储矩阵时,有两种方式。一是列优先存储,二是行优先存储。列优先存储时,从左到右,先存完第一列,再存第二列......,每列按照从上到下的顺序存储。行优先存储时,从上到下,先存第一行,再存第二行......,每行按照从左到右的顺序存储。上述代码中按照行优先存储。
为了把矩阵传递给OpenGL,我们使用了glUiformMatrix4fv函数,第一个参数是着色器中uniform变量的索引位置,第二个参数是矩阵数组个数,第三个参数是数组存储方式,GL_TRUE表示行优先存储,GL_FALSE表示列优先存储,最后一个参数表示数组本身。
渲染后的效果和上一节相同。
参考链接:http://alfonse.bitbucket.org/oldtut/Positioning/Tutorial%2004.html
参考链接:http://www.songho.ca/opengl/gl_projectionmatrix.html
参考链接:http://www.songho.ca/opengl/gl_transform.html
源码链接:见http://blog.csdn.net/caoshangpa/article/details/51049436的评论