拓扑排序算法
一,c语言的toposort
#include <iostream>
#include <stack>
using namespace std;
#define MAX_VERTEX_NUM 20
struct adjVertexNode //邻接表中的顶点
{
int adjVertexPosition; //当前点在图中的相邻的位置
adjVertexNode* next; //邻接表的下一个位置
};
struct VertexNode
{
char data[2]; //顶点的mark表示
adjVertexNode* list; //顶点构成的邻接表
int indegree; //顶点的入度信息
};
struct Graph
{
VertexNode VertexNode[MAX_VERTEX_NUM]; //顶点是用一个数组来存储的
int vertexNum; //图中顶点的数量
int edgeNum; //图中边的数量
};
void CreateGraph (Graph& g)
{
int i, j, edgeStart, edgeEnd;
adjVertexNode* adjNode;
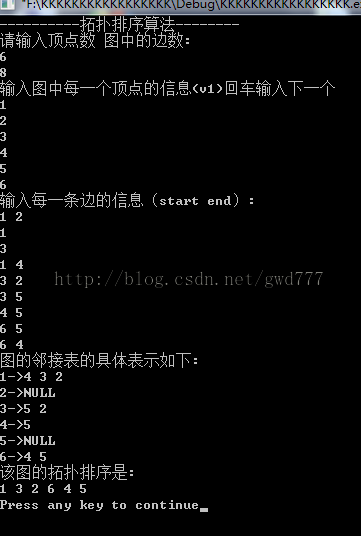
cout<<"----------拓扑排序算法--------"<<endl;
cout << "请输入顶点数 图中的边数:" <<endl;
cin >> g.vertexNum >> g.edgeNum;
cout << "输入图中每一个顶点的信息(v1)回车输入下一个" <<endl;
for (i=0;i<g.vertexNum;i++)
{
cin >> g.VertexNode[i].data; //初始化每一个顶点的mark值(vi,A,或1),每一个顶点的邻接表初始化为NULL,顶点的入度为0;
g.VertexNode[i].list = NULL;
g.VertexNode[i].indegree = 0;
}
cout << "输入每一条边的信息(start end):" <<endl;
for (j=0; j<g.edgeNum; j++)
{
cin >>edgeStart >>edgeEnd;
adjNode = new adjVertexNode;
adjNode->adjVertexPosition = edgeEnd-1; // because array begin from 0, so it is j-1
adjNode->next=g.VertexNode[edgeStart-1].list; //adjNode表示的是终止的节点,终止的节点始终指向发出线的节点
g.VertexNode[edgeStart-1].list=adjNode; //终止节点加入图中
//每增加一条边,则边的End顶点的入度加1
g.VertexNode[edgeEnd-1].indegree++;
}
}
void PrintAdjList(const Graph& g)
{
cout << "图的邻接表的具体表示如下:" << endl;
//遍历图中每一个点的邻接表(因为是一个顶点对应一个邻接表list)
for (int i=0; i < g.vertexNum; i++)
{
cout<< g.VertexNode[i].data << "->";
adjVertexNode* head = g.VertexNode[i].list;
if (head == NULL)
cout << "NULL";
while (head != NULL)
{
cout << head->adjVertexPosition + 1 <<" ";
head = head->next;
}
cout << endl;
}
}
VertexNode& FindZeroIndegree(Graph& g)
{
for (int i=0; i<g.vertexNum; i++)
{
if (g.VertexNode[i].indegree==0)
return g.VertexNode[i];
}
return g.VertexNode[0];
}
//toposort 算法
void TopSort(Graph& g)
{
cout << "该图的拓扑排序是:" <<endl;
for (int i=0; i<g.vertexNum; i++)
{
VertexNode& v = FindZeroIndegree(g);
if (v.indegree!=NULL)
cout << "该图中存在环,不能进行拓扑排序!!!"<<endl;
cout<< v.data << " ";
// for each vertex w adjacent to v, --indegree
adjVertexNode* padjv = v.list;
while (padjv!=NULL)
{//!!这个算法这里破坏了原图中的入度信息。最后入度均为1
g.VertexNode[padjv->adjVertexPosition].indegree--; //显然这里padjv记录的是每个顶点的位置信息
padjv = padjv->next;
}
//避免入度信息均为零FindZeroIndegree找到删除的顶点,将删除的顶点入度置为1
v.indegree++;
}
cout << endl;
}
/*void toppsort(Graph& g)
{
stack<VertexNode> s;
VertexNode node;
for(int i = 0;i<g.vertexNum;i++){
if(g.VertexNode[i].indegree==0)
{
s.push(g.VertexNode[i]);
}
}
while(s.empty())
{
node = s.top();
printf("%s->",node.data);
s.pop();
g.VertexNode[padjv->adjVertexPosition].indegree--;
node.list->next
}
}
*/
void DeleteGraph(Graph &g)
{
for (int i=0; i<g.vertexNum; i++)
{
adjVertexNode* tmp=NULL;
while(g.VertexNode[i].list!=NULL)
{
tmp = g.VertexNode[i].list;
g.VertexNode[i].list = g.VertexNode[i].list->next;
delete tmp;
tmp = NULL;
}
}
}
int main_toop(int argc, const char** argv)
{
Graph g;
CreateGraph(g);
PrintAdjList(g);
TopSort(g);
DeleteGraph(g);
return 0;
}
二,java版的toposort
2-1 顶点类
package 拓扑排序;
public class Vertex {
private String name;
int degree;
public int getDegree() {
return degree;
}
public void setDegree(int degree) {
this.degree = degree;
}
public Vertex(String name) {
this.name = name;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
@Override
public int hashCode() {
final int prime = 31;
int result = 1;
result = prime * result + ((name == null) ? 0 : name.hashCode());
return result;
}
@Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (getClass() != obj.getClass())
return false;
Vertex other = (Vertex) obj;
if (name == null) {
if (other.name != null)
return false;
} else if (!name.equals(other.name))
return false;
return true;
}
}
2-2 描述图的类
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;
public class Graph {
//用于存储顶点的集合Set
private Set<Vertex> vertexSet = new HashSet<Vertex>();
// 这里的hashmap相当于一个邻接表,每一个顶点都对应这一个邻接表
private Map<Vertex, Vertex[]> adjacencys = new HashMap<Vertex, Vertex[]>();
public Set<Vertex> getVertexSet() {
return vertexSet;
}
public void setVertexSet(Set<Vertex> vertexSet) {
this.vertexSet = vertexSet;
}
public Map<Vertex, Vertex[]> getAdjacencys() {
return this.adjacencys;
}
public void setAdjacencys(Map<Vertex, Vertex[]> adjacencys) {
this.adjacencys = adjacencys;
}
}
2-3 测试类
package 拓扑排序;
import java.util.ArrayList;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.Stack;
public class test {
public static Stack<Vertex> s;
public static Map<Vertex, Vertex[]> edgeMap;
public static int num = 0;
public static List<Vertex> sortList;
public static void main(String[] args) {
Graph graph = new Graph();
s = new Stack<Vertex>();
sortList = new ArrayList<Vertex>();
Set<Vertex> vertexSet = graph.getVertexSet();
num = vertexSet.size();
edgeMap = graph.getAdjacencys();
//用Java的map来构造邻接表分
Vertex oneVertex = new Vertex("1");
Vertex twoVertex = new Vertex("2");
Vertex threeVertex = new Vertex("3");
Vertex fourVertex = new Vertex("4");
Vertex fiveVertex = new Vertex("5");
Vertex sixVertex = new Vertex("6");
vertexSet.add(oneVertex);
vertexSet.add(twoVertex);
vertexSet.add(threeVertex);
vertexSet.add(fourVertex);
vertexSet.add(fiveVertex);
vertexSet.add(sixVertex);
edgeMap.put(oneVertex, new Vertex[] { twoVertex, threeVertex,fourVertex });
edgeMap.put(threeVertex, new Vertex[] { twoVertex, fiveVertex });
edgeMap.put(fourVertex, new Vertex[] { fiveVertex });
edgeMap.put(sixVertex, new Vertex[] { fourVertex, fiveVertex });
//edgeMap.put(fiveVertex, new Vertex[] { fourVertex });
// 统计节点的入读
for (Vertex vertex : vertexSet) {
Vertex[] nodeList = edgeMap.get(vertex);//map遍历的时候一定要根据K获得V
if (nodeList != null)
for (int j = 0; j < nodeList.length; j++) {
nodeList[j].degree++;
}
}
toppSort(graph);
}
public static void toppSort(Graph graph) {
Set<Vertex> vertexSet = graph.getVertexSet();
for (Vertex vertex : vertexSet) {
if (vertex.degree == 0) {
s.push(vertex);
System.out.println("入读为零的顶点:"+vertex.getName());
}
}
Vertex temp = null;
while (!s.empty()) {
temp = (Vertex) s.peek();
sortList.add(temp);
s.pop();
Vertex vertex[] = edgeMap.get(temp);
if (vertex != null)
for (int i = 0; i < vertex.length; i++) {
vertex[i].degree--;
if (vertex[i].degree == 0) {
s.push(vertex[i]);
}
}
vertexSet.remove(temp);
}
if (graph.getVertexSet().size() > num)
System.out.println("该图中有环");
else{
for(Vertex vertex:sortList){
System.out.print(vertex.getName()+"->");
}
}
}
}
三,用邻接矩阵作为数据结构的toposort,然后来求关键路径
#include <iostream>
#include <stdio.h>
using namespace std;
const int rows=6;
//用一个邻接矩阵来表示一个DAG
int length[6][6]={
{ 0, 1, 0, 0, 2, 0},
{ 0, 0, 2, 5, 0, 0},
{ 0, 0, 0, 0, 0, 5},
{ 0, 0, 0, 0, 0, 3},
{ 0, 0, 2, 0, 0, 4},
{ 0, 0, 0, 0, 0, 0},
};
//拓扑排序选出下一个点的条件:没有入度的弧;没有被访问过;不能自己遍历自己
//其实这里得到的是一个topoSort
int getNextVertex( bool *set )
//获取下一个要加入集合S的结点:它的前驱结点都在集合S内
{
for( int i=0; i<rows; i++ ){//论个扫描顶点
if( set[i] ) continue;
bool found = true;
for( int j=0; j<rows; j++ ){
if( set[j] ) continue;
if( j == i ) continue;//自己访问自己没有意义(判断条件就是筛选规则)
if( length[j][i]>0 ){//是竖着遍历一列一列的寻找,将有入度值得顶点过滤
found = false;
}
}
if( found ) {
return i;
}
}
return (-1);
}
int longestPath()
{
bool inSourceSet[rows];
for( int i=0; i<rows; i++ ){
inSourceSet[i] = false;
}
inSourceSet[0] = true;
int maxLength[rows]={0};//记录源结点到每个节点的最长路径长度
string maxPath[rows];//记录源结点到每个节点的最长路径
for( int j=1; j<rows; j++ ){
int curVex = getNextVertex( inSourceSet );
if( 0 == curVex ) continue;
cout << "->" << curVex;
int curMaxLen=0;
int preVex=0;
for( int i=0; i<rows; i++ ){//计算源结点到当前结点的最长路径长度和经过的结点并记录
if( !inSourceSet[i] ) continue;//访问过的就不再访问
//从某一列开始竖着找找到带权值的边,记录并检索谋一丁点到其他所有顶点的距离
//在入度节点里面找到最大的入度边的值,覆盖原来的值。
if( (length[i][curVex] > 0) && (curMaxLen < maxLength[i] + length[i][curVex]) ){
curMaxLen = maxLength[i] + length[i][curVex];
preVex = i;
}
}
maxLength[curVex] = curMaxLen;
inSourceSet[curVex] = true;
maxPath[curVex] = maxPath[preVex];
curMaxLen = 0;
}
return maxLength[rows-1];//返回到目标结点的最长路径
}
int main( int argc, char * argv[] )
{
int length = longestPath();
cout << "最长路径是: " << length << endl;
return (0);
}