【平衡树】【NOI 2005】维护数列
339. [NOI2005] 维护数列
★★★★☆ 输入文件:seq2005.in 输出文件:seq2005.out 简单对比
时间限制:3 s 内存限制:256 MB
【问题描述】
请写一个程序,要求维护一个数列,支持以下 6 种操作:(请注意,格式栏 中的下划线‘ _ ’表示实际输入文件中的空格)
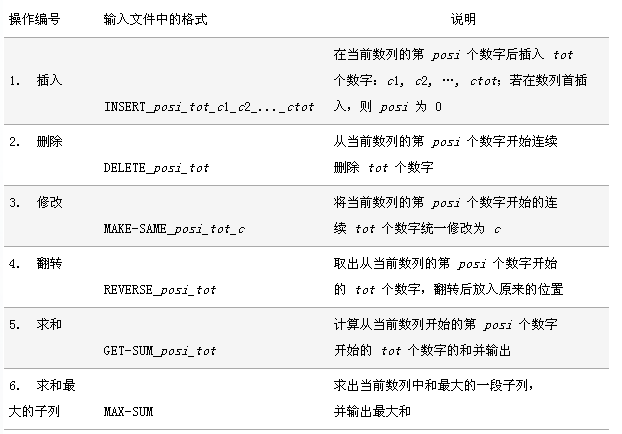
【输入格式】
输入文件的第 1 行包含两个数 N 和 M,N 表示初始时数列中数的个数,M表示要进行的操作数目。
第 2 行包含 N 个数字,描述初始时的数列。
以下 M 行,每行一条命令,格式参见问题描述中的表格。
【输出格式】
对于输入数据中的 GET-SUM 和 MAX-SUM 操作,向输出文件依次打印结果,每个答案(数字)占一行。
【输入样例】
9 8
2 -6 3 5 1 -5 -3 6 3
GET-SUM 5 4
MAX-SUM INSERT 8 3 -5 7 2
DELETE 12 1
MAKE-SAME 3 3 2
REVERSE 3 6
GET-SUM 5 4
MAX-SUM
【输出样例】
-1
10
1
10
【样例说明】
初始时,我们拥有数列 2 -6 3 5 1 -5 -3 6 3
执行操作 GET-SUM 5 4,表示求出数列中从第 5 个数开始连续 4 个数字之和,1+(-5)+(-3)+6 = -1:
2 -6 3 5 1 -5 -3 6 3
执行操作 MAX-SUM,表示要求求出当前数列中最大的一段和,应为 3+5+1+(-5)+(-3)+6+3 = 10:
2 -6 3 5 1 -5 -3 6 3
执行操作 INSERT 8 3 -5 7 2,即在数列中第 8 个数字后插入-5 7 2,
2 -6 3 5 1 -5 -3 6 -5 7 2 3
执行操作 DELETE 12 1,表示删除第 12 个数字,即最后一个:
2 -6 3 5 1 -5 -3 6 -5 7 2
执行操作 MAKE-SAME 3 3 2,表示从第 3 个数开始的 3 个数字,统一修改为 2:
2 -6 3 5 1 -5 -3 6 -5 7 2
改为
2 -6 2 2 2 -5 -3 6 -5 7 2
执行操作 REVERSE 3 6,表示取出数列中从第 3 个数开始的连续 6 个数:
2 -6 2 2 2 -5 -3 6 -5 7 2
如上所示的灰色部分 2 2 2 -5 -3 6,翻转后得到 6 -3 -5 2 2 2,并放回原来位置:
2 -6 6 -3 -5 2 2 2 -5 7 2
最后执行 GET-SUM 5 4 和 MAX-SUM,不难得到答案 1 和 10。
2 -6 6 -3 -5 2 2 2 -5 7 2
【评分方法】
本题设有部分分,对于每一个测试点:
如果你的程序能在输出文件正确的位置上打印 GET-SUM 操作的答案,你可以得到该测试点 60%的分数;
如果你的程序能在输出文件正确的位置上打印 MAX-SUM 操作的答案,你可以得到该测试点 40%的分数;
以上两条的分数可以叠加,即如果你的程序正确输出所有 GET-SUM 和MAX-SUM 操作的答案,你可以得到该测试点 100%的分数。
请注意:如果你的程序只能正确处理某一种操作,请确定在输出文件正确的位置上打印结果,即必须为另一种操作留下对应的行,否则我们不保证可以正确评分。
【数据规模和约定】
你可以认为在任何时刻,数列中至少有 1 个数。
输入数据一定是正确的,即指定位置的数在数列中一定存在。
50%的数据中,任何时刻数列中最多含有 30 000 个数;
100%的数据中,任何时刻数列中最多含有 500 000 个数。
100%的数据中,任何时刻数列中任何一个数字均在[-1 000, 1 000]内。
100%的数据中,M ≤20 000,插入的数字总数不超过 4 000 000 个,输入文件大小不超过 20MBytes。
题解:
一道十分综合的区间操作题,某神犇说1小时内写完A掉基本区间问题就可以无忧了。。然而我太弱了,写了4h+。。
每个节点需要保存的信息:
v:点权; p:键值; cnt:重复(也可以不用); sz:子树大小; sum:区间点权和;
ls:从最左边延伸出的最大连续区间和;
rs:从最右边延伸出的最大连续区间和;
maxs:整个区间的最大连续区间和;
rev:反转标记; c:修改标记;
维护:
ls=max(left->ls,left->sum+x->v+max(0,r->ls));
rs=max(right->rs,max(0,left->rs)+x->v+right->sum);
maxs=max(max(0,left->rs)+x->v+max(0,right->ls),max(left->maxs,right->maxs));
翻转交换子树和ls,rs。
具体细节注意一下就好了。
Insert:暴力插每个数。
Delete:删除区间。可以写垃圾回收。不过我懒的写了。。
Make-same:打标记,要一路下放。
Reverse:打标记,同样一路下放。
Get-sum:找到区间,直接查询即可。
Max-sum:直接查根节点maxs即可。
Code:
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define inf -0x7fffffff
using namespace std;
struct node{
node *left,*right;
int v,p,sz,cnt,sum,ls,rs,maxs,rev,c;
}*root,*null=new node((node){null,null,0,0,0,0,inf,inf,inf,inf,0,inf});
typedef pair<node*,node*> Dnode;
void push_up(node *x){
node *l=x->left,*r=x->right;
x->sz=x->cnt+l->sz+r->sz;
//sum
x->sum=x->v;
if (l->sz) x->sum+=l->sum;
if (r->sz) x->sum+=r->sum;
//ls
if (l->sz)
x->ls=max(l->ls,l->sum+x->v+max(0,r->ls));
else x->ls=max(x->v,x->v+max(0,r->ls));
//rs
if (r->sz)
x->rs=max(r->rs,max(0,l->rs)+x->v+r->sum);
else x->rs=max(x->v,x->v+max(0,l->rs));
//maxs
if (l->sz && r->sz)
x->maxs=max(0,l->rs)+x->v+max(0,r->ls);
else {
if (l->sz) x->maxs=max(l->rs,0)+x->v;
else if (r->sz) x->maxs=max(0,r->ls)+x->v;
else x->maxs=x->v;
}
if (l->sz) x->maxs=max(x->maxs,l->maxs);
if (r->sz) x->maxs=max(x->maxs,r->maxs);
x->maxs=max(x->maxs,x->sum);
}
void push_down(node *x){
node *l=x->left,*r=x->right;
if (x->c!=inf){
if (l->sz){
l->c=l->v=x->c; l->sum=l->v*l->sz;
l->ls=l->rs=l->maxs=max(l->v,l->sum);
}
if (r->sz){
r->c=r->v=x->c; r->sum=r->v*r->sz;
r->ls=r->rs=r->maxs=max(r->v,r->sum);
}
x->c=inf;
}
if (x->rev%2){
if (l->sz){
swap(l->left,l->right);
swap(l->ls,l->rs); l->rev++;
}
if (r->sz){
swap(r->left,r->right);
swap(r->ls,r->rs); r->rev++;
}
x->rev=0;
}
}
node *merge(node *x,node *y){
if (!x->sz) return y;
if (!y->sz) return x;
push_down(x); push_down(y);
if (x->p<y->p){
x->right=merge(x->right,y);
push_up(x); return x;
}
else {
y->left=merge(x,y->left);
push_up(y); return y;
}
}
Dnode split(node *x,int k){
if (!x->sz) return Dnode(null,null);
Dnode y;
push_down(x);
if (k<=x->left->sz){
y=split(x->left,k);
x->left=y.second;
push_up(x); y.second=x;
}
else {
y=split(x->right,k-x->left->sz-x->cnt);
x->right=y.first;
push_up(x); y.first=x;
}
return y;
}
void Insert(int x,int k){
Dnode y=split(root,x); node *z;
for (int i=1; i<=k; i++){
int v; scanf("%d",&v);
z=new node;
z->v=z->sum=z->ls=z->rs=z->maxs=v;
z->left=z->right=null; z->c=inf;
z->sz=z->cnt=1; z->p=rand(); z->rev=0;
y.first=merge(y.first,z);
}
root=merge(y.first,y.second);
}
void Delete(int x,int k){
Dnode y,z;
y=split(root,x-1);
z=split(y.second,k);
root=merge(y.first,z.second);
}
void Change(int x,int k,int v){
Dnode y,z;
y=split(root,x-1);
z=split(y.second,k);
z.first->c=z.first->v=v;
z.first->sum=v*z.first->sz;
z.first->ls=z.first->rs=z.first->maxs=max(v,z.first->sum);
push_down(z.first);
y.second=merge(z.first,z.second);
root=merge(y.first,y.second);
}
void Reverse(int x,int k){
Dnode y,z;
y=split(root,x-1);
z=split(y.second,k);
z.first->rev++;
swap(z.first->left,z.first->right);
swap(z.first->ls,z.first->rs);
push_down(z.first);
y.second=merge(z.first,z.second);
root=merge(y.first,y.second);
}
void Q_sum(int x,int k){
Dnode y,z;
if (!k){
printf("0\n");
return;
}
y=split(root,x-1);
z=split(y.second,k);
push_up(z.first);
printf("%d\n",z.first->sum);
y.second=merge(z.first,z.second);
root=merge(y.first,y.second);
}
int main(){
int n,m; root=null; char opt[20]; scanf("%d%d",&n,&m); Insert(0,n); while (m--){ scanf("%s",&opt); int x,y,z; switch (opt[0]){ case 'I':scanf("%d%d",&x,&y); Insert(x,y); break; case 'D':scanf("%d%d",&x,&y); Delete(x,y); break; case 'M':{ if (opt[2]=='K') scanf("%d%d%d",&x,&y,&z),Change(x,y,z); else printf("%d\n",root->maxs); break; } case 'R':scanf("%d%d",&x,&y); Reverse(x,y); break; case 'G':scanf("%d%d",&x,&y); Q_sum(x,y); break; } // cout<<root->v<<" "<<root->p<<" "<<root->sz<<" "<<root->sum<<" "<<root->ls<<" "<<root->rs<<" "<<root->maxs<<endl; } return 0; }