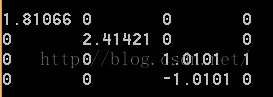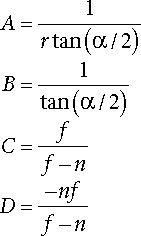龙书D3D11章节习题答案(第五章)
以下答案仅供参考,有错欢迎讨论。
Chapter 5:The Rendering Pipeline
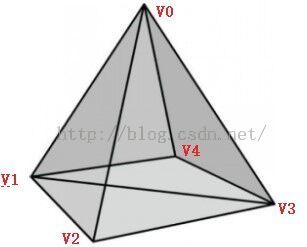
1. Construct the vertex and index list of a pyramid(金字塔), as shown in Figure 5.35(即下图).
Vertex pyramid[5] = {v0, v1, v2, v3, v4, v5};
// 注意要从面的outside看向inside,然后按照顺时针绕序,如下
UINT indexList[6] = { 0, 1, 4,
0, 3, 2,
0, 4, 3,
0, 2, 1,
3, 4, 1,
3, 1, 2};
这里我用dx9绘制了一下来验证结果:
1.为了方便观察金字塔全貌,让绘制出的金字塔绕x轴向上翻转45°,并绕y轴不停旋转。
2.设置CULLMODE为D3DCULL_NONE,观察到所有顶点及其连线。
理由:默认的背面剔除方式是剔除逆时针绕序的三角形,即D3DCULL_CCW (Couter-Clock-Wise)。
而在这种方式下,因为旋转中的金字塔底部对于我们的视角(摄像机镜头)来说,一会是正面(绘制)一会是反面(不绘制)。
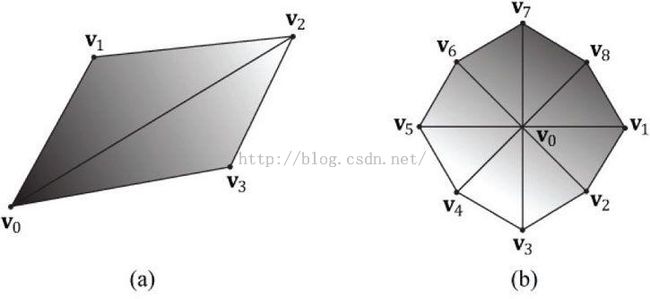
2. Consider the two shapes shown in Figure 5.36(即下图). Merge the objects into one vertex and index list. (The idea here is that when you append the 2nd index list to the first, you will need to update the appended indices since they reference vertices in the original vertex list, not the merged vertex list.)
这道题的意思似乎是把绘制a和b所用到的vertex list和index list合起来写。。定义v0,v1,...,v12,v13,慢慢写索引不就行了。。也许是我没悟到题目的意思...
3. Relative to the world coordinate system, suppose that the camera is positioned at (−20, 35, −50) and looking at the point (10, 0, 30). Compute the view matrix assuming (0, 1, 0) describes the “up” direction in the world.
这题是关于ViewMatrix推导的。
View Transform(视图变换)详解
【D3D11游戏编程】学习笔记二十:第一人称摄像机的实现
条件:EyePosition(-20,35,-50), FocusPosition(10,0,30), UpDirection(0,1,0)
#include <iostream>
#include <windows.h> // FLOAT
#include <xnamath.h>
using namespace std;
// Overload the "<<" operators so that we can use cout to
// output XMVECTOR and XMMATRIX objects.
ostream& operator<<(ostream& os, FXMVECTOR v)
{
XMFLOAT4 dest;
XMStoreFloat4(&dest, v);
os << "(" << dest.x << ", " << dest.y << ", " << dest.z << ", " << dest.w << ")";
return os;
}
ostream& operator<<(ostream& os, CXMMATRIX m)
{
for(int i = 0; i < 4; ++i)
{
for(int j = 0; j < 4; ++j)
os << m(i, j) << "\t";
os << endl;
}
return os;
}
// 把条件代入XNMATH提供的XMMatrixLookAtLH函数里面计算结果,然后再根据自己推导的步骤计算,若结果相同,则推导正确。
int main()
{
// Check support for SSE2 (Pentium4, AMD K8, and above).
if( !XMVerifyCPUSupport() )
{
cout << "xna math not supported" << endl;
return 0;
}
XMVECTOR pos = XMVectorSet(-25.0f, 35.0f, -50.0f, 1.0f);
XMVECTOR target = XMVectorSet(10.0f, 0.0f, 30.0f, 1.0f);
XMVECTOR up = XMVectorSet(0.0f, 1.0f, 0.0f, 0.0f);
XMMATRIX view = XMMatrixLookAtLH(pos, target, up);
cout.precision(4);
cout << endl << view << endl;
// direction
XMVECTOR d = target - pos;
d = XMVector3Normalize(d);
cout << "d = "<< d << endl;
// right
XMVECTOR r = XMVector3Cross(up, d);
r = XMVector3Normalize(r);
cout << "r = "<< r << endl;
// up
XMVECTOR u = XMVector3Cross(d, r);
cout << "u = "<< u << endl;
float x = -XMVectorGetY(XMVector3Dot(pos,r));
float y = -XMVectorGetY(XMVector3Dot(pos,u));
float z = -XMVectorGetY(XMVector3Dot(pos,d));
XMMATRIX M;
M(0,0) = r.m128_f32[0]; // r.x
M(1,0) = r.m128_f32[1]; // r.y
M(2,0) = r.m128_f32[2]; // r.z
M(3,0) = x;
M(0,1) = u.m128_f32[0];
M(1,1) = u.m128_f32[1];
M(2,1) = u.m128_f32[2];
M(3,1) = y;
M(0,2) = d.m128_f32[0];
M(1,2) = d.m128_f32[1];
M(2,2) = d.m128_f32[2];
M(3,2) = z;
M(0,3) = 0.0f;
M(1,3) = 0.0f;
M(2,3) = 0.0f;
M(3,3) = 1.0f;
cout << endl << M <<endl;
return 0;
}
对XMVector3Dot返回的是XMVECTOR感到很奇怪。。
Return value
Returns a vector. The dot product between V1 and V2 is replicated into each component.
不过不妨碍我们使用它,根据解释,对返回的XMVECTOR调用XMVectorGetX、XMVectorGetY、XMVectorGetZ都可以取到想要的点积的值。
4. Given that the view frustum has a vertical field of view angle θ = 45°, the aspect ratio is a = 4/3, the near plane is n = 1, and the far plane is f = 100, find the corresponding perspective projection matrix.
这题是关于Perspective Matrix的。
A = 1/(a*tan(θ/2) = 1.81066;
B = 1/(tan(θ/2) = 2.41421;
C = f/(f-n) = 1.0101;
D = -nf/(f-n) = -1.0101;
透视投影详解
深入探索透视投影变换
深入探索透视投影变换(续)
关于投影平面变换到viewport后多边形的失真问题
5. Suppose that the view window has height 4. Find the distance d from the origin the view window must be to create a vertical field of view angle θ = 60°.
已知h/2 = 2, θ/2 = 30°,(h/2)/d = tan(θ/2) , 故d = 2根号3。
6. Consider the following perspective projection matrix:

Find the vertical field of view angle α, the aspect ratio r, and the near and far plane values that were used to build this matrix.
1/(tan(θ/2) = 3.73205 ---> θ = 30°
1.86603 = 1/2 *3.73205 ---> r = 2
-5.12821/1.02564 = -5 ---> n = 5
f/(f-n) = 1.02564 ---> f = 200
7. Suppose that you are given the following perspective projection matrix with fixed A, B, C, D:
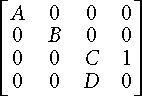
Find the vertical field of view angle a, the aspect ratio r, and the near and far plane values that were used to build this matrix in terms of A, B, C, D.That is, solve the following equations:
Solving these equations will give you formulas for extracting the vertical field of view angle α, the aspect ratio r, and the near and far plane values from any perspective projection matrix of the kind described in this book.
r = B/A;
α = 2 * arctan(1/B);
n = - D/C;
f = n/(1 - 1/C);
8. For projective texturing algorithms, we multiply an affine(仿射) transformation matrix T after the projection matrix. Prove that it does not matter if we do the perspective divide before or after multiplying by T. Let v be a 4D vector, P be a projection matrix, T be a 4 × 4 affine transformation matrix, and let a w subscript(下标) denote the w-coordinate of a 4D vector, and prove:
证明就略过了,仿射变换包括旋转、缩放、平移等变换,我分别把这三种仿射矩阵代入T当中运算,等式成立。
9. Prove that the inverse of the projection matrix is given by:
代入A、B、C、D之后,所得矩阵正好与题目所给的矩阵相同。
10. Let [x, y, z, 1] be the coordinates of a point in view space, and let [xndc, yndc, zndc, 1] be the coordinates of the same point in NDC space. Prove that you can transform from NDC space to view space in the following way:
Explain why you need the division by w. Would you need the division by w if you were transforming from homogeneous clip space to view space?
使用第九题的 p 和 p逆 计算一下即可证明上式。
(x, y, z, 1) * p = (Ax, By, Cz+D, z) = (Ax/z, By/z, C+D/z, 1),即[xndc, yndc, zndc, 1] = (Ax/z, By/z, C+D/z, 1);
(Ax/z, By/z, C+D/z, 1) * p逆 = (x/z, y/z, 1, 1/z) = (x, y, z, 1);
为什么需要除以w,是要让经过变换后的四维坐标的w分量与变换前的四维坐标的w分量相同,即两个坐标点表示处在同一个三维空间中( 就像14题的结论(a)描述的 )。
需要,理由同上。
11. Another way to describe the view frustum is by specifying the width and height of the view volume at the near plane. Given the width w and height h of the view volume at the near plane, and given the near plane n and far plane f, show that the perspective projection matrix is given by:
Figure 5.37. The x- and y-coordinates sheared by the z-coordinate. The top face of the box lies in the z = 1 plane. Observe that the shear transform translates points in this plane.
1/( (w/h)*( (h/2) / n ) ) = 2n/w
1/( (h/2) / n ) = 2n/h
12. Given a view frustum with vertical field of view angle θ, aspect ratio a, near plane n, and far plane f, find the 8 vertex corners of the frustum.
(h/2) / n = tan(θ/2)
h = 2n*tan(θ/2)
w = a*2n*tan(θ/2)
近平面的四个顶点(±w/2, ±h/2, n, 1), 代入w、h
n/f = (±w/2)/x = (±h/2)/y
远平面的四个顶点(±wf/2n, fh/2n, f, 1), 代入w、h
13. Consider the 3D shear transform given by Sxy (x, y, z) = (x + ztx, y + zty, z). This transformation is illustrated in Figure 5.37. Prove that this is a linear transformation and has the following matrix representation:
变换的方式只是根据z坐标值的大小,或多或少地把原坐标点向+x,+y轴各自移动一段距离,变换显然是线性的。
(x, y, z) * Sxy = (x + ztx, y + zty, z)
14. Consider 3D points in the plane z = 1; that is, points of the form (x, y, 1). Observe that transforming a point (x, y, 1) by the shear transformation Sxy given in the previous exercise amounts to a 2D translation in the z = 1 plane:
If we are working on a 2D application, we could use 3D coordinates, but where our 2D universe always lies on the plane z = 1; then we could use Sxy to do translations in our 2D space.
Conclude the following generalizations:
(a) Just as a plane in 3D space is a 2D space, a plane in 4D space is a 3D space. When we write homogeneous points (x, y, z, 1) we are working in the 3D space that lives in the 4D plane w = 1.
(b) The translation matrix is the matrix representation of the 4D shear transformation Sxyz(x, y, z, w) = (x + wtx, y + wty, z + wtz, w). The 4D shear transformation has the effect of translating points in the plane w = 1.
读了两遍,说的很有道理,但没找到题目是什么。。