后缀数组-解决字符串的利器

关于后缀数组的详细介绍，可见另一篇转载过来的介绍：

http://blog.csdn.net/slime_kirito/article/details/49050043

本文主要是对于实际问题的代码实现

后缀数组是解决部分字符串问题的利器。

主要是运用height数组，Suff数组(SA数组)

对于求以上数组的模板：

#include<iostream>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 100;
int height[MAXN];
string Suff[MAXN];
bool cmp(string a, string b)//比较函数
{
	return a < b;
}
//最长公共前缀
int Comlen_Suff(string s1, string s2)
{
	int p = 0, q = 0;
	int len = 0;
	while (p != s1.length() && q != s2.length() && s1[p++] == s2[q++])
	{
		++len;
	}
	return len;
}
void Make(string s)
{
	int len = s.length();
	memset(height, 0, sizeof(height));
	for (int i = 0; i < len; i++)
	{
		Suff[i] = &s[i];
	}
	sort(Suff, Suff + len, cmp);
	/*for (int i = 0; i < len; i++)
	{
		cout << Suff[i] << endl;
	}*/
	for (int i = 0; i < len - 1; i++)
	{
		height[i] = Comlen_Suff(Suff[i], Suff[i + 1]);
	}
	/*for (int i = 0; i < len - 1; i++)
	{
		cout << height[i] << endl;
	}*/
}

后缀数组应用

① 单个字符串相关问题

1 可重叠最长重复子串（LRS）

给定一个字符串，求最长重复子串，这两个子串可以重叠。

『解析』只需要求height 数组里的最大值即可。

#include<iostream>
#include<string>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 100;
bool cmp(string a, string b)//比较函数
{
	return a < b;
}
//最长公共前缀
int Comlen_Suff(string s1, string s2)
{
	int p = 0, q = 0;
	int len = 0;
	while (p != s1.length() && q != s2.length() && s1[p++] == s2[q++])
	{
		++len;
	}
	return len;
}
void LRS(string s)
{
	string Suff[MAXN];
	int len = s.length(),maxlen = 0,maxi=0;
	for (int i = 0; i < len; i++)
	{
		Suff[i] = &s[i];
	}
	sort(Suff, Suff + len, cmp);
	for (int i = 0; i < len - 1; i++)
	{
		int len = Comlen_Suff(Suff[i], Suff[i + 1]);
		if (len > maxlen)
		{
			maxlen = len;
			maxi = i;
		}
	}
	cout << "最长重复子串的长度为：" << maxlen << endl;;
	cout << "该串为：" << Suff[maxi] << endl;
}

2 不可重叠最长重复子串

给定一个字符串，求最长重复子串，这两个子串不能重叠。

对这个字符串构造后缀数组，在每个后缀数组中，寻找没有重复字符的最长前缀，就是要找的子串。

#include<iostream>
#include<string>
#include<cstring>
using namespace std;
const int MAXN = 10000;
//得到字符串最长的无重复的前缀长度
int longestlen(char * p)
{
	int vis[MAXN];//MAXN要多开一些空间
	int len = 0;
	memset(vis, 0, sizeof(vis));
	while (*p && !vis[*p])
	{
		vis[*p] = 1;
		++len;
		++p;
	}
	return len;
}

//使用后缀数组解法
void longest_unique_substring(char * str)
{
	int maxlen = -1, maxi = 0;
	char *Suff[MAXN];//MAXN要多开一些空间
	int n = 0;
	while (*str != '\0')
	{
		Suff[n++] = str++;
	}
	for (int i = 0; i<n; i++)
	{
		int len = longestlen(Suff[i]);
		if (len > maxlen)
		{
			maxlen = len;
			maxi = i;
		}
	}
	printf("最长的无重复的前缀长度为%d:\n", maxlen);
	printf("该串为:");
	printf("%.*s\n", maxlen, Suff[maxi]);
	//%.*s:从maxi开始连续manlen个字符
}

3 可重叠的k 次最长重复子串

给定一个字符串，求至少出现k 次的最长重复子串，这k 个子串可以重叠。

『解析』 先二分答案，然后将后缀分成若干组。不同的是，这里要判断的是有没有一个组的后缀个数不小于k。如果有，那么存在k 个相同的子串满足条件，否则不存在。这个做法的时间复杂度为O(nlogn)。

(未)

4 后缀数组求最长回文子串（LPS）

给定一个字符串，求最长回文子串。

『解析』 将整个字符串反过来写在原字符串后面，中间用一个特殊的字符隔开。

  这样就把问题变为了求这个新的字符串的某两个后缀的最长公共前缀。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
const int MAXN = 1000;
//用于sort的比较函数
bool cmp(string a, string b)
{
	return a < b;
}
//最长公共前缀
int comlen_suff(string s1, string s2)
{
	int p = 0, q = 0;
	int len = 0;
	int count = 0; //保证两个子串中只有一个含有‘#’，LCS才来自两个字符串，否则可能来自同一个字符串
	while (p != s1.length() && q != s2.length() && s1[p++] == s2[q++])
	{
		++len;
		if (s1[p] == '#' || s2[q] == '#')
		{
			break;
		}
	}
	while (p != s1.length())
	{
		if (s1[p++] == '#')
		{
			++count;
			break;
		}
	}
	while (q != s2.length())
	{
		if (s2[q++] == '#')
		{
			++count;
			break;
		}
	}
	if (count == 1)
		return len;
	return 0;
}

//最长公共子串
void LCS(string s)
{
	int maxlen = 0;
	int suf_index;
	int len_suff = s.length()*2 + 1;
	string suff[MAXN], arr; // 将X和Y连接到一起
	arr += s;
	arr += '#';
	for (int i = s.length() - 1; i >= 0; i--)
	{
		arr += s[i];
	}
	arr += '\0';
	for (int i = 0; i < len_suff; ++i)  // 初始化后缀数组
	{
		suff[i] = &arr[i];
	}
	sort(suff, suff + len_suff, cmp);
	for (int i = 0; i < len_suff - 1; ++i)
	{
		int len = comlen_suff(suff[i], suff[i + 1]);
		if (len > maxlen)
		{
			maxlen = len;
			suf_index = i;
		}
	}
	cout << "LCS长度为：" << maxlen << endl;
	cout << "该串为:" << suff[suf_index] << endl;
}

5 连续重复子串

给定一个字符串L，已知这个字符串是由某个字符串S 重复R 次而得到的，求R 的最大值。

『解析』穷举字符串S 的长度k，然后判断是否满足。判断的时候，先看字符串L 的长度能否被k 整除，再看suffix(1)和suffix(k+1)的最长公共前缀是否等于n-k。在询问最长公共前缀的时候，suffix(1)是固定的，所以RMQ问题没有必要做所有的预处理， 只需求出height 数组中的每一个数到height[rank[1]]之间的最小值即可。整个做法的时间复杂度为O(n)。

(未)

6 重复次数最多的连续重复子串

给定一个字符串，求重复次数最多的连续重复子串。

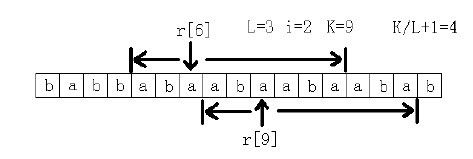
『解析』先穷举长度L，然后求长度为L 的子串最多能连续出现几次。首先连续出现1 次是肯定可以的，所以这里只考虑至少2 次的情况。假设在原字符串中连续出现2 次，记这个子字符串为S，那么S 肯定包括了字符r[0], r[L], r[L*2],r[L*3], ……中的某相邻的两个。所以只须看字符r[L*i]和r[L*(i+1)]往前和往后各能匹配到多远，记这个总长度为K，那么这里连续出现了K/L+1 次。最后看最大值是多少。

穷举长度L 的时间是n，每次计算的时间是n/L。所以整个做法的时间复杂度是O(n/1+n/2+n/3+……+n/n)=O(nlogn)。

(未)

②  两个字符串相关问题

1 后缀数组求最长公共子串（LCS）

解法：将两个字符串用一个特殊符号（两个字符串中都没有，比如‘#’）连接起来，
构造连接后字符串的后缀数组，求后缀数组中的最长公共前缀，要保证最长的公共前
缀在原来两个字符串中都出现，而不是只出现在一个字符串中，这就是特殊连接符号
的作用。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
using namespace std;
const int MAXN = 1000;
//用于sort的比较函数
bool cmp(string a, string b)
{
	return a < b;
}

//最长公共前缀
int comlen_suff(string s1,string s2)
{
	int p=0, q=0;
	int len = 0;
	int count = 0; //保证两个子串中只有一个含有‘#’，LCS才来自两个字符串，否则可能来自同一个字符串
	while (p!=s1.length() && q!=s2.length() && s1[p++] == s2[q++])
	{
		++len;
		if (s1[p] == '#' || s2[q] == '#')
		{
			break;
		}
	}
	while (p!=s1.length())
	{
		if (s1[p++] == '#')
		{
			++count;
			break;
		}
	}
	while (q!=s2.length())
	{
		if (s2[q++] == '#')
		{
			++count;
			break;
		}
	}
	if (count == 1)
		return len;
	return 0;
}

//最长公共子串
void LCS(string s1,string s2)
{
	int maxlen = 0;
	int suf_index;
	int len_suff = s1.length()+s2.length() + 1;
	string suff[MAXN], arr; // 将X和Y连接到一起
	arr += s1;
	arr += '#';
	arr += s2;
	arr += '\0';
	for (int i = 0; i < len_suff; ++i)  // 初始化后缀数组
	{
		suff[i] = &arr[i];
	}
	sort(suff, suff+len_suff, cmp);
	for (int i = 0; i < len_suff - 1; ++i)
	{
		int len = comlen_suff(suff[i], suff[i + 1]);
		if (len > maxlen)
		{
			maxlen = len;
			suf_index = i;
		}
	}
	cout << "LCS长度为：" << maxlen << endl;
	cout << "该串为:" << suff[suf_index]<<endl;
}

2 长度不小于k 的公共子串的个数

给定两个字符串A 和B，求长度不小于k 的公共子串的个数（可以相同）。

『解析』基本思路是计算A 的所有后缀和B 的所有后缀之间的最长公共前缀的长度，把最长公共前缀长度不小于k 的部分全部加起来。先将两个字符串连起来，中间用一个没有出现过的字符隔开。按height 值分组后，接下来的工作便是快速的统计每组中后缀之间的最长公共前缀之和。扫描一遍，每遇到一个B 的后缀就统计与前面的A 的后缀能产生多少个长度不小于k 的公共子串，这里A 的后缀需要用一个单调的栈来高效的维护。然后对A 也这样做一次。

（未）

③ 多个字符串相关问题

1 不小于k 个字符串中的最长子串

给定n 个字符串，求出现在不小于k 个字符串中的最长子串。

『解析』将n 个字符串连起来，中间用不相同的且没有出现在字符串中的字符隔开，求后缀数组。然后二分答案：将后缀分成若干组，判断每组的后缀是否出现在不小于k 个的原串中。这个做法的时间复杂度为O(nlogn)。

(未)

2 每个字符串至少出现两次且不重叠的最长子串

给定n 个字符串，求在每个字符串中至少出现两次且不重叠的最长子串。

『解析』做法和上题大同小异，也是先将n 个字符串连起来，中间用不相同的且没有出现在字符串中的字符隔开，求后缀数组。然后二分答案，再将后缀分组。判断的时候，要看是否有一组后缀在每个原来的字符串中至少出现两次，并且在每个原来的字符串中，后缀的起始位置的最大值与最小值之差是否不小于当前答案（判断能否做到不重叠，如果题目中没有不重叠的要求，那么不用做此判断）。这个做法的时间复杂度为O(nlogn)。

（未）

3 出现或反转后出现在每个字符串中的最长子串

给定n 个字符串，求出现或反转后出现在每个字符串中的最长子串。

『解析』这题不同的地方在于要判断是否在反转后的字符串中出现。其实这并没有加大题目的难度。只需要先将每个字符串都反过来写一遍，中间用一个互不相同的且没有出现在字符串中的字符隔开，再将n 个字符串全部连起来，中间也是用一个互不相同的且没有出现在字符串中的字符隔开，求后缀数组。然后二分答案，再将后缀分组。判断的时候，要看是否有一组后缀在每个原来的字符串或反转后的字符串中出现。这个做法的时间复杂度为O(nlogn)。

(未)

总结
后缀数组实际上可以看作后缀树的所有叶结点按照从左到右的次序排列放入数组中形成的，所以后缀数组的用途不可能超出后缀树的范围。甚至可以说，如果不配合【最长公共前缀】函数，后缀数组的应用范围是很狭窄的。但是有【最长公共前缀】 函数配合下的后缀数组就非常强大，可以完成大多数后缀树所能完成的任务，因为这个【最长公共前缀】函数实际上给出了任意两个叶子结点的最近公共祖先，这方面的内容大家可以自行研究。