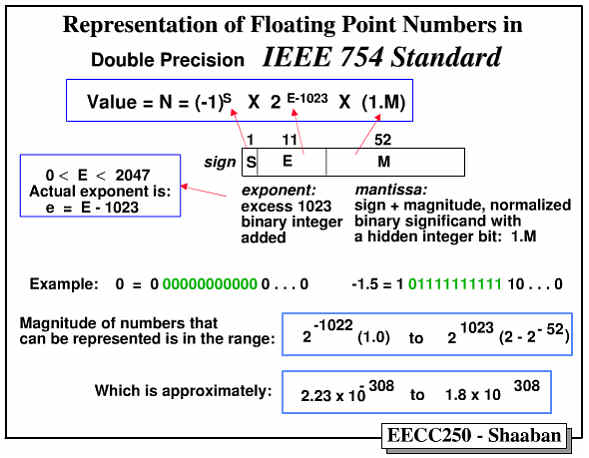
浮点数的二进制表示

1. 单精度浮点型

目前单精度浮点数float为32位。
S: 1bit, 符号位
    0表示该float为正数, 1表示为负数

E: 指数, 8bits
    E - 127 = e 实际的指数

M: 尾数, 23位
    一个实数在存储之前，总是先格式为"规范化形式", 即1.XXX格式, 然后把XXX部分存储（M）。
   由于其格式固定，在小数点前固定为一个1，所以小数点前的部分是不用保存的。

   例如:
     0.5
     = 0. 1000 0000 (B)
     = 1.0000 0000 (B) * 2^(-1)  规范化为1.XXX格式
     其中, M部分就是 0000 0000，
             指数e=-1，E = e + 127 = 126
             float的二进制表示  0, 0111 1110, 0000 0000 0000 0000 0000 000
            
      2.5
      = 0010 . 1000 0000 B
      = 1. 0100 0000 0000 B * 2^1
     其中, M =  0100 0000
              e=1,  E = e + 127 = 128
              float二进制表示为 0, 1000 0000, 0100 0000 0000 0000 0000 000

       注: 0的表示比较特别, 0的规范化形式为 1. 0 * 2^(-127), 即0不是0，而是 1 / 2^127。
      S = 0
      E = -127 + 127 = 0
      M = 0000 0000
     所以0的float的二进制表示为 0, 0000 0000, 0000 0000 0000 0000 000

   

 
大小端
按照上述表示, 符号位S是最高位。因此，把符号位所在字节放在前面的称为Little-Endian，
把符号为放在后面的为Big-Endian。
例如:
2.5 ( 0, 1000 0000, 0100 0000 0000 0000 0000 000) (重排序: 0100 0000 0010 0000 0 0000 0000 0000 000
= 40 20 00 00 (Big-Endian)
= 00 00 20 40
    

2. 双精度浮点