十六、图算法之有向图
有向图
有向图的数据结构
采用链表
public class Digraph {
private static final String NEWLINE = System.getProperty("line.separator");
private final int V; // number of vertices in this digraph
private int E; // number of edges in this digraph
private Bag<Integer>[] adj; // adj[v] = adjacency list for vertex v
private int[] indegree; // indegree[v] = indegree of vertex v
public Digraph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
this.V = V;
this.E = 0;
indegree = new int[V];
adj = (Bag<Integer>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Integer>();
}
}
public Digraph(In in) {
try {
this.V = in.readInt();
if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
indegree = new int[V];
adj = (Bag<Integer>[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Integer>();
}
int E = in.readInt();
if (E < 0) throw new IllegalArgumentException("Number of edges in a Digraph must be nonnegative");
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
addEdge(v, w);
}
}
catch (NoSuchElementException e) {
throw new InputMismatchException("Invalid input format in Digraph constructor");
}
}
public Digraph(Digraph G) {
this(G.V());
this.E = G.E();
for (int v = 0; v < V; v++)
this.indegree[v] = G.indegree(v);
for (int v = 0; v < G.V(); v++) {
// reverse so that adjacency list is in same order as original
Stack<Integer> reverse = new Stack<Integer>();
for (int w : G.adj[v]) {
reverse.push(w);
}
for (int w : reverse) {
adj[v].add(w);
}
}
}
public int V() {
return V;
}
public int E() {
return E;
}
// throw an IndexOutOfBoundsException unless 0 <= v < V
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IndexOutOfBoundsException("vertex " + v + " is not between 0 and " + (V-1));
}
public void addEdge(int v, int w) {
validateVertex(v);
validateVertex(w);
adj[v].add(w);
indegree[w]++;
E++;
}
public Iterable<Integer> adj(int v) {
validateVertex(v);
return adj[v];
}
public int outdegree(int v) {
validateVertex(v);
return adj[v].size();
}
public int indegree(int v) {
validateVertex(v);
return indegree[v];
}
public Digraph reverse() {
Digraph R = new Digraph(V);
for (int v = 0; v < V; v++) {
for (int w : adj(v)) {
R.addEdge(w, v);
}
}
return R;
}
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " vertices, " + E + " edges " + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(String.format("%d: ", v));
for (int w : adj[v]) {
s.append(String.format("%d ", w));
}
s.append(NEWLINE);
}
return s.toString();
}
}有向图的可达性(采用深度优先搜索)
两种构造函数分别针对单源可达性和多源可达性
public class DirectedDFS {
private boolean[] marked; // marked[v] = true if v is reachable
// from source (or sources)
private int count; // number of vertices reachable from s
public DirectedDFS(Digraph G, int s) {
marked = new boolean[G.V()];
dfs(G, s);
}
public DirectedDFS(Digraph G, Iterable<Integer> sources) {
marked = new boolean[G.V()];
for (int v : sources) {
if (!marked[v]) dfs(G, v);
}
}
private void dfs(Digraph G, int v) {
count++;
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) dfs(G, w);
}
}
public boolean marked(int v) {
return marked[v];
}
public int count() {
return count;
}
}有向图中检测环
public class DirectedCycle {
private boolean[] marked; // marked[v] = has vertex v been marked?
private int[] edgeTo; // edgeTo[v] = previous vertex on path to v
private boolean[] onStack; // onStack[v] = is vertex on the stack?
private Stack<Integer> cycle; // directed cycle (or null if no such cycle)
public DirectedCycle(Digraph G) {
marked = new boolean[G.V()];
onStack = new boolean[G.V()];
edgeTo = new int[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v] && cycle == null) dfs(G, v);
}
// check that algorithm computes either the topological order or finds a directed cycle
private void dfs(Digraph G, int v) {
onStack[v] = true;
marked[v] = true;
for (int w : G.adj(v)) {
// short circuit if directed cycle found
if (cycle != null) return;
//found new vertex, so recur
else if (!marked[w]) {
edgeTo[w] = v;
dfs(G, w);
}
// trace back directed cycle
else if (onStack[w]) {
cycle = new Stack<Integer>();
for (int x = v; x != w; x = edgeTo[x]) {
cycle.push(x);
}
cycle.push(w);
cycle.push(v);
assert check();
}
}
onStack[v] = false;
}
public boolean hasCycle() {
return cycle != null;
}
public Iterable<Integer> cycle() {
return cycle;
}
// certify that digraph has a directed cycle if it reports one
private boolean check() {
if (hasCycle()) {
// verify cycle
int first = -1, last = -1;
for (int v : cycle()) {
if (first == -1) first = v;
last = v;
}
if (first != last) {
System.err.printf("cycle begins with %d and ends with %d\n", first, last);
return false;
}
}
return true;
}
}拓扑排序
给定一个有向图,将所有的顶点排序,使得所有的有向边均是从前面的元素指向排在后面的元素(序列前后某两点并不一定是连通的,但是连通的每条边都是从前面某点指向这个序列的后面某点)。
当且仅当一幅有向图是无环图时它才能进行拓扑排序(有环就分不清前后了,还排什么序)
基于深度优先搜索的顶点排序(不是拓扑排序,十分重要)
先学习顶点排序:这里面有preourder,postorder和reverse postorder
preorder也叫前序,是dfs调用的顺序(每次调用先给你加入队列,追踪dfs的调用顺序)
postorder也叫后序,是顶点遍历完成后(先走到尽头或者说先完成dfs(那个for结束了))的顺序
reverse postorder也叫逆后序,就是后序倒过来
public class DepthFirstOrder {
private boolean[] marked; // marked[v] = has v been marked in dfs?
private int[] pre; // pre[v] = preorder number of v
private int[] post; // post[v] = postorder number of v
private Queue<Integer> preorder; // vertices in preorder
private Queue<Integer> postorder; // vertices in postorder
private int preCounter; // counter or preorder numbering
private int postCounter; // counter for postorder numbering
public DepthFirstOrder(Digraph G) {
pre = new int[G.V()];
post = new int[G.V()];
postorder = new Queue<Integer>();
preorder = new Queue<Integer>();
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v]) dfs(G, v);
}
public DepthFirstOrder(EdgeWeightedDigraph G) {
pre = new int[G.V()];
post = new int[G.V()];
postorder = new Queue<Integer>();
preorder = new Queue<Integer>();
marked = new boolean[G.V()];
for (int v = 0; v < G.V(); v++)
if (!marked[v]) dfs(G, v);
}
// run DFS in digraph G from vertex v and compute preorder/postorder
private void dfs(Digraph G, int v) {
marked[v] = true;
pre[v] = preCounter++;
preorder.enqueue(v);
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
postorder.enqueue(v);
post[v] = postCounter++;
}
// run DFS in edge-weighted digraph G from vertex v and compute preorder/postorder
private void dfs(EdgeWeightedDigraph G, int v) {
marked[v] = true;
pre[v] = preCounter++;
preorder.enqueue(v);
for (DirectedEdge e : G.adj(v)) {
int w = e.to();
if (!marked[w]) {
dfs(G, w);
}
}
postorder.enqueue(v);
post[v] = postCounter++;
}
public int pre(int v) {
return pre[v];
}
public int post(int v) {
return post[v];
}
public Iterable<Integer> post() {
return postorder;
}
public Iterable<Integer> pre() {
return preorder;
}
public Iterable<Integer> reversePost() {
Stack<Integer> reverse = new Stack<Integer>();
for (int v : postorder)
reverse.push(v);
return reverse;
}
// check that pre() and post() are consistent with pre(v) and post(v)
private boolean check(Digraph G) {
// check that post(v) is consistent with post()
int r = 0;
for (int v : post()) {
if (post(v) != r) {
StdOut.println("post(v) and post() inconsistent");
return false;
}
r++;
}
// check that pre(v) is consistent with pre()
r = 0;
for (int v : pre()) {
if (pre(v) != r) {
StdOut.println("pre(v) and pre() inconsistent");
return false;
}
r++;
}
return true;
}
}拓扑排序
顶点排序的逆后序就是拓扑排序(因为顶点后序中的点是先完成dfs(或者叫先走到尽头)的点排在前面,在dfs每到尽头回溯的过程中,排在前面的点(走到尽头)肯定能被排在后面的(往回 回溯的)某些点访问到,所以倒过来,这个肯定能被访问到的点就放在拓扑排序的靠后面了,相当于拓扑排序把后序倒了过来)

内部就是使用了DepthFirstOrder
public class Topological {
private Iterable<Integer> order; // topological order
private int[] rank; // rank[v] = position of vertex v in topological order
public Topological(Digraph G) {
DirectedCycle finder = new DirectedCycle(G);
if (!finder.hasCycle()) {
DepthFirstOrder dfs = new DepthFirstOrder(G);
order = dfs.reversePost();
rank = new int[G.V()];
int i = 0;
for (int v : order)
rank[v] = i++;
}
}
public Topological(EdgeWeightedDigraph G) {
EdgeWeightedDirectedCycle finder = new EdgeWeightedDirectedCycle(G);
if (!finder.hasCycle()) {
DepthFirstOrder dfs = new DepthFirstOrder(G);
order = dfs.reversePost();
}
}
public Iterable<Integer> order() {
return order;
}
public boolean hasOrder() {
return order != null;
}
public int rank(int v) {
validateVertex(v);
if (hasOrder()) return rank[v];
else return -1;
}
// throw an IndexOutOfBoundsException unless 0 <= v < V
private void validateVertex(int v) {
int V = rank.length;
if (v < 0 || v >= V)
throw new IndexOutOfBoundsException("vertex " + v + " is not between 0 and " + (V-1));
}
}有向图中的强连通性
强连通: 如果两个顶点v和w是互相可达的,则称它们为强连通的
两个顶点是强连通的当且仅当它们都在一个普通的有向环中
强连通的性质(强连通是一种等价关系):
自反性:任意顶点到自己都是强连通的
对称性
传递性
强连通分量: 强连通将所有顶点分为了一些等价的部分,每个部分都由互相均为强连通的顶点的最大子集组成的。我们将这些子集称为强连通分量。例如下图含有5个强连通分量:
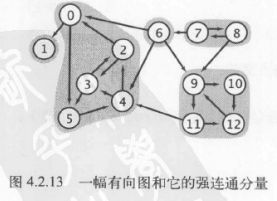
强连通分量是基于顶点的,不是基于边的,有些边的两个顶点可能在不同的强连通分量中
Kosaraju算法
代码很简单:按照 反向图顶点排序的 逆后序的顺序再做dfs就行了(虽然一次dfs只能证明s->v,但是由于采用反向图的逆后序,v->s已经天然证明了(而且这个v->s的证明还用了前面的s->v的结果!))
public class KosarajuSharirSCC {
private boolean[] marked; // marked[v] = has vertex v been visited?
private int[] id; // id[v] = id of strong component containing v
private int count; // number of strongly-connected components
public KosarajuSharirSCC(Digraph G) {
// compute reverse postorder of reverse graph
DepthFirstOrder dfs = new DepthFirstOrder(G.reverse());
// run DFS on G, using reverse postorder to guide calculation
marked = new boolean[G.V()];
id = new int[G.V()];
for (int v : dfs.reversePost()) {
if (!marked[v]) {
dfs(G, v);
count++;
}
}
// check that id[] gives strong components
assert check(G);
}
// DFS on graph G
private void dfs(Digraph G, int v) {
marked[v] = true;
id[v] = count;
for (int w : G.adj(v)) {
if (!marked[w]) dfs(G, w);
}
}
public int count() {
return count;
}
public boolean stronglyConnected(int v, int w) {
return id[v] == id[w];
}
public int id(int v) {
return id[v];
}
// does the id[] array contain the strongly connected components?
private boolean check(Digraph G) {
TransitiveClosure tc = new TransitiveClosure(G);
for (int v = 0; v < G.V(); v++) {
for (int w = 0; w < G.V(); w++) {
if (stronglyConnected(v, w) != (tc.reachable(v, w) && tc.reachable(w, v)))
return false;
}
}
return true;
}
}传递闭包
上面的check方法有一个传递闭包类,就是判断两点的是否连通(能否到达)
传递闭包就是另一种图(这个图(存图的二维矩阵中)的每个位置不是存直接相连的边,而是存 “两者是否相连”的一个布尔值,能连通就是true)


类中构造函数所需的空间和V^2成正比,时间和V(V+E)成正比
public class TransitiveClosure {
private DirectedDFS[] tc; // tc[v] = reachable from v
public TransitiveClosure(Digraph G) {
tc = new DirectedDFS[G.V()];
for (int v = 0; v < G.V(); v++)
tc[v] = new DirectedDFS(G, v);
}
public boolean reachable(int v, int w) {
return tc[v].marked(w);
}
}