ID3算法
ID3算法是J. Ross Quinlan在1975提出的分类预测算法,当时还没有数据挖掘吧,哈哈哈。该算法的核心是“信息熵”,属于数学问题,我也是从这里起发现数据挖掘最底层最根本的不再是编程了,而是数学,编程只是一种实现方式而已,数学才是基础,如:朴素贝叶斯分类,小波聚类,尤其是我正在搞的支持向量机,它就是高等代数,空间解析几何,概率统计的综合应用。记得读本科时,朱琛学姐说过,数学学得再好也不为过。我现在深刻体会到了。
信息熵就是一组数据包含的信息,概率的度量。一组数据越有序信息熵也就越低,极端时如果一组数据中只有一个非0,其它都是0,那么熵等于0,因为只有可能是这个非0的情况发生,它给人们的信息已经确定了,或者说不含有任何信息了,因为信息熵含量为0。一组数据越无序信息熵也就越高,极端时如果一组数据均匀分布,那么它的熵最大,因为我们不知道那种情况发生的概率大些。假如一组数据由{d1,d2,...,dn}构成,其和是sum,那么求信息熵的公式是![]() 。
。
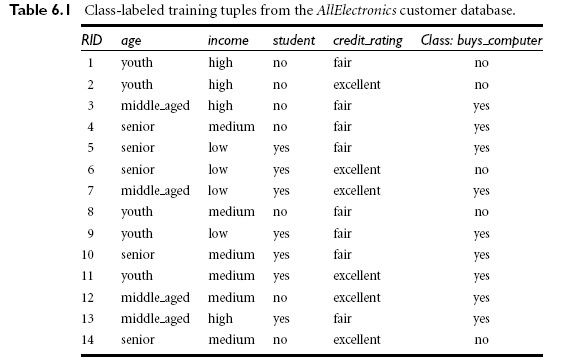
分类预测算法属于有指导学习,方法是通过训练数据,按照参考属性对目标属性的依赖程度对参考属性分级别处理,这种分级别处理体现在创建决策树,目的是通过生成的判别树,产生规则,用来判断以后的数据。以如下数据为例:
共14条记录,目标属性是,是否买电脑,共有两个情况,yes或者no。参考属性有4种情况,分别是,age,income,student,credit_rating。属性age有3种取值情况,分别是,youth,middle_aged,senior,属性income有3种取值情况,分别是,high,medium,low,属性student有2种取值情况,分别是,no,yes,属性credit_rating有2种取值情况,分别是fair,excellent。我们先求参考属性的信息熵:
![]() ,式中的5表示5个no,9表示9个yes,14是总的记录数。接下来我们求各个参考属性在取各自的值对应目标属性的信息熵,以属性age为例,有3种取值情况,分别是youth,middle_aged,senior,先考虑youth,youth共出现5次,3次no,2次yes,于是信息熵:
,式中的5表示5个no,9表示9个yes,14是总的记录数。接下来我们求各个参考属性在取各自的值对应目标属性的信息熵,以属性age为例,有3种取值情况,分别是youth,middle_aged,senior,先考虑youth,youth共出现5次,3次no,2次yes,于是信息熵:
类似得到middle_aged和senior的信息熵,分别是:0和0.971。整个属性age的信息熵应该是它们的加权平均值:
![]() 。下面引入信息增益(information gain)这个概念,用Gain(D)表示,该概念是指信息熵的有效减少量,该量越高,表明目标属性在该参考属性那失去的信息熵越多,那么该属性越应该在决策树的上层(如果不好理解,可以用极限的方法,即假如在age属性上,当为youth时全部是on,当为middle时也全部是no,当为senior时全不是yes,那么Hage(D)=0)。
。下面引入信息增益(information gain)这个概念,用Gain(D)表示,该概念是指信息熵的有效减少量,该量越高,表明目标属性在该参考属性那失去的信息熵越多,那么该属性越应该在决策树的上层(如果不好理解,可以用极限的方法,即假如在age属性上,当为youth时全部是on,当为middle时也全部是no,当为senior时全不是yes,那么Hage(D)=0)。![]() ,类似可以求出Gain(income)=0.029,Gain(stduent)=0.151,Gain(credit_rating)=0.048。最大值为Gain(age),所以首先按照参考属性age,将数据分为3类,如下:
,类似可以求出Gain(income)=0.029,Gain(stduent)=0.151,Gain(credit_rating)=0.048。最大值为Gain(age),所以首先按照参考属性age,将数据分为3类,如下: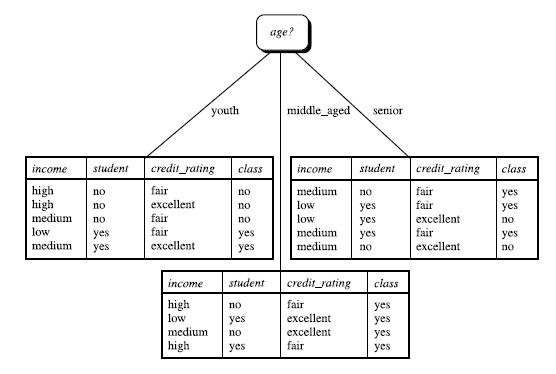
然后分别按照上面的方法递归的分类。递归终止的条件是,1,当分到某类时,目标属性全是一个值,如这里当年龄取middle_aged时,目标属性全是yes。2,当分到某类时,某个值的比例达到了给定的阈值,如这里当年龄取youth时,有60%的是no,当然实际的阈值远远大于60%。
ID3算法有很多变种,但是基本思想不变。但是它很可能需要多次遍历数据库,效率不高,不然朴素贝叶斯分类。