算法——字符串、序列问题

1、求一个字符串中连续出现次数最多的子串

《程序员面试宝典》 P237
字符串中连续出现次数最多的子串，例如字符串“abababc”,最多连续出现的为ab，连续出现三次。
【算法思路】
首先 获得后缀数组
例如：abcbcbcabc的后缀数组为：
abcbcbcabc
bcbcbcabc
cbcbcabc
bcbcabc
cbcabc
bcabc
cabc
abc
bc
c
然后
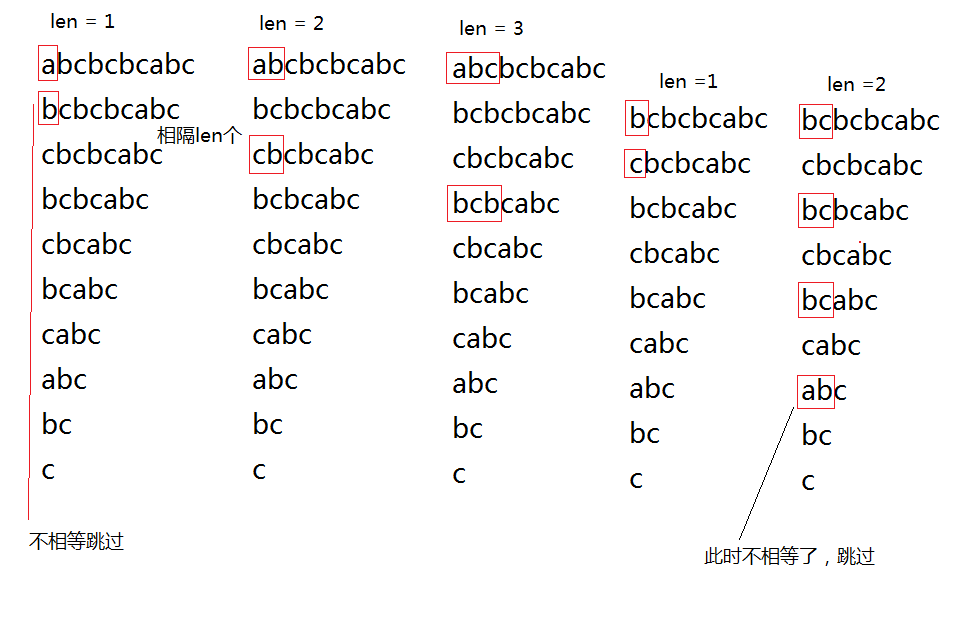
第一趟，比较后缀数组的第一个组数abcbcbcabc
1.第一行第一个字符a,与第二行第一个字符b比较，不等，则
2.第一行前两个字符ab，与第三行前两个字符cb比较，不等，则
3.第一行前三个字符abc,与第四行前三个字符bcb比较，不等，则
4.第一行前四个……
第二趟，比较后缀数组的第一个组数bcbcbcabc
…….

上述过程就相当于在原始字符串中，
第一趟，a与b比较，ab与cb比较，abc与bcb比较，abcb与cbca比较，abcbc与bcabc比较，abcbcb与cabc比较……
第二趟，b与c比较，bc与bc比较（相等，则继续向后取长度为2的子串比较，碰到不等为止，本例中因碰到ab停止），bcb与cbc比较……
第三趟，c与b比较，cb与cb比较（相等），cbc与bca比较……
……
使用后缀数组方便编程实现

自己实现的代码：

int getnum_substr(char *s, int n)
{
    int i,j,len,sum,max_cnt = 1;
    char max_s[30];

    for(i=0; i<n; ++i)  //第i趟的后缀数组
    {
        //每次从s[i]开始比较1~(n-i)/2的长度的子串
        //是否与后面相邻位置相同长度的字串相同
        for(len=1; len <= (n-i)/2; ++len)  //每次比较的长度增加1
        {
            sum = 1;
            j = i + len;   //j首先指向s[i+len]的位置
            while(j+len<=n && !strncmp(s+i,s+j,len))  //判断j所在的len长度的字串是否越界:j+len-1<=n-1
            {
                sum++;
                j += len;
            }
            if(sum > max_cnt)
            {
                max_cnt = sum;
                strncpy(max_s,s+i,len);
                max_s[len] = '\0';
            }
        }
    }

    printf("%s %d\n",max_s,max_cnt);
    return max_cnt;
}

2、求一个字符串中的最长重复子串

《程序员面试宝典》 P238
自己写的代码，
【思路】：

//求一个字符串中的最长重复子串
int get_maxrpt_substr(char *s)
{
    int i,j,len,n,max_len,tmp_len,index;
    char max_s[30];
    n = (int)strlen(s);

    max_len = 1;
    for(i=0; i<n; ++i)
    {        
        for(len=(n-i)/2; len>0; --len)
        {
            //寻找s[i]~s[i+len-1]这个字符串相等的字串
            for(j=i+len; j+len<=n && strncmp(s+i,s+j,len); ++j)  
            ;
            if(j+len<=n)  //找到没必要继续往下比较,因为len是递减的。
                break;
        }
        if(len > max_len)
        {
            strncpy(max_s,s+i,len);
            max_s[len] = '\0';
            printf("%s\n",max_s);
            max_len = len;
            index = i;
        }
    }

    printf("i:%d %d\n",index,max_len);
}

统计1到N中包含数字1的个数

《程序员面试宝典》 P240
例如f(13) = 6 (1,2,3,4,5,6,7,8,9,10,11,12,13)中1的个数为6(1,10,11,12,13)
其中n<=4 000 000 000

KMP 字符串匹配的KMP算法

【基本思想】
直到字符串有一个字符，与搜索词（字串）对应的字符不相同时，一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是”ABCDAB”。KMP算法的想法是，设法利用这个已知信息，不要把”搜索位置”移回已经比较过的位置，继续把它向后移，这样就提高了效率。


　　已知空格与D不匹配时，前面六个字符”ABCDAB”是匹配的。查表可知，最后一个匹配字符B对应的”部分匹配值”为2，因此按照下面的公式算出向后移动的位数：
　　移动位数 = 已匹配的字符数 - 对应的部分匹配值
　　因为 6 - 2 等于4，所以将搜索词向后移动4位。

http://kb.cnblogs.com/page/176818/
http://www.cnblogs.com/goagent/archive/2013/05/16/3068442.html
英文：http://jakeboxer.com/blog/2009/12/13/the-knuth-morris-pratt-algorithm-in-my-own-words/