编程验证带权图的最短路径路由算法

       在在一个带权图中，从某一个单源节点，走到其他节点，如何求得所有路径中的最短路径，是单元节点最短路径问题。而在路由算法中，与此类似，可以抽象出该模型来。迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Floyd算法，是另一个求最短路径的经典算法，不同于Dijikstra算法，是求带全图中每一对节点之间的最短路径。这两个算法所针对的带全图既可以是有向图，也可以是无向图。本文在迪杰斯特拉算法和Floyd算法的基础上，通过C语言程序，构建一个无向带权图，以程序的方式来验证最短路径路由算法。从而提供两种解决最短路径路由的思路。

1带全图相关知识介绍

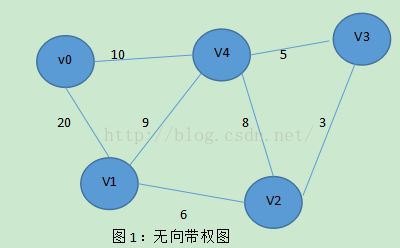
       图是数据结构中的一种数据组织方式，由节点和边构成，其中边既可以是有向边，也可以是无向边。图中的边为有向边的图叫有向图，图中边为无向边的图叫无向图。本文所探讨的两种最短路劲算法，既可以用于解决有向图，也可以用于解决无向图。如下图1所示，是一个含有五个节点的带权无向图。

       在该图中，拥有五个节点，七条边，每一条边上的数字代表该边的权重，它可以代表距离、耗费、时间或其他意义。在路由算法中，即可以代表两个路由节点之间的路径长度和耗费，因此通过路由算法，选择一条花费最短的路径，具有积极的作用。

2迪杰斯特拉算法原理简介

Dijikstra算法是典型的求单源节点到其他节点的最短路径算法。[12]其基本思想是，通过构建一个节点之间的邻接矩阵来表示节点之间的路径长度。假设我们需要求得是节点v到其他节点的最短路径，在最开始初始化v到其他节点的距离，当v与其他节点之间存在路径的时候，即将该节点之间的路径长度赋为该路径长度的权值，如果v到某个节点之间不存在直接路径，则将v到该节点的权值赋为无穷大（在程序中使用一个较大的数值来代表无穷大）。

如上图1对应的邻接矩阵为：

  v0  v1  v2  v3  v4

V0  0  20  ∞  ∞ 10 

V1  20  0  6  ∞  9

V2  ∞  6       0          3          8   

V3  ∞   ∞ 3          0        5

V4  10  9  8   5  0 

   算法的基本思想是按照路径长度的增长来通过迭代，依次求得v0节点到其他节点的路径长度，当经过n次迭代后，即可求出v0到其他n-1个节点之间的最短路径长度。首先将节点分为两个集合S1和S2，其中S1初始只包含v0节点，S2初始为其他节点，然后算法按照以下规则来迭代：

（1）从集合S2中选择一个节点vi使其到v0节点之间的距离最短，并把vi加入到S1集合中；

（2）用vi作为中间节点来过渡，判断是否能通过vi节点作为中间节点，使得从v0到S2集合中其他的节点路径更短，如果通过vi作为中间节点的过渡得到的距离更短，即更新v0到S2中节点之间的距离权值；

（3）重复（1）~（2）的迭代过程，知道S2集合中不再有节点为止。

   单源点最短路径问题是给定带权有向图 G 和源点 v, 求从v 到 G 中其余各顶点的最短路径。Dijkstra 提出了一个按最短路径递增的次序产生最短路径的算法，其时间开销为 2n(n- 1)+n(n 为图 G 的顶点个数)。如果求所有点对间的最短路径，解决这个问题的一个方法是: 每次以一个顶点为源点，重复执行Dijkstra 算法n次，这样便可求得每一对顶点间的最短路径。总的执行时间为 O(n^3) 。Floyd 提出了解决每一对顶点间最短路径的一个方法， 该方法形式上更简洁些，但其总的执行时间为O(n^3) 。这两种方案的缺陷是时间开销为点数n的多项式, 不能根据图的边数、边的实际分布和点数联合动态调整算法本身的时间开销,,以使得算法的运行时间极小化，运算速度极大化。

3 Floyd算法原理简介

   Floyd算法又称为插点法，是一种用于寻找给定的加权图中多源点之间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

   通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。采用松弛技术（松弛操作），对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3)。

   其核心思想是，通过三重嵌套循环，每次选取一个节点去作为中间过渡节点，判断其他任意两对节点间，如果通过所选取的节点来过渡，得到的路径长度较短，则更新该对节点之间的路径距离，即更新所对应的的距离矩阵的数值，这样最外层循环控制的是所选取的节点作为更新节点，内部嵌套的两个循环是作为遍历选取任意两个节点，来判断是否通过所选取的中间节点来过渡得到的距离更短，这样最外层循环，每一次进行下一步，距离举证将会得到更新，即Warshall方法中所对应的的矩阵更新变化。

   优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。

   缺点：时间复杂度比较高，不适合计算大量数据。

4 C语言程序验证最短路径路由算法

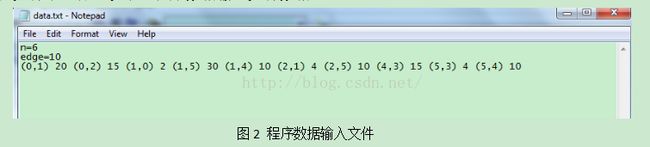
  在程序中采用C语言程序来验证最短路径算法，分别验证了单源节点到其它节点的最短路径迪杰斯特拉算法和每对节点间的最短路径Floyd算法。在该程序中将数据的输入和输出放在文件中进行。以下是程序数据输入文件数据：

  程序数据输入文件用来描述构建的无向带权图，如n=6代表有6个节点，edge=10代表图中有10条边，下面十对（）中间的数据分别描述了路径的起始节点后终端节点，括号后面的数字代表该条路径的权值。程序中设计到的几个主要函数、参数的交代（该部分在程序源代码中也通过注释的形式标明）：

#define ok 0 ：定义函数的返回值

#define eror 1 ：定义函数的返回值

#define maxOfInt 99999  ：定义最大的路径长度

int read_data(int ***a,int *n); ：从文件中读数据的函数

int ShortestPath_Floyd(int n,int ***p,int **D); ：Floyd算法函数

int ShortestPat_dijkstra(int *D,int **DG,int v0,int **p,int vexnum)： Dijkstra算法函数;

int draw_path(FILE **fp,int **p,int v0,int len);  //after each time call functions of dijkstra,get the path from p matrix.  ：生成最短路径上的节点顺序的函数。

5 程序运行结果

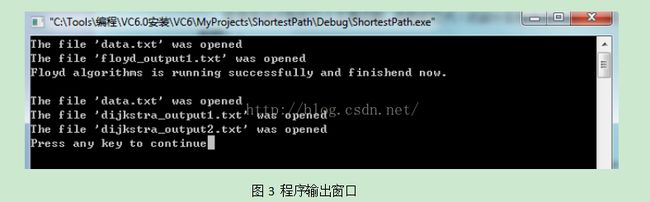
程序输出窗口只会输出提示程序是否运行正常的相关信息，而程序的结果将分别输出到三个txt文本中。下面分别展示：

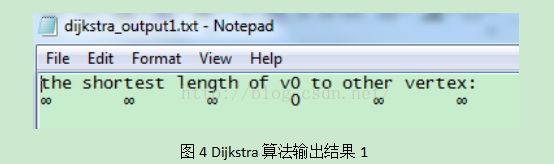
图4展示的是，最初从v0节点到其它节点的路径长度，从图中可以看出有很多节点在最初是不可达的，这将与下面的第二个输出结果图对比。

在该图中，分别找到了从v0节点到其它节点之间的路径是怎样的。此处只是部分输出图，在该程序中，运行验证了从其它节点出发的，最短路径。

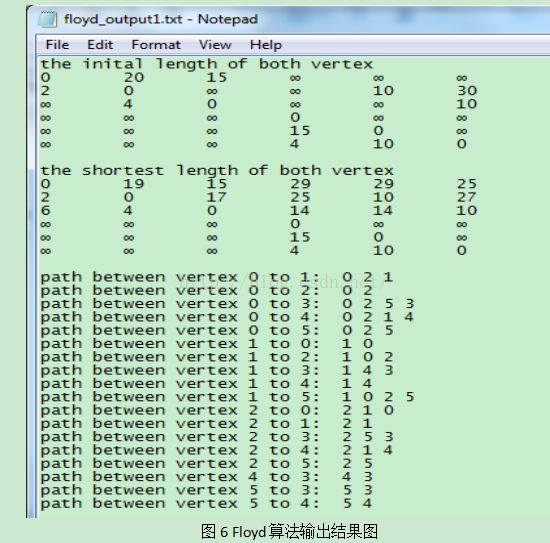
在图6中展示了调用Floyd算前和调用之后的最短路径矩阵的变化，明显第二个矩阵相比第一个矩阵，为无穷远的元素要少，而且相对应位置的值也要小。

6 程序源代码

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#define ok 0

#define eror 1

#define maxOfInt 99999

int read_data(int ***a,int *n);

int ShortestPath_Floyd(int n,int ***p,int **D);

int ShortestPat_dijkstra(int *D,int **DG,int v0,int **p,int vexnum);

int draw_path(FILE **fp,int **p,int v0,int len);  //after each time call functions of dijkstra,get the path from p matrix.

 

int main()

{

FILE *fpf=NULL,*fp=NULL;

int **D,n,***p,i,j,k,tempj,flag=0,* path,path_len, **pd,* mind;

//****Floyd algorithms area*****

read_data(&D,&n);

if( (fpf  = fopen( "floyd_output1.txt", "w" )) == NULL )

{

printf( "The file 'floyd_output1.txt' was not opened\n" );

return eror;

}

else

printf( "The file 'floyd_output1.txt' was opened\n" );

p=(int ***)malloc(n*sizeof(int **));

path=(int *)malloc(n*sizeof(int));

for(i=0;i<n;++i)

{

p[i]=(int **)malloc(n*sizeof(int *));

for(j=0;j<n;++j)

p[i][j]=(int *)malloc(n*sizeof(int));

}

fprintf(fpf,"the inital length of both vertex\n");

for(i=0;i<n;++i)

{

for(j=0;j<n;++j)

{

if(D[i][j]==maxOfInt)

{

fprintf(fpf,"∞\t");

}

else

{

fprintf(fpf,"%d\t",D[i][j]);

}

}

fprintf(fpf,"\n");

}

ShortestPath_Floyd(n,p,D);

fprintf(fpf,"\nthe shortest length of both vertex\n");

for(i=0;i<n;++i)

{

for(j=0;j<n;++j)

{

if(D[i][j]==maxOfInt)

{

fprintf(fpf,"∞\t");

}

else

{

fprintf(fpf,"%d\t",D[i][j]);

}

}

fprintf(fpf,"\n");

}

//if there is a path between two vertex，then get it and write it to file.

for(i=0; i<n; ++i)

for(j=0; j<n; ++j)

{

if(i!=j&&D[i][j]<maxOfInt)

{

tempj=j;

path_len=0; 

do 

{

p[i][j][j]=0;

for(k=0; k<n; ++k)

{

if(k!=j&&memcmp(p[i][j],p[i][k],n*sizeof(int))==0)

{

path[path_len++]=k;

p[i][j][j]=1;

j=k;

break;

}

}

}while(k!=i);

j=tempj;

fprintf(fpf,"\npath between vertex %d to %d:  ",i,j);

for(k=path_len-1; k>=0; --k)

{

fprintf(fpf,"%d ",path[k]);

}

fprintf(fpf,"%d",j);

}

}

fprintf(fpf,"\n");

//******code area to free memory******

for(i=0;i<n;++i)

free(D[i]);

free(D);

for(i=0;i<n;++i)

{

for(j=0;j<n;++j)

free(p[i][j]);

free(p[i]);

}

free(p);

free(path);

if( fclose( fpf ) )

{

printf( "The file 'data.txt' was not closed\n" );

return eror;

}

printf("Floyd algorithms is running successfully and finishend now.\n");

 

//******dijkstra algorithms area*******

printf("\n");

read_data(&D,&n);

if( (fpf  = fopen( "dijkstra_output1.txt", "w" )) == NULL )

{

printf( "The file 'dijkstra_output1.txt' was not opened\n" );

return eror;

}

else

printf( "The file 'dijkstra_output1.txt' was opened\n" );

if( (fp  = fopen( "dijkstra_output2.txt", "w" )) == NULL )

{

printf( "The file 'dijkstra_output2.txt' was not opened\n" );

return eror;

}

else

printf( "The file 'dijkstra_output2.txt' was opened\n" );

mind=(int *)malloc(sizeof(int)*n);

pd=(int **)malloc(n*sizeof(int *));

for(i=0;i<n;i++)

pd[i]=(int *)malloc(n*sizeof(int));

ShortestPat_dijkstra(mind,D,3,pd,n);

fprintf(fpf,"the shortest length of v0 to other vertex:\n");

fprintf(fp,"the shortest length of both vertex:\n");

for(i=0;i<n;i++)

if(mind[i]<maxOfInt)

{

fprintf(fpf,"%d\t",mind[i]);

fprintf(fp,"%d\t",mind[i]);

}

else

{

fprintf(fpf,"∞\t");

fprintf(fp,"∞\t");

}

fprintf(fp,"\n");

draw_path(&fp,pd,0,n);

if( fclose( fpf ) )

printf( "The file 'dijkstra_output1.txt' was not closed\n" );

for(i=1;i<n;i++)

{

ShortestPat_dijkstra(mind,D,i,pd,n);

for(j=0;j<n;j++)

if(mind[j]<maxOfInt)

{

fprintf(fp,"%d\t",mind[j]);

}

else

{

fprintf(fp,"∞\t");

}

fprintf(fp,"\n");

draw_path(&fp,pd,i,n);

}

if( fclose( fp ) )

printf( "The file 'dijkstra_output2.txt' was not closed\n" );

//code area to free memory

for(i=0;i<n;++i)

{

free(D[i]);

free(pd[i]);

}

free(D);

free(pd);

return ok;

}

 

int ShortestPath_Floyd(int n,int ***p,int **D)

{

int v,w,u,i;

for(v=0; v<n; ++v)

for(w=0; w<n; ++w)

for(u=0; u<n; ++u)

{

p[v][w][u]=0;

if(D[v][w]<maxOfInt)

{

p[v][w][v]=1;

p[v][w][w]=1;

}

}

for(u=0; u<n; ++u)

for(v=0; v<n; ++v)

for(w=0; w<n; ++w)

{

if(D[v][u]+D[u][w]<D[v][w])

{

D[v][w] = D[v][u] + D[u][w];

for(i=0; i<n; ++i)

{

if(p[v][u][i]==1||p[u][w][i]==1)

p[v][w][i]=1;

else

p[v][w][i]=0;

}

}

}

return ok;

}

// D用来存储v0到其他节点距离，DG为邻接矩阵，p用来存储路径上的点信息，vexnum是点的个数

int ShortestPat_dijkstra(int *D,int **DG,int v0,int **p,int vexnum) 

{ 

int v,w,i,min,* final;

final=(int *)malloc(vexnum*sizeof(int));

for(v=0;v<vexnum;++v)

{

final[v]=0;

D[v]=DG[v0][v];

for(w=0;w<vexnum;++w)

p[v][w]=0;

if(D[v]<maxOfInt)

{

p[v][v0]=1;

p[v][v]=1;

}

}

final[v0]=1;

for(i=1;i<vexnum;i++)

{

min=maxOfInt;

v=-1;

for(w=0;w<vexnum;++w)

if(!final[w])

if(D[w]<min)

{

v=w;

min=D[w];

}

if(v==-1)   //此种情况代表所给节点到其他节点不可达。

return eror;

final[v]=1;

for(w=0;w<vexnum;w++)

if(!final[w]&&(min+DG[v][w]<D[w]))

{

D[w]=min+DG[v][w];

memcpy(p[w],p[v],sizeof(int)*vexnum);

p[w][w]=1;

}

}

return ok;

}

int draw_path(FILE **fp,int **p,int v0,int len)

{

int i,temp,*path,j,k=0;

path=(int *)malloc(len*sizeof(int));

for(i=0;i<len;++i,k=0)

{

temp=i;

if(i!=v0)

{

do

{

p[i][i]=0;

for(j=0;j<len;++j)

{

if(i!=j&&memcmp(p[i],p[j],sizeof(int)*len)==0)

{

path[k++]=j;

p[i][i]=1;

i=j;

break;

}

}

}while(i!=v0&&j<len);

}

if(temp!=v0&&k>0)

{

fprintf(*fp,"\npath between vertex %d to %d:  ",v0,temp);

for(j=k-1;j>=0;--j)

fprintf(*fp,"%d ",path[j]);

fprintf(*fp,"%d ",temp);

fprintf(*fp,"\n");

}

i=temp;

}

free(path);

return ok;

}

 

int read_data(int ***a,int *n)

{

FILE * fp;

int i=0,x=0,y=0,edge=0;

if( (fp  = fopen( "data.txt", "r" )) == NULL )

{

printf( "The file 'data.txt' was not opened\n" );

return eror;

}

else

{

printf( "The file 'data.txt' was opened\n" );

fscanf(fp,"n=%d\n",&(*n));

fscanf(fp,"edge=%d\n",&edge);

(*a)=(int **)malloc((*n)*sizeof(int*));

for(i=0;i<*n;++i)

(*a)[i]=(int*)malloc((*n)*sizeof(int));

for(x=0; x<*n; ++x)

for(y=0; y<*n; ++y)

{

if(x!=y)

(*a)[x][y]=maxOfInt;

else

(*a)[x][y]=0;

}

for(i=0;i<edge;i++)

{

fscanf(fp,"(%d,%d) ",&x,&y);

fscanf(fp,"%d ",&(*a)[x][y]);

}

if( fclose( fp ) )

printf( "The file 'data.txt' was not closed\n" );

return ok;

}

}