Logistic Regression详解

Logistic Regression（简称LR）作为一个经典的机器学习分类算法，由于其出众的分类效果和简单的模型，在学术界和工业界都占有重要的地位。此外，Logistic Regression构造目标函数的思路也很值得学习和借鉴。

一、二分类问题：

Logistic函数：

      Logistic Regression的核心是Logistic函数，损失函数的构造也正是利用了Logistic函数的特点。Logistic函数形式如下：

δ(a)=11+e−a

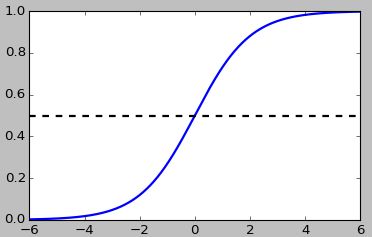
从图中可以发现，当 a 接近6时，函数值接近于1；当 a 接近-6时，函数值接近于0。这为0-1分类提供了很好的特性。

损失函数：

Logistic Regression用“Logistic函数+线性模型”来预测0-1类别的概率：

P(C1|x)=δ(xw)=11+e−xw

其中 x1×d 是输入样本， wd×1 是投影向量。当 xw 的值较大时， P(C1|x) 接近于1。

P(C0|x)=1−P(C1|x)

定义样本的标签为 ti∈{0,1} ，则训练数据集上的似然函数为：

P(t|w)=∏i=1nP(C1|xi)ti(1−P(C1|xi))1−ti=∏i=1nP(C1|xi)tiP(C0|xi)1−ti

很巧妙的，当 ti=1 时（类别1）， P(t|w) 增加一项 P(C1|xi) ；当 ti=0 时（类别0）， P(t|w) 增加一项 P(C0|xi) 。这个小技巧已经被广泛应用，不得不佩服研究人员的智慧。

构造损失函数（Negative Log-Likelihood）：也称为交叉熵（cross-entropy）误差函数，对 P(t|w) 取负对数

E(w)=−lnP(t|w)=−∑i=1n{tilnP(C1|xi)+(1−ti)ln(1−P(C1|xi))}

对损失函数进行拆分：

Cost={−lnP(C1|xi)−ln(1−P(C1|xi))ifti=1,ifti=0.

       

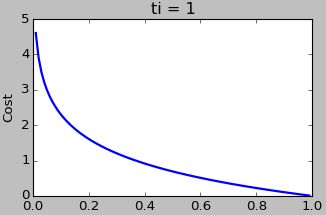
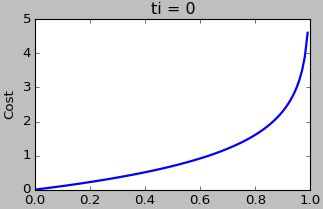
两幅Cost图很直观的展示了 P(C1|xi) 和 ti 的值对Cost的影响。当 ti=1 时， P(C1|xi) 的值越大，Cost越小； ti=0 时相反。

求偏导：

最小化损失函数求 w ，通常可以使用梯度下降算法得到 w 的局部最优值。对梯度下降算法的介绍可以参考我的另一篇博文： 深入了解梯度下降算法

∂P(C1|x)∂w=∂11+e−xw∂w=∂(1+e−xw)−1∂w=−e−xw⋅(−x⊤)(1+e−xw)2=e−xw1+e−xw⋅11+e−xw⋅x⊤=(1−P(C1|x))P(C1|x)x⊤

损失函数对 w 求偏导:

∂E(w)∂w=−∑i=1n{tiP(C1|xi)∂P(C1|xi)∂w+1−ti1−P(C1|xi)(−∂P(C1|xi)∂w)}=−∑i=1n{ti(1−P(C1|xi))x⊤i−(1−ti)P(C1|xi)x⊤i}=−∑i=1n{ti−tiP(C1|xi)−P(C1|xi)+tiP(C1|xi)}x⊤i=∑i=1n{P(C1|xi)−ti}x⊤i

至此，已经可以很容易写出二分类问题Logistic Regression分类器的代码了，在此不再赘述。

二、多类情况：

   多分类问题的Logistic Regression与二分类问题很相似，多分类Logistic Regression用的是Softmax函数，但是在本质上Softmax函数和Logistic函数优化目标是一致的。

Softmax：

P(Y=i|x~,W~,b)=softmaxi(x~W~+b)=ex~W~i+bi∑jex~W~j+bj

   在实际中，常把偏置 b 加入到 W~ 矩阵内： Wi=[W~i,bi] 。同时在样本 x~ 的最后扩展一维： x=[x~,1] 。Softmax式子简化后的形式是：

P(Y=i|x,W)=softmaxi(xW)=exWi∑jexWj

类别预测：

ypred=maxiP(Y=i|x,W)

符号定义说明：

• 向量 x1×d 是输入数据，整个训练集为 Xn×d ，每一行是一个样本；
• 矩阵 Wd×K 是投影矩阵,每一列对应于一个类别，共有K个类；
• 数据的原始标签为 yn×1 ，对应于 n 个样本。

损失函数：

   把原始标签信息写成矩阵的形式 Tn×K ，如果第i个样本属于类别k，则 tik=1 ，否则 tik=0 :

tik={10iflabel(xi)=k,iflabel(xi)≠k.

每个样本只属于一个类，所以可以得到（这个式子会在后面求偏导的时候用到）：

∑ktik=1

似然函数：

P(T|W)=∏i=1nP(Y=yi|Xi,W)=∏i=1n∏k=1KP(Y=k|Xi,W)tik

构造损失函数（Negative Log-Likelihood）：

E(W)=−lnP(T|W)=−∑i=1n∑k=1KtiklnP(Y=k|Xi,W)

这是多分类问题的交叉熵（cross-entropy）误差函数。

求偏导：

为了符号的简洁，记 Pik=P(Y=k|Xi,W)=eXiWk∑jeXiWj

∂Pic∂Wc=eXiWc∑jeXiWjX⊤i−(eXiWc)2(∑jeXiWj)2X⊤i=(Pic−P2ic)⋅X⊤i

∂Pik∂Wc=−eXiWk⋅eXiWc(∑jeXiWj)2X⊤i=−PikPic⋅X⊤i,k≠c

损失函数对 Wc 求偏导：

∂E(W)∂Wc=−(∂∑ni=1ticlnPic∂Wc+∂∑ni=1∑k≠ctiklnPik∂Wc)=−(∑i=1ntic1Pic⋅(Pic−P2ic)⋅X⊤i+∑i=1n∑k≠ctik1Pik(−PikPic)⋅X⊤i)=−(∑i=1ntic(1−Pic)−∑i=1n∑k≠ctikPic)⋅X⊤i=−(∑i=1ntic−∑i=1n∑k=1KtikPic)⋅X⊤i,已知∑k=1Ktik=1=−(∑i=1ntic−∑i=1nPic)⋅X⊤i=∑i=1n(Pic−tic)⋅X⊤i

有了偏导之后，就可以用梯度下降算法优化参数 W 。也可以用BFGS或L-BFGS等算法进行优化。

和二分类问题的比较：

1、在构造损失函数时，多分类问题和二分类问题都是用的负对数似然作为目标函数。

2、优化方法相同，都可以用梯度下降算法寻找局部最优值。并且两种情况下偏导的结果也是惊人的一致，主要还是由于Softmax和Logistic函数本质上是一致的。

3、Softmax函数：

P(Y=i|x,W)=softmaxi(xW)=exWi∑jexWj=exWi∑j≠iexWj+exWi=1∑j≠iexWjexWi+1=1(∑j≠iexWj)e−xWi+1

当 ∑j≠iexWj=1 时

softmaxi(xW)=11exWi+1=1e−xWi+1

所以Softmax和Logistic函数主要的区别就在于Logistic函数固定为常数1，而Softmax是一个实数 ∑j≠iexWj ，并且是在迭代过程中不断更新的。

三、参考资料：

[1] M.Bishop: Pattern Recognition and Machine Learning(PRML，机器学习圣经)

[2]Andrew Ng: Stanford Machine Learning(Coursera)