hihoCoder[Offer收割]编程练习赛1题目解析
题目1 : 九宫
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。
三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:“二四为肩,六八为足,左三右七,戴九履一,五居其中”,通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Ho编写了一个处理数据包的程序。程序的输入是一个包含N个数据包的序列。每个数据包根据其重要程度不同,具有不同的"延迟惩罚值"。序列中的第i个数据包的"延迟惩罚值"是Pi。如果N个数据包按照<Pi1, Pi2, ... PiN>的顺序被处理,那么总延迟惩罚SP=1*Pi1+2*Pi2+3*Pi3+...+N*PiN(其中i1, i2, ... iN是1, 2, 3, ... N的一个排列)。
小Ho的程序会依次处理每一个数据包,这时N个数据包的总延迟惩罚值SP为1*P1+2*P2+3*P3+...+i*Pi+...+N*PN。
小Hi希望可以降低总延迟惩罚值。他的做法是在小Ho的程序中增加一个大小为K的缓冲区。N个数据包在被处理前会依次进入缓冲区。当缓冲区满的时候会将当前缓冲区内"延迟惩罚值"最大的数据包移出缓冲区并进行处理。直到没有新的数据包进入缓冲区时,缓冲区内剩余的数据包会按照"延迟惩罚值"从大到小的顺序被依次移出并进行处理。
例如,当数据包的"延迟惩罚值"依次是<5, 3, 1, 2, 4>,缓冲区大小K=2时,数据包被处理的顺序是:<5, 3, 2, 4, 1>。这时SP=1*5+2*3+3*2+4*4+5*1=38。
现在给定输入的数据包序列,以及一个总延迟惩罚阈值Q。小Hi想知道如果要SP<=Q,缓冲区的大小最小是多少?
输入
Line 1: N Q
Line 2: P1 P2 ... PN
对于50%的数据: 1 <= N <= 1000。
对于100%的数据: 1 <= N <= 100000, 0 <= Pi <= 1000, 1 <= Q <= 1013。
输出
输出最小的正整数K值能满足SP<=Q。如果没有符合条件的K,输出-1。
样例输入
5 38
5 3 1 2 4
样例输出
2
用优先队列模拟缓冲区的功能,二分搜索得到最小的缓冲区。
AC代码:
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
在遥远的未来,小Hi成为了地球联邦外空间联合开发工作组的一员,前往一颗新发现的星球开发当地的重金属资源。
为了能够在当地生存下来,小Hi首先要建立一个基地。建立基地的材料可以直接使用当地的石材和富裕的重金属资源。基地建设分为N级,每一级都需要达成K的建设值后才能够完成建设,当前级别的建设值溢出后不会影响到下一级的建设。
小Hi可以产出的重金属资源按照精炼程度分为M级,根据开采的数量和精炼的工艺,可以将获取精炼程度为第i级的重金属资源的成本量化为Ai。
在建设第1级基地时,一块精炼度为i的重金属可以提供Bi的建设值,此后基地的级别每提高一级,建设值将除以T并下取整(整除)。
现给定N、M、K、T、A[]和B[],小Hi需要你帮助他计算他完成基地建设的最小成本。
输入
输入包含多组测试数据。
输入的第一行为一个整数Q,表示测试数据的组数。
每组测试数据的第一行为4个整数N、M、K和T,意义如前文所述。
接下来的一行为M个整数,分别表示A1~AM。
接下来的一行为M个整数,分别表示B1~BM。
对于100%的数据,满足1<=N<=10,1<=M<=100,1<=K,T<=104。
对于100%的数据,满足Ai和Bi均为32位整型范围内的正整数。
对于100%的数据,满足1<=Q<=10。
输出
对于每组测试数据,如果小Hi最终能够完成基地建设,则输出小Hi完成基地建设所需要的最小成本,否则输出“No Answer”。
样例输入
2
2 2 2 2
1 3
1 2
2 2 2 2
1 2
1 1
样例输出
8
No Answer
题意有点绕,想清楚是完全背包问题以后还是比较简单的。
AC代码:
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi最近在玩一款组建舰队出海进行战争的游戏,在这个游戏中,小Hi需要根据需要组建一只舰队,一支舰队里最多同时存在N艘舰船,每艘舰船最多同时装备M个装备。
在一次关卡中,小Hi希望能够组建一只仅由航母构成的舰队,这意味着所有舰船的装备都是某种类型的飞机,小Hi将要使用的飞机有两种类型:对空飞机和对舰飞机,顾名思义,对空飞机用于和敌对舰船搭载的飞机进行对抗,而对舰飞机则直接用于攻击敌对舰船本身。
每艘航母的M个装备栏位是不一样的,我们可以用“搭载量”来对其进行量化描述,有些装备栏位的搭载量较高,有些装备栏位的搭载量较低,对于第i艘舰船,我们用Ai,j表示其第j个装备栏位的搭载量。
小Hi的军备库里有T架飞机,我们Bi表示第i架飞机的对空攻击力,并用Ci表示第i架飞机的对舰攻击力,其中对空飞机的对舰攻击力为0,对舰飞机的对空攻击力为0。
为舰船装备飞机,会提高舰队的“制空值”和“伤害值”。舰队的制空值为所有飞机的对空攻击力与其对应的装备栏位的搭载量的乘积之和,即:
制空值=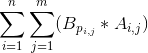
其中pi,j表示放置在第i艘舰船的第j个装备栏位的飞机编号。同理,舰队的伤害值为所有飞机的对舰攻击力与其对应的装备栏位的搭载量的乘积之和,即
伤害值=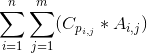
为了能够顺利的通过关卡,小Hi需要使得舰队的制空值不低于一个给定的值S,并且希望在这个条件下舰队的伤害值越高越好,这样能够尽量减少舰队的损耗。
同时,由于一艘舰船至少要装备一架对舰飞机才能够在炮击战中发动攻击,所以小Hi也好奇是否存在在满足制空值限制且伤害值最高的情况下,同时满足每一艘舰船至少装备一架对舰飞机。
而这个问题,就有待你来进行计算了~
输入
输入第一行为一个正整数Q,表示测试数据的组数。
在每组测试数据的第一行,为4个正整数N、M、T和S,意义如之前所述。
第2行~第n+1行,每行m个正整数,对应矩阵A。
第n+2行,为T个正整数B1 .. BT。
第n+3行,为T个正整数C1 .. CT。
对于30%的数据,满足N<=2,M<=2,T<=20,Q<=100。
对于剩下70%的数据,满足N<=4,M<=4,T<=1000,Q<=3。
对于100%的数据,满足1<=Ai,j, Bi, Ci <= 1000,0<= S <= 108。
输出
对于每组测试数据,如果存在满足制空值限制的方案的话,则首先在第一行输出在满足制空值限制下能够达到的最大攻击力D,在第二行中,如果在满足制空值限制且伤害值最高的情况下,能够同时满足每一艘舰船至少装备一架对舰飞机,则输出Yes,否则输出No。
如果不存在满足制空值限制的方案的话,则输出一行Not Exist。
样例输入
3
1 2 1 38
4 5
0
5
1 2 8 7
1 4
0 3 2 0 0 2 0 0
5 0 0 3 3 0 3 4
2 1 4 29
5
3
0 4 3 0
1 0 0 3
样例输出
Not Exist
5
Yes
0
No
对值直接从小到大排序,然后就是枚举状态贪心计算。
AC代码:
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。
三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:“二四为肩,六八为足,左三右七,戴九履一,五居其中”,通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
有意思的是,所有的三阶幻方,都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小Hi准备将一个三阶幻方(不一定是上图中的那个)中的一些数组抹掉,交给邻居家的小朋友来进行还原,并且希望她能够判断出究竟是不是只有一组解。
而你呢,也被小Hi交付了同样的任务,但是不同的是,你需要写一个程序~
输入
输入仅包含单组测试数据。
每组测试数据为一个3*3的矩阵,其中为0的部分表示被小Hi抹去的部分。
对于100%的数据,满足给出的矩阵至少能还原出一组可行的三阶幻方。
输出
如果仅能还原出一组可行的三阶幻方,则将其输出,否则输出“Too Many”(不包含引号)。
样例输入
0 7 2
0 5 0
0 3 0
样例输出
6 7 2
1 5 9
8 3 4
比较简单的DFS。
AC代码:
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int MAXN=10;
int graph[MAXN],vis[MAXN],ans[MAXN];
int flag=0;
bool isok()
{
for(int i=1;i<=7;i+=3)
{
if((graph[i]+graph[i+1]+graph[i+2])!=15) return false;
}
for(int i=1;i<=3;i++)
{
if((graph[i]+graph[i+3]+graph[i+6])!=15) return false;
}
if((graph[1]+graph[5]+graph[9])!=15||(graph[3]+graph[5]+graph[7])!=15) return false;
return true;
}
void dfs(int pos)
{
if(pos==10&&isok())
{
flag++;
if(flag==1)
{
memcpy(ans,graph,sizeof(graph));
return;
}
}
if(graph[pos]) dfs(pos+1);
else
{
for(int i=1;i<=9;i++)
{
if(vis[i]) continue;
vis[i]=1;
graph[pos]=i;
dfs(pos+1);
vis[i]=0;
graph[pos]=0;
}
}
}
int main()
{
memset(vis,0,sizeof(vis));
for(int i=1;i<=9;i++)
{
scanf("%d",&graph[i]);
vis[graph[i]]=1;
}
dfs(1);
if(flag==1)
{
for(int i=1;i<=9;i++)
{
printf("%d%c",ans[i],(i%3==0)?'\n':' ');
}
}
else printf("Too Many\n");
} 题目2 : 优化延迟
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Ho编写了一个处理数据包的程序。程序的输入是一个包含N个数据包的序列。每个数据包根据其重要程度不同,具有不同的"延迟惩罚值"。序列中的第i个数据包的"延迟惩罚值"是Pi。如果N个数据包按照<Pi1, Pi2, ... PiN>的顺序被处理,那么总延迟惩罚SP=1*Pi1+2*Pi2+3*Pi3+...+N*PiN(其中i1, i2, ... iN是1, 2, 3, ... N的一个排列)。
小Ho的程序会依次处理每一个数据包,这时N个数据包的总延迟惩罚值SP为1*P1+2*P2+3*P3+...+i*Pi+...+N*PN。
小Hi希望可以降低总延迟惩罚值。他的做法是在小Ho的程序中增加一个大小为K的缓冲区。N个数据包在被处理前会依次进入缓冲区。当缓冲区满的时候会将当前缓冲区内"延迟惩罚值"最大的数据包移出缓冲区并进行处理。直到没有新的数据包进入缓冲区时,缓冲区内剩余的数据包会按照"延迟惩罚值"从大到小的顺序被依次移出并进行处理。
例如,当数据包的"延迟惩罚值"依次是<5, 3, 1, 2, 4>,缓冲区大小K=2时,数据包被处理的顺序是:<5, 3, 2, 4, 1>。这时SP=1*5+2*3+3*2+4*4+5*1=38。
现在给定输入的数据包序列,以及一个总延迟惩罚阈值Q。小Hi想知道如果要SP<=Q,缓冲区的大小最小是多少?
输入
Line 1: N Q
Line 2: P1 P2 ... PN
对于50%的数据: 1 <= N <= 1000。
对于100%的数据: 1 <= N <= 100000, 0 <= Pi <= 1000, 1 <= Q <= 1013。
输出
输出最小的正整数K值能满足SP<=Q。如果没有符合条件的K,输出-1。
样例输入
5 38
5 3 1 2 4
样例输出
2
用优先队列模拟缓冲区的功能,二分搜索得到最小的缓冲区。
AC代码:
#include<cstdio>
#include<queue>
using namespace std;
const int MAXN=100005;
int P[MAXN],N;
long long Q;
bool isOk(int value)
{
long long cnt=0;
int index=1;
priority_queue<int> queue;
for(int i=1;i<=N;i++)
{
if(queue.size()==value)
{
int temp=queue.top();
queue.pop();
cnt+=temp*index++;
}
queue.push(P[i]);
}
while(queue.size())
{
int temp=queue.top();
queue.pop();
cnt+=temp*index++;
}
if(cnt<=Q) return true;
else return false;
}
int main()
{
while(scanf("%d%lld",&N,&Q)>0)
{
for(int i=1;i<=N;i++) scanf("%d",&P[i]);
int minn=1;int maxn=100000;
while(minn<=maxn)
{
int mid=(minn+maxn)/2;
if(isOk(mid)) maxn=mid-1;
else minn=mid+1;
}
if(minn>100000) minn=-1;
printf("%d\n",minn);
}
return 0;
}
题目3 : 建造基地
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
在遥远的未来,小Hi成为了地球联邦外空间联合开发工作组的一员,前往一颗新发现的星球开发当地的重金属资源。
为了能够在当地生存下来,小Hi首先要建立一个基地。建立基地的材料可以直接使用当地的石材和富裕的重金属资源。基地建设分为N级,每一级都需要达成K的建设值后才能够完成建设,当前级别的建设值溢出后不会影响到下一级的建设。
小Hi可以产出的重金属资源按照精炼程度分为M级,根据开采的数量和精炼的工艺,可以将获取精炼程度为第i级的重金属资源的成本量化为Ai。
在建设第1级基地时,一块精炼度为i的重金属可以提供Bi的建设值,此后基地的级别每提高一级,建设值将除以T并下取整(整除)。
现给定N、M、K、T、A[]和B[],小Hi需要你帮助他计算他完成基地建设的最小成本。
输入
输入包含多组测试数据。
输入的第一行为一个整数Q,表示测试数据的组数。
每组测试数据的第一行为4个整数N、M、K和T,意义如前文所述。
接下来的一行为M个整数,分别表示A1~AM。
接下来的一行为M个整数,分别表示B1~BM。
对于100%的数据,满足1<=N<=10,1<=M<=100,1<=K,T<=104。
对于100%的数据,满足Ai和Bi均为32位整型范围内的正整数。
对于100%的数据,满足1<=Q<=10。
输出
对于每组测试数据,如果小Hi最终能够完成基地建设,则输出小Hi完成基地建设所需要的最小成本,否则输出“No Answer”。
样例输入
2
2 2 2 2
1 3
1 2
2 2 2 2
1 2
1 1
样例输出
8
No Answer
题意有点绕,想清楚是完全背包问题以后还是比较简单的。
AC代码:
#include<cstdio>
#include<algorithm>
#define INF 1<<30
using namespace std;
typedef long long ll;
int main()
{
int Q,N,M,K,T;
int a[110],b[110];
ll dp[10010];
//dp[i]表示价值为i时的最小成本
while(~scanf("%d",&Q))
{
while(Q--)
{
ll res=0;
scanf("%d%d%d%d",&N,&M,&K,&T);
for(int i=1;i<=M;i++) scanf("%d",&a[i]);
for(int i=1;i<=M;i++) scanf("%d",&b[i]);
for(int u=1;u<=N;u++)
{
for(int i=1;i<10010;i++) dp[i]=INF;
dp[0]=0;
for(int i=1;i<=M;i++)
{
for(int j=0;j<=K;j++)
{
if(j+b[i]>K) dp[K]=min(dp[K],dp[j]+a[i]);
else dp[j+b[i]]=min(dp[j+b[i]],dp[j]+a[i]);
}
}
res+=dp[K];
//将每级累加
for(int v=1;v<=M;v++) b[v]/=T;
}
if(res>=INF) puts("No Answer");
else printf("%lld\n",res);
}
}
return 0;
}题目4 : 舰队游戏
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi最近在玩一款组建舰队出海进行战争的游戏,在这个游戏中,小Hi需要根据需要组建一只舰队,一支舰队里最多同时存在N艘舰船,每艘舰船最多同时装备M个装备。
在一次关卡中,小Hi希望能够组建一只仅由航母构成的舰队,这意味着所有舰船的装备都是某种类型的飞机,小Hi将要使用的飞机有两种类型:对空飞机和对舰飞机,顾名思义,对空飞机用于和敌对舰船搭载的飞机进行对抗,而对舰飞机则直接用于攻击敌对舰船本身。
每艘航母的M个装备栏位是不一样的,我们可以用“搭载量”来对其进行量化描述,有些装备栏位的搭载量较高,有些装备栏位的搭载量较低,对于第i艘舰船,我们用Ai,j表示其第j个装备栏位的搭载量。
小Hi的军备库里有T架飞机,我们Bi表示第i架飞机的对空攻击力,并用Ci表示第i架飞机的对舰攻击力,其中对空飞机的对舰攻击力为0,对舰飞机的对空攻击力为0。
为舰船装备飞机,会提高舰队的“制空值”和“伤害值”。舰队的制空值为所有飞机的对空攻击力与其对应的装备栏位的搭载量的乘积之和,即:
制空值=
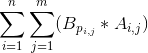
其中pi,j表示放置在第i艘舰船的第j个装备栏位的飞机编号。同理,舰队的伤害值为所有飞机的对舰攻击力与其对应的装备栏位的搭载量的乘积之和,即
伤害值=
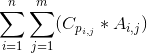
为了能够顺利的通过关卡,小Hi需要使得舰队的制空值不低于一个给定的值S,并且希望在这个条件下舰队的伤害值越高越好,这样能够尽量减少舰队的损耗。
同时,由于一艘舰船至少要装备一架对舰飞机才能够在炮击战中发动攻击,所以小Hi也好奇是否存在在满足制空值限制且伤害值最高的情况下,同时满足每一艘舰船至少装备一架对舰飞机。
而这个问题,就有待你来进行计算了~
输入
输入第一行为一个正整数Q,表示测试数据的组数。
在每组测试数据的第一行,为4个正整数N、M、T和S,意义如之前所述。
第2行~第n+1行,每行m个正整数,对应矩阵A。
第n+2行,为T个正整数B1 .. BT。
第n+3行,为T个正整数C1 .. CT。
对于30%的数据,满足N<=2,M<=2,T<=20,Q<=100。
对于剩下70%的数据,满足N<=4,M<=4,T<=1000,Q<=3。
对于100%的数据,满足1<=Ai,j, Bi, Ci <= 1000,0<= S <= 108。
输出
对于每组测试数据,如果存在满足制空值限制的方案的话,则首先在第一行输出在满足制空值限制下能够达到的最大攻击力D,在第二行中,如果在满足制空值限制且伤害值最高的情况下,能够同时满足每一艘舰船至少装备一架对舰飞机,则输出Yes,否则输出No。
如果不存在满足制空值限制的方案的话,则输出一行Not Exist。
样例输入
3
1 2 1 38
4 5
0
5
1 2 8 7
1 4
0 3 2 0 0 2 0 0
5 0 0 3 3 0 3 4
2 1 4 29
5
3
0 4 3 0
1 0 0 3
样例输出
Not Exist
5
Yes
0
No
对值直接从小到大排序,然后就是枚举状态贪心计算。
AC代码:
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int const MAX=1e3+5;
int N,M,T,S;
int sz_a;
int sz_b;
//对空飞机的数量
int sz_c;
//对舰飞机的数量
int b[MAX],B[MAX],c[MAX],C[MAX];
struct A
{
int num,pos;
}a[5][5],temp[20];
bool cmp(A x,A y)
{
return x.num>y.num;
}
//计算对空值
int cal_air(int k)
{
memset(temp,0,sizeof(temp));
sz_a=0;
//搭载了多少架对空飞机
for(int i=0;i<N;i++)
{
for(int j=0;j<M;j++)
{
if(k&(1<<(i*M+j)))
{
temp[sz_a++].num=a[i][j].num;
}
}
}
sort(temp,temp+sz_a,cmp);
int res=0;
for(int i=0,j=0;i<sz_a&&j<sz_b;i++,j++) res+=temp[i].num*B[j];
return res;
}
//计算对舰值
int cal_ship(int k)
{
memset(temp,0,sizeof(temp));
sz_a=0;
//搭载了多少架对舰飞机
for(int i=0;i<N&&sz_a<=sz_c;i++)
{
for(int j=0;j<M&&sz_a<=sz_c;j++)
{
if(!(k&(1<<(i*M+j))))
//如果已经搭载了对空飞机就不能搭载对舰飞机
{
temp[sz_a].num=a[i][j].num;
temp[sz_a++].pos=a[i][j].pos;
//后面还要用到舰艇的信息
}
}
}
sort(temp,temp+sz_a,cmp);
int res=0;
for(int i=0,j=0;i<sz_a&&j<sz_c;i++,j++) res+=temp[i].num*C[j];
return res;
}
//计算能不能满足每一艘舰船至少装备一架对舰飞机
bool judge_ship()
{
//枚举每一艘舰艇
for(int i=0;i<N;i++)
{
bool flag=false;
for(int j=0;j<M&&!flag;j++)
{
for(int k=0;k<min(sz_a,sz_c)&&!flag;k++)
{
if(((1<<(i*M+j))&temp[k].pos)) flag=true;
}
}
if(!flag) return false;
}
return true;
}
int main()
{
int Q;
scanf("%d",&Q);
while(Q--)
{
sz_b=0;
sz_c=0;
scanf("%d%d%d%d",&N,&M,&T,&S);
for(int i=0;i<N;i++)
{
for(int j=0;j<M;j++)
{
scanf("%d",&a[i][j].num);
a[i][j].pos=(1<<(i*M+j));
}
}
for(int i=0;i<T;i++)
{
scanf("%d",&b[i]);
if(b[i]) B[sz_b++]=b[i];
}
for(int i=0;i<T;i++)
{
scanf("%d",&c[i]);
if(c[i]) C[sz_c++]=c[i];
}
sort(B,B+sz_b,greater<int>());
sort(C,C+sz_c,greater<int>());
int ans=-1,tot=1<<(N*M);
// N艘舰船,每艘舰船M个装备,每个装备有装载和未装载两种情况,一共枚举2*n*m种可能
bool has=false;
for(int i=0;i<tot;i++)
{
if(cal_air(i)>=S)
{
int temp=cal_ship(i);
if(temp>ans||(temp==ans&&!has))
{
ans=temp;
has=judge_ship();
}
}
}
if(ans==-1) printf("Not Exist\n");
else printf("%d\n%s\n",ans,has?"Yes":"No");
}
}