hdu 3127 WHUgirls(二维背包）

WHUgirls

Time Limit: 3000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 2098    Accepted Submission(s): 796

Problem Description

There are many pretty girls in Wuhan University, and as we know, every girl loves pretty clothes, so do they. One day some of them got a huge rectangular cloth and they want to cut it into small rectangular pieces to make scarves. But different girls like different style, and they voted each style a price wrote down on a list. They have a machine which can cut one cloth into exactly two smaller rectangular pieces horizontally or vertically, and ask you to use this machine to cut the original huge cloth into pieces appeared in the list. Girls wish to get the highest profit from the small pieces after cutting, so you need to find out a best cutting strategy. You are free to make as many scarves of a given style as you wish, or none if desired. Of course, the girls do not require you to use all the cloth.

 

Input

The first line of input consists of an integer T, indicating the number of test cases.
The first line of each case consists of three integers N, X, Y, N indicating there are N kinds of rectangular that you can cut in and made to scarves; X, Y indicating the dimension of the original cloth. The next N lines, each line consists of two integers, xi, yi, ci, indicating the dimension and the price of the ith rectangular piece cloth you can cut in.

 

Output

Output the maximum sum of prices that you can get on a single line for each case.

Constrains
0 < T <= 20
0 <= N <= 10; 0 < X, Y <= 1000
0 < xi <= X; 0 < yi <= Y; 0 <= ci <= 1000

 

Sample Input

   
   
   
   

    
    
    
    1
2 4 4
2 2 2
3 3 9
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    9
   
   
   
   

 

参考了http://blog.csdn.net/lulipeng_cpp/article/details/7587465

看了半天才看懂，太菜了。

我再根据我的理解补充一下。

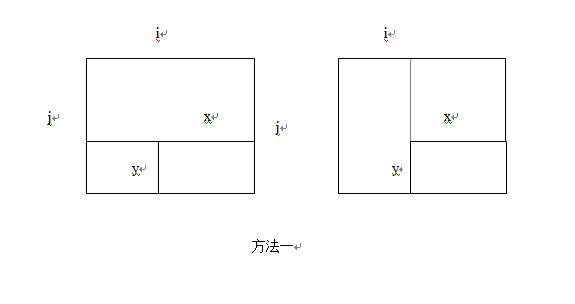
方法一的第一种方案

dp[i][j-y]为上面最大的矩形的价值，dp[i-x][y]为左下矩形的价值，就是与它等大的矩形的价值，所以总价值为dp[i][j-y]+dp[i-x][y]+c。其他方案也类似，就不一一解释了。

代码:

//421ms
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=1000+100;
int a[maxn];
int b[maxn];
int c[maxn];
int dp[maxn][maxn];
int max(int a,int b,int c)
{
    a=a>b?a:b;
    return a>c?a:c;
}
int main()
{
    int n,x,y,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d",&n,&x,&y);
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d%d",&a[i],&b[i],&c[i]);
        }
        memset(dp,0,sizeof(dp));
        for(int i=0;i<=x;i++)
        {
            for(int j=0;j<=y;j++)
            {
                for(int k=1;k<=n;k++)
                {
                    if(i>=a[k]&&j>=b[k])
                    {
                        dp[i][j]=max(dp[i][j],dp[i-a[k]][j]+dp[a[k]][j-b[k]]+c[k],dp[i][j-b[k]]+dp[i-a[k]][b[k]]+c[k]);
                    }
                    if(i>=b[k]&&j>=a[k])
                    {
                        dp[i][j]=max(dp[i][j],dp[i-b[k]][j]+dp[b[k]][j-a[k]]+c[k],dp[i][j-a[k]]+dp[i-b[k]][a[k]]+c[k]);
                    }
                }
            }
        }
        printf("%d\n",dp[x][y]);
    }
    return 0;
}