Poj1696计算几何的叉积+极角排序+贪心

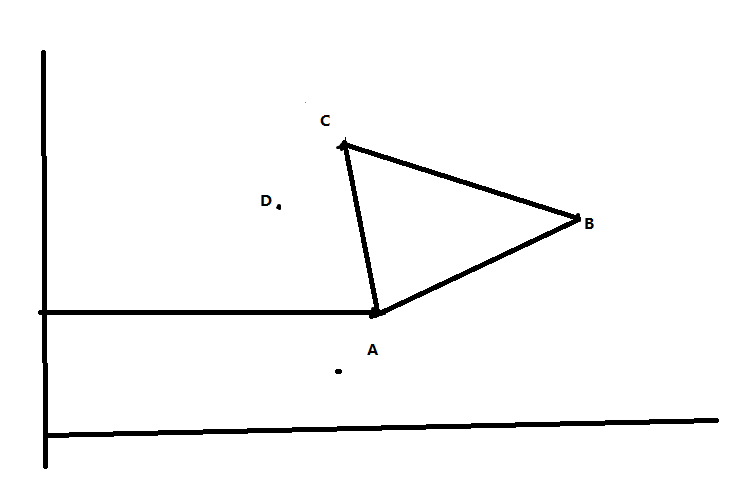
  说下当时自己的证明（后来有人说这是个所谓极角排序问题，Anyway思路差不多，有点贪心意思，顺带考察了叉积应用），问题可以归结为如果这个虫来到点A，它应该选择的下一个plant的点的原则是？

  我们可以证明如果点A能够经点B，左转到点C，那么点A就应该选择跳到点B。

  证明:

   主要证明从点A跳到点B，虫子可以选择的后续点比跳到点C更加多。

  (1 )   如果点A跳到点C，那么点B就无法再到达。但是跳到点B，却可以再跳到点C. 所以从A 到点B的路径至少比从A跳到C的路径多了一个B。

  (2） 点A跳到点C，后面所有可能的可以跳到的点，比如点D，从点A跳到点B后，也一样可以到达。证明：点D在边AC的左侧，边AC在AB的左侧，所以点D也在AB的左侧，所以点D可以从B到达。

  由此我们可以定义一个 点极角大小关系 B >a C （如果点A能从点B到点C）。 至于如何从程序判断，就一个简单的叉积 BA * CA ，如果大于0，说明边BA左转到边CA，B >a C.

  所以问题的算法最终变成了：从规定的第一个y值最小的点A开始，不断找后面对于当前点A的极角最大的点B（就一个排序）。

 

 

#include <iostream>
#include<stdio.h>
#include <cmath>
#include <algorithm>
using namespace std;

class Point
{
public:
	Point(double tmpx,double tmpy,double tId)
	{
		x=tmpx;
		y=tmpy;
		id=tId;
	}
	Point(double tmpx,double tmpy)
	{
		x=tmpx;
		y=tmpy;
	}
	Point()
	{
		x=0.0f;
		y=0.0f;
	}

	double x,y;
	int id;
};

//Returen (p2-p1)*(p3-p1)
double CrossProduct(Point point1,Point point2,Point point3)
{
	Point vec1=Point(point1.x-point3.x,point1.y-point3.y);
	Point vec2=Point(point2.x-point3.x,point2.y-point3.y);

	return (vec1.x*vec2.y-vec1.y*vec2.x);
}


double Distance(Point p1,Point p2)
{
	//double dis=abs(p1.x-p2.x)+abs(p1.y-p2.y);
	double dis=sqrt(pow(p1.x-p2.x,2) + pow(p1.y-p2.y,2) );
	return dis;
}

Point currentPoint;

//See if p1 can reach p2 starting from p3, or reverse
//If p1>p2 (p1 can reach p2 through p3), return 1;else return -1;
bool PointReachable(Point point1, Point point2)
{
	double d = CrossProduct(point1,point2, currentPoint);
	if(d>0)//p1 reach p2,p1 is better
	{
		return true;
	}
	else if(d<0)
	{
		return false;
	}
	else// p1,p2,p3 are in the same line.
	{
		double dis1=Distance(point1,currentPoint);
		double dis2=Distance(point2,currentPoint);
		if(dis1<dis2)
			return true;
		else
			return false;
	}
}

int main()
{
	int iCases=0;
	Point plantPoints[60];
	Point sortedPoints[60][60];
	scanf("%d",&iCases);
	while(iCases>0)
	{
		int iPoints=0;
		scanf("%d",&iPoints);
		double minx=(double)(1<<30);
		double minY=(double)(1<<30);
		int firstIndex=-1;
		for(int i=1;i<=iPoints;i++)
		{
			int tmpi;
			scanf("%d",&tmpi);
			scanf("%lf%lf",&plantPoints[tmpi].x,&plantPoints[tmpi].y);
			plantPoints[tmpi].id=tmpi;
			if(plantPoints[tmpi].y<=minY)
			{
				if(plantPoints[tmpi].y<minY || plantPoints[tmpi].x<minx)
				{
					minY=plantPoints[tmpi].y;
					minx=plantPoints[tmpi].x;
					firstIndex=tmpi;
				}
			}
		}

		//Swap
		Point tmpPoint=plantPoints[1];
		plantPoints[1]=plantPoints[firstIndex];
		plantPoints[firstIndex]=tmpPoint;


		printf("%d %d",iPoints,firstIndex);
		currentPoint=plantPoints[1];
		//Find plantPoints[i]'s best next point.
		for(int i=2;i<iPoints;i++)
		{
			sort(plantPoints+i,plantPoints+iPoints+1,PointReachable);
			currentPoint=plantPoints[i];
			printf(" %d",plantPoints[i].id);
		}
		if(iPoints>1)
			printf(" %d",plantPoints[iPoints].id);
		printf("\n");
		
		iCases--;
	}
	return 0;
}